一看就懂的信息熵

信息熵：

（看之前可以了解一下信息熵的创始人：克劳德·艾尔伍德·香农（Claude Elwood Shannon ，1916年4月30日—2001年2月24日））

先给出信息熵的公式：

                                           

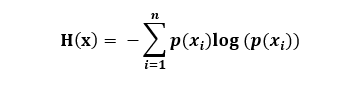
其中：𝑝(𝑥_𝑖)代表随机事件𝑥_𝑖的概率。
下面逐步介绍信息熵公式来源！

首先了解一下信息量：信息量是对信息的度量，就跟时间的度量是秒一样，当我们考虑一个离散的随机变量 x 的时候，当我们观察到的这个变量的一个具体值的时候，我们接收到了多少信息呢？

多少信息用信息量来衡量，我们接受到的信息量跟具体发生的事件有关。

信息的大小跟随机事件的概率有关。越小概率的事情发生了产生的信息量越大，如湖南产生 的地震了；越大概率的事情发生了产生的信息量越小，如太阳从东边升起来了（肯定发生嘛， 没什么信息量）。这很好理解！

因此一个具体事件的信息量应该是随着其发生概率而递减的，且不能为负。但是这个表示信 息量函数的形式怎么找呢？随着概率增大而减少的函数形式太多了！不要着急，我们还有下 面这条性质。

如果我们有俩个不相关的事件 x 和 y，那么我们观察到的俩个事件同时发生时获得的信息应 该等于观察到的事件各自发生时获得的信息之和，即： h(x,y) = h(x) + h(y)

由于 x，y 是俩个不相关的事件，那么满足 p(x,y) = p(x)*p(y).

根据上面推导，我们很容易看出 h(x)一定与 p(x)的对数有关（因为只有对数形式的真数相乘 之后，能够对应对数的相加形式，可以试试）。因此我们有信息量公式如下：

𝐡(𝐱) = −𝒍𝒐𝒈_𝟐𝒑(𝒙)

（1）为什么有一个负号？其中，负号是为了确保信息一定是正数或者是 0，总不能为负数吧！

（2）为什么底数为 2 这是因为，我们只需要信息量满足低概率事件 x 对应于高的信息量。那么对数的选择是任意的。我们只是遵循信息论的普遍传统，使用 2 作为对数的底！ 

信息熵 下面正式引出信息熵：信息量度量的是一个具体事件发生了所带来的信息，而熵则是在结果出来之前对可能产生的信息量的期望——考虑该随机变量的所有可能取值，即所有可能发生事件所带来的信息量的期望。即

𝐇(𝐱) = −𝒔𝒖𝒎(𝒑(𝒙)𝒍𝒐𝒈_𝟐𝒑(𝒙))

转换一下也就是：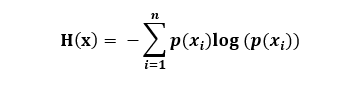


最终我们的公式来源推导完成了。

信息熵还可以作为一个系统复杂程度的度量，如果系统越复杂，出现不同情况的种类越多， 那么他的信息熵是比较大的。如果一个系统越简单，出现情况种类很少（极端情况为 1 种情况，那么对应概率为 1，那么对应的信息熵为 0），此时的信息熵较小。

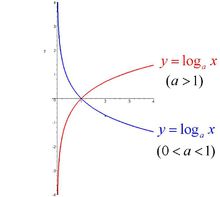
最后附上对数函数一些性质，你画出 𝐟(𝐱) = −𝒍𝒐𝒈_𝟐𝒙 的图像会更加明了。 

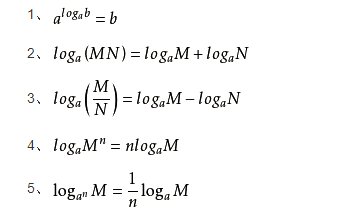
链接：https://www.zhihu.com/question/22178202/answer/161732605

来源：知乎