AC日记——【模板】最小费用最大流 P3381

题目描述

如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入输出格式

输入格式：

 

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含四个正整数ui、vi、wi、fi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi），单位流量的费用为fi。

 

输出格式：

 

一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。

 

输入输出样例

输入样例#1：

4 5 4 3
4 2 30 2
4 3 20 3
2 3 20 1
2 1 30 9
1 3 40 5

输出样例#1：

50 280

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=5000，M<=50000

样例说明：

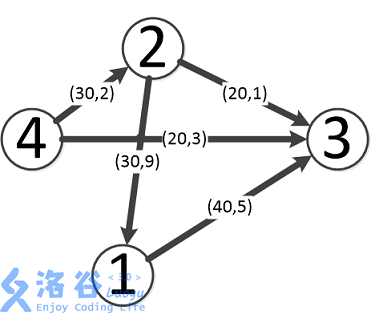
如图，最优方案如下：

第一条流为4-->3，流量为20，费用为3*20=60。

第二条流为4-->2-->3，流量为20，费用为（2+1）*20=60。

第三条流为4-->2-->1-->3，流量为10，费用为（2+9+5）*10=160。

故最大流量为50，在此状况下最小费用为60+60+160=280。

故输出50 280。

 

思路：

　　裸费用流：

　　唯一优化：先不建反向边，当用到反向边时才建；

 

来，上代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define maxn 5005
#define maxm 100005
#define INF 0x7ffffff

using namespace std;

int n,m,s,t,V[maxm],F[maxm],E[maxm],W[maxm],cnt=1;
int head[maxn],dis[maxn],pre[maxn],U[maxm],maxflow,cost;

bool if_[maxn];

char Cget;

inline void in(int &now)
{
    now=0,Cget=getchar();
    while(Cget>'9'||Cget<'0') Cget=getchar();
    while(Cget>='0'&&Cget<='9')
    {
        now=now*10+Cget-'0';
        Cget=getchar();
    }
}

bool spfa()
{
    int que[maxm],h=0,tail=1;
    for(int i=1;i<=n;i++) dis[i]=INF,pre[i]=-1;
    dis[s]=0,if_[s]=true,que[0]=s;
    while(h<tail)
    {
        int now=que[h++];
        for(int i=head[now];i;i=E[i])
        {
            if(F[i]&&dis[V[i]]>dis[now]+W[i])
            {
                dis[V[i]]=dis[now]+W[i],pre[V[i]]=i;
                if(!if_[V[i]])
                {
                    if_[V[i]]=true;
                    que[tail++]=V[i];
                }
            }
        }
        if_[now]=false;
    }
    return dis[t]<INF;
}

int main()
{
    in(n),in(m),in(s),in(t);
    int v,f,w,u;
    while(m--)
    {
        in(u),in(v),in(f),in(w);
        V[++cnt]=v,F[cnt]=f,W[cnt]=w;
        U[cnt]=u,E[cnt]=head[u],head[u]=cnt++;
    }
    while(spfa())
    {
        int now=t,pos=INF;
        while(pre[now]!=-1)
        {
            if(F[pre[now]]<pos) pos=F[pre[now]];
            now=U[pre[now]];
        }
        now=t;
        while(pre[now]!=-1)
        {
            F[pre[now]]-=pos;
            if(!V[pre[now]^1])
            {
                V[pre[now]^1]=U[pre[now]];
                U[pre[now]^1]=V[pre[now]];
                W[pre[now]^1]=-W[pre[now]];
                E[pre[now]^1]=head[V[pre[now]]];
                head[V[pre[now]]]=pre[now]^1;
            }
            F[pre[now]^1]+=pos;
            now=U[pre[now]];
        }
        maxflow+=pos,cost+=pos*dis[t];
    }
    cout<<maxflow<<' '<<cost;
    return 0;
}