AC日记——Sign on Fence Codeforces 484e

E. Sign on Fence

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Bizon the Champion has recently finished painting his wood fence. The fence consists of a sequence of n panels of 1 meter width and of arbitrary height. The i-th panel's height is hi meters. The adjacent planks follow without a gap between them.

After Bizon painted the fence he decided to put a "for sale" sign on it. The sign will be drawn on a rectangular piece of paper and placed on the fence so that the sides of the sign are parallel to the fence panels and are also aligned with the edges of some panels. Bizon the Champion introduced the following constraints for the sign position:

1. The width of the sign should be exactly w meters.
2. The sign must fit into the segment of the fence from the l-th to the r-th panels, inclusive (also, it can't exceed the fence's bound in vertical direction).

The sign will be really pretty, So Bizon the Champion wants the sign's height to be as large as possible.

You are given the description of the fence and several queries for placing sign. For each query print the maximum possible height of the sign that can be placed on the corresponding segment of the fence with the given fixed width of the sign.

Input

The first line of the input contains integer n — the number of panels in the fence (1 ≤ n ≤ 105).

The second line contains n space-separated integers hi, — the heights of the panels (1 ≤ hi ≤ 109).

The third line contains an integer m — the number of the queries (1 ≤ m ≤ 105).

The next m lines contain the descriptions of the queries, each query is represented by three integers l, r and w (1 ≤ l ≤ r ≤ n,1 ≤ w ≤ r - l + 1) — the segment of the fence and the width of the sign respectively.

Output

For each query print the answer on a separate line — the maximum height of the sign that can be put in the corresponding segment of the fence with all the conditions being satisfied.

Examples

input

5
1 2 2 3 3
3
2 5 3
2 5 2
1 5 5

output

2
3
1

Note

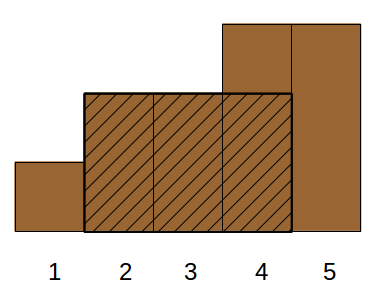
The fence described in the sample looks as follows:

The possible positions for the signs for all queries are given below.

The optimal position of the sign for the first query.The optimal position of the sign for the second query.The optimal position of the sign for the third query.

 

思路：

　　其实这题不水。

　　我们考虑主席树；

　　这个就变水了；

　　我们离散一下高度；

　　然后针对每个离散后的高度建立有n个节点的线段树；

　　线段树的末节点表示当前节点的高度是否大于当前离散的高度（不懂请看代码）；

　　然后维护最大子段；

　　然后，每次二分高度，判断以当前高度的根的树高度是否在l~r区间满足w宽度；

　　然后，轻松ac（不知道wa了多少次）；

 

来，上代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define maxn 100005

using namespace std;

struct SequenceNodeType {
    int p,hi;
};
struct SequenceNodeType point[maxn];

struct TreeNodeType {
    int lc,rc,dis,ld,rd,size;
};
struct TreeNodeType tree[maxn*50];

struct AnsType {
    int l,r,dis,size;
    
    AnsType(int l_,int r_,int dis_,int size_)
    {
        l=l_,r=r_,dis=dis_,size=size_;
    }
};

int if_z,n,hash[maxn],size,Pre,tot;
int li,ri,ans,x,m,root[maxn];

char Cget;

inline void in(int &now)
{
    now=0,if_z=1,Cget=getchar();
    while(Cget>'9'||Cget<'0')
    {
        if(Cget=='-') if_z=-1;
        Cget=getchar();
    }
    while(Cget>='0'&&Cget<='9')
    {
        now=now*10+Cget-'0';
        Cget=getchar();
    }
    now*=if_z;
}

bool icmp(int a,int b)
{
    return a>b;
}

bool cmp(SequenceNodeType a,SequenceNodeType b)
{
    return a.hi>b.hi;
}

void tree_build(int &now,int l,int r)
{
    now=++tot;
    tree[now].size=r-l+1;
    if(l==r) return ;
    int mid=(l+r)>>1;
    tree_build(tree[now].lc,l,mid);
    tree_build(tree[now].rc,mid+1,r);
}

void tree_add(int pre,int &now,int to,int l,int r)
{
    now=++tot;
    tree[now].size=tree[pre].size;
    if(l==r)
    {
        tree[now].dis=1,tree[now].rd=1,tree[now].ld=1;
        return ;
    }
    int mid=(l+r)>>1;
    if(to>mid)
    {
        tree_add(tree[pre].rc,tree[now].rc,to,mid+1,r);
        tree[now].lc=tree[pre].lc;
    }
    else
    {
        tree_add(tree[pre].lc,tree[now].lc,to,l,mid);
        tree[now].rc=tree[pre].rc;
    }
    tree[now].dis=tree[tree[now].lc].rd+tree[tree[now].rc].ld;
    tree[now].dis=max(tree[now].dis,tree[tree[now].lc].dis);
    tree[now].dis=max(tree[now].dis,tree[tree[now].rc].dis);
    if(tree[tree[now].lc].ld==tree[tree[now].lc].size)
    {
        tree[now].ld=tree[tree[now].lc].size+tree[tree[now].rc].ld;
    }
    else tree[now].ld=tree[tree[now].lc].ld;
    if(tree[tree[now].rc].rd==tree[tree[now].rc].size)
    {
        tree[now].rd=tree[tree[now].rc].size+tree[tree[now].lc].rd;
    }
    else tree[now].rd=tree[tree[now].rc].rd;
}

struct AnsType tree_query(int now,int l,int r,int tl,int tr)
{
    if(l==tl&&r==tr)
    {
        AnsType pos(tree[now].ld,tree[now].rd,tree[now].dis,tree[now].size);
        return pos;
    }
    int mid=(l+r)>>1;
    if(tl>mid) return tree_query(tree[now].rc,mid+1,r,tl,tr);
    else if(tr<=mid) return tree_query(tree[now].lc,l,mid,tl,tr);
    else
    {
        AnsType pos(0,0,0,0);
        AnsType ll=tree_query(tree[now].lc,l,mid,tl,mid);
        AnsType rr=tree_query(tree[now].rc,mid+1,r,mid+1,tr);
        pos.size=ll.size+rr.size;
        pos.dis=max(ll.dis,rr.dis);
        pos.dis=max(pos.dis,ll.r+rr.l);
        if(ll.size==ll.l) pos.l=ll.size+rr.l;
        else pos.l=ll.l;
        if(rr.size==rr.r) pos.r=rr.size+ll.r;
        else pos.r=rr.r;
        return pos;
    }
}

bool check(int now)
{
    AnsType pos=tree_query(root[now],1,n,li,ri);
    int ans_=max(pos.dis,max(pos.l,pos.r));
    if(ans_>=x) return true;
    else return false;
}

int find(int pos)
{
    int l=1,r=size,mid;
    while(l<r)
    {
        mid=(l+r)>>1;
        if(hash[mid]==pos) return mid;
        if(pos>hash[mid]) r=mid-1;
        else l=mid+1;
    }
    return l;
}

int main()
{
    in(n);
    for(int i=1;i<=n;i++)
    {
        point[i].p=i;
        in(point[i].hi);
        hash[i]=point[i].hi;
    }
    sort(hash+1,hash+n+1,icmp);
    sort(point+1,point+n+1,cmp);
    size=unique(hash+1,hash+n+1)-hash-1;
    tree_build(root[0],1,n);Pre=root[0];
    for(int i=1;i<=n;i++)
    {
        int to=find(point[i].hi);
        tree_add(Pre,root[to],point[i].p,1,n);Pre=root[to];
    }
    in(m);
    while(m--)
    {
        in(li),in(ri),in(x);
        int mid,l=1,r=size;
        while(l<=r)
        {
            mid=(l+r)>>1;
            if(check(mid)) ans=mid,r=mid-1;
            else l=mid+1;
        }
        printf("%d\n",hash[ans]);
    }
    return 0;
}