AC日记——滑动窗口 洛谷 P1886

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

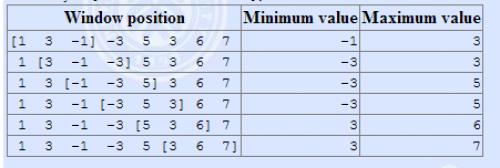
输入输出格式

输入格式：

 

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

 

输出格式：

 

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

 

输入输出样例

输入样例#1：

8 3
1 3 -1 -3 5 3 6 7

输出样例#1：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明

50%的数据，n<=10^5

100%的数据，n<=10^6

 

思路：

　　裸线段树；

 

来，上代码：

#include <cstdio>
#include <iostream>
#include <algorithm>

using namespace std;

class T_tree {
    public:
        int l,r,dis_max,dis_min,mid;
        
        void dis_()
        {
            scanf("%d",&dis_max);
            dis_min=dis_max;
        }
        
        void mid_()
        {
            mid=(l+r)>>1;
        }
};
class T_tree tree[4000001];

class T_ans {
    public:
        int minn,maxn;
};
class T_ans ans[1000001];

int n,k;

inline void tree_up(int now)
{
    tree[now].dis_max=max(tree[now<<1].dis_max,tree[now<<1|1].dis_max);
    tree[now].dis_min=min(tree[now<<1].dis_min,tree[now<<1|1].dis_min);
}

void tree_build(int now,int l,int r)
{
    tree[now].l=l,tree[now].r=r;
    if(l==r)
    {
        tree[now].dis_();
        return ;
    }
    tree[now].mid_();
    tree_build(now<<1,l,tree[now].mid);
    tree_build(now<<1|1,tree[now].mid+1,r);
    tree_up(now);
}

inline class T_ans ans_(int mi,int ma)
{
    class T_ans cur_;
    cur_.maxn=ma;
    cur_.minn=mi;
    return cur_;
}

class T_ans tree_query(int now,int l,int r)
{
    if(tree[now].l==l&&tree[now].r==r)
    {
        return ans_(tree[now].dis_min,tree[now].dis_max);
    }
    if(l>tree[now].mid) return tree_query(now<<1|1,l,r);
    else if(r<=tree[now].mid) return tree_query(now<<1,l,r);
    else
    {
        class T_ans A=tree_query(now<<1,l,tree[now].mid);
        class T_ans B=tree_query(now<<1|1,tree[now].mid+1,r);
        A.maxn=max(A.maxn,B.maxn);
        A.minn=min(A.minn,B.minn);
        return A;
    }
}

int main()
{
    scanf("%d%d",&n,&k);
    tree_build(1,1,n);
    for(int i=k;i<=n;i++)
    {
        ans[i-k+1]=tree_query(1,i-k+1,i);
    }
    for(int i=1;i<=n-k+1;i++)
    {
        printf("%d ",ans[i].minn);
    }
    printf("\n");
    for(int i=1;i<=n-k+1;i++)
    {
        printf("%d ",ans[i].maxn);
    }
    return 0;
}