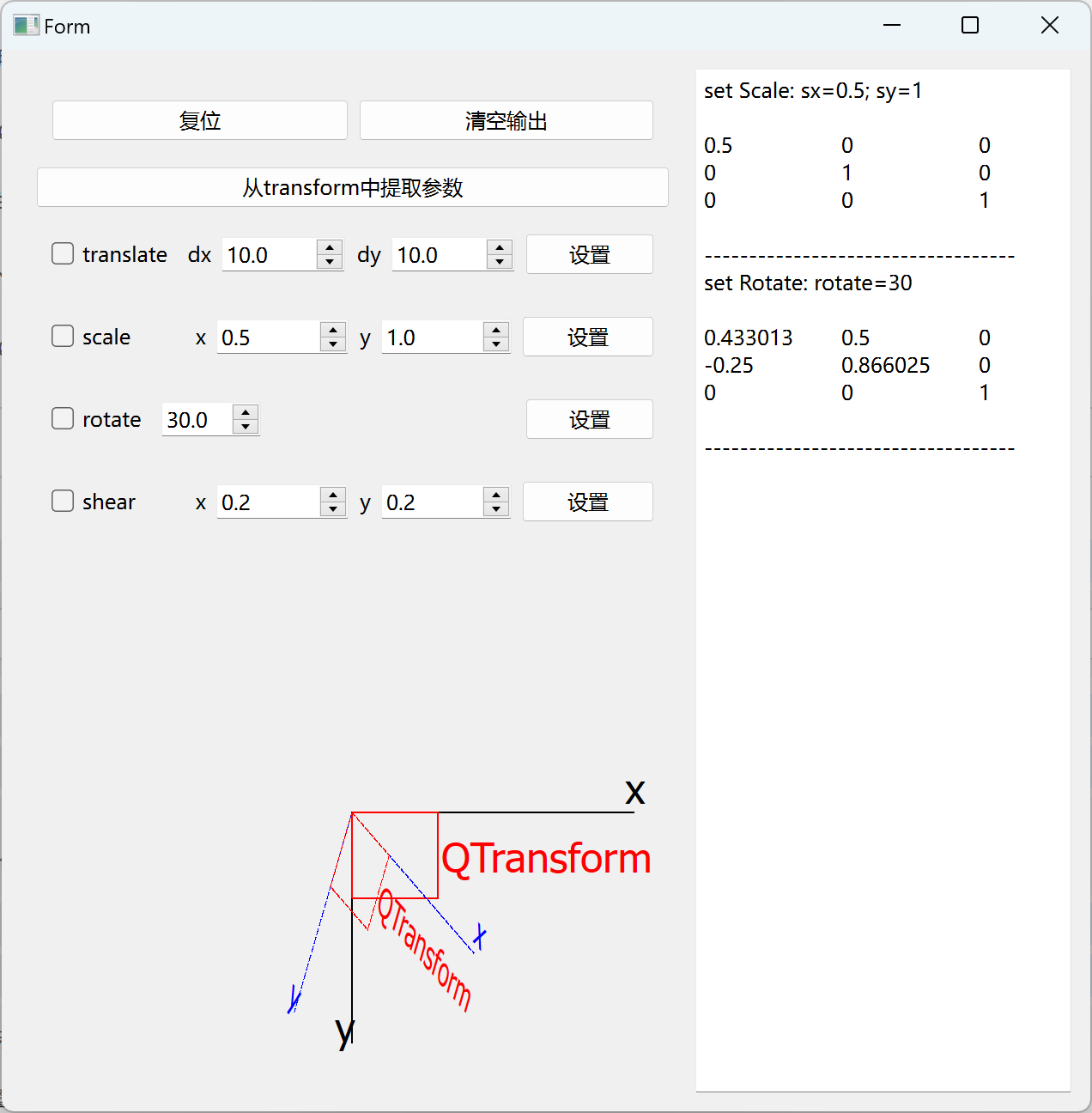
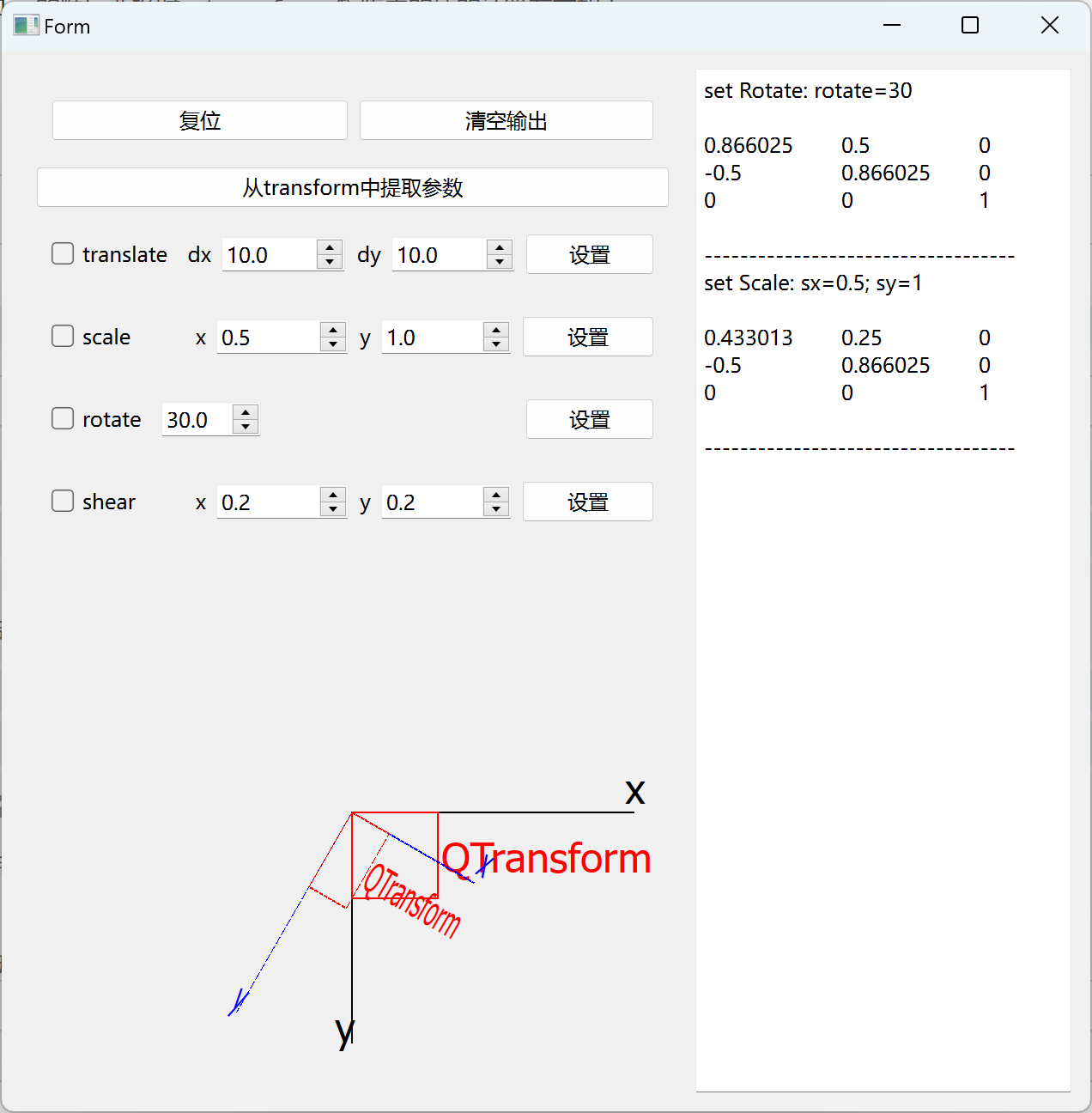
Qt 从 QTransform 逆向解出 Translate/Scale/Rotate(平移/缩放/旋转)分析
QTransform 用于图形绘制,它定义了如何平移(translate)、缩放(scale)、切变(shear)、旋转(rotate)或投射(project)坐标系。注意:QTransform 是作用于坐标系,不是直接作用于图形。实际运用中我们可以通过 QPainter 、 QGraphicsView、QGraphicsItem 实现图形的平移、缩放、旋转等操作,但是需要从当前图形对象中获取当前旋转的角度、缩放比例时无法找到合适的函数直接获取。有很多建议是从 QTransform 中获取,因为我们总是能通过 transform 获取到 QTransform ,而且QT帮助文档中也给出了对应矩阵的说明。通过实践发现
QTransform 的矩阵说明是指执行单一变换时矩阵中每个数值的含义,当执行了一系列的平移、缩放、旋转后,该矩阵已经经过多次运算,所包含的数值已经不是我们当时设置的值,也就是说这些值是平移、缩放、旋转相互作用后的数值。如果想得到当初我们设置的数值,就需要经过逆向的计算。
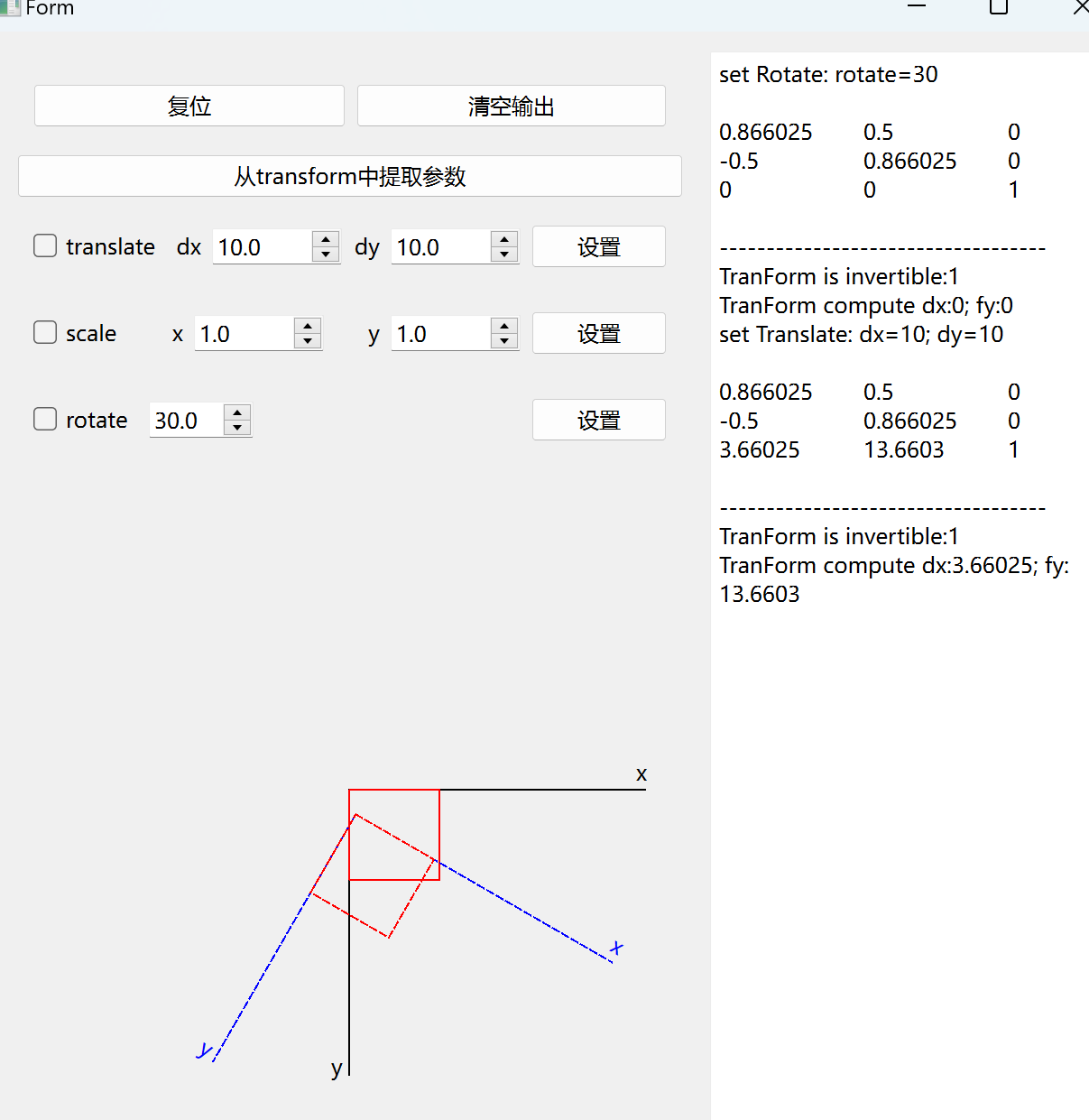
首先,我们需要了解 QTransform 矩阵是如何运算的。为了帮助我们快速了解矩阵的运算过程,我设计了一个小程序,每次平移、缩放、旋转后都会输出 QTransform 计算后的矩阵信息。参考项目地址
QTransform 的定义
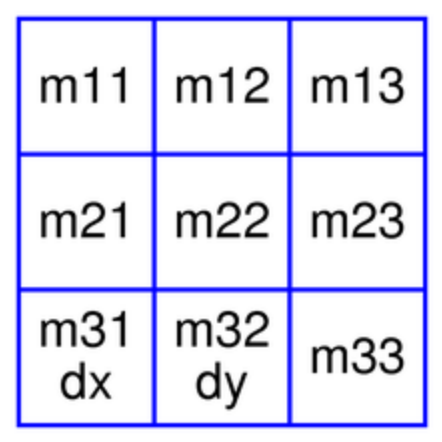
QTransform 只是定义了一个变换矩阵,实际的图形变换是由 QPainter 中的绘制程序来实现。QPainter 使用的标准坐标系是:以左上角为原点,X 轴向右,Y 轴向下。QTransform 对象包含一个 3 x 3 矩阵。m31 (dx) 、 m32 (dy) 表示水平与垂直位移。m11 、 m22 表示水平与垂直缩放比。m21 、 m12 表示水平与垂直切变。m13 、 m23 表示水平与垂直投影, m33 是投影因子。 3 x 3 矩阵如下图所示
平面上的一个点通过 QTransform 变换到另外一个点的计算公式如下, (x, y) 为原始点, (x', y')是变换后的点。
x' = m11*x + m21*y + dx
y' = m22*y + m12*x + dy
if (!isAffine()) {
w' = m13*x + m23*y + m33
x' /= w'
y' /= w'
}
对于一个恒等矩阵(identity matrix),m11、m22、m33 的值为 1,其它值为0。恒等矩阵作用于图形时不会产生任何变化。m12、m21 控制切变,它们会扭曲坐标系。坐标系的旋转(Rotation)是通过同时设置切变(Shear)和缩放(scale)来实现的。坐标系的透视(Perspective)是通过同时设置投影(projection)和缩放(scale)实现的。
很显然,当我们设置了缩放,又设置了旋转,m11、m22 就不再仅表示缩放,m12、m21 也不再仅表示切变。如果要得到原始值,需要经过计算。
Transform 计算与组合
1. Transform 计算
当我们执行如下代码时,最终的 transform 是如何计算出来的呢?
const double a = qDegreesToRadians(45.0);
double sina = sin(a);
double cosa = cos(a);
QTransform scale(0.5, 0, 0, 1.0, 0, 0);
QTransform rotate(cosa, sina, -sina, cosa, 0, 0);
QTransform translate(1, 0, 0, 1, 50.0, 50.0);
QTransform transform = scale * rotate * translate;
变量 scale 表示的矩阵为:
变量 rotate 表示的矩阵为: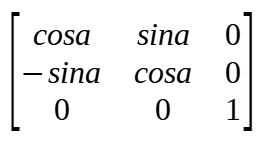
变量 translate 表示的矩阵为:
坐标系变换执行顺序如下:translate -> rotate -> scale
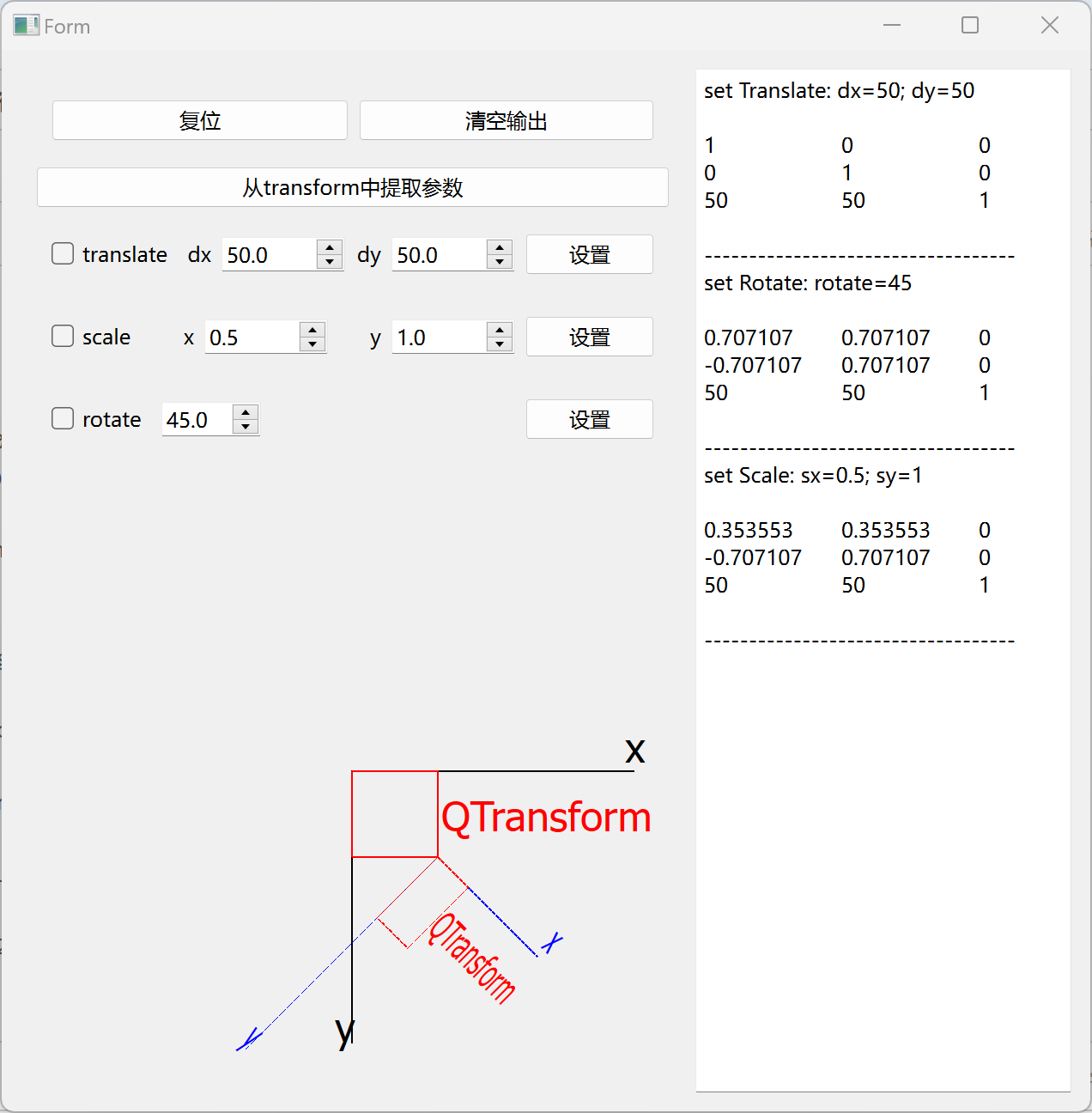
先计算 temp = rotate * translate:
再计算 transform = scale * temp : 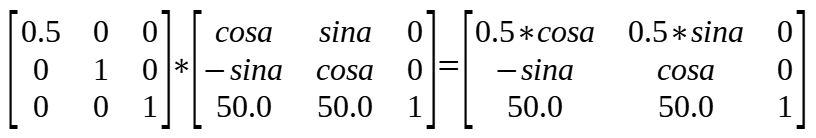
注意:后执行的变换在做矩阵乘法时要放在左边,即左乘
2. Transform 组合
坐标系的旋转会同时影响 m11 m12 m21 m22,坐标系透视会同时影响 m11 m13 m22 m23 m33,所以了解 Transform 的组合必须要了解坐标系的旋转与透视。我们可以先从看似互不影响的操作(实际顺序不同时产生影响)来看。
(1)translate 与 scale
当按照 translate -> scale 的顺序变换时,transform 矩阵中的值就是我们设置的值。
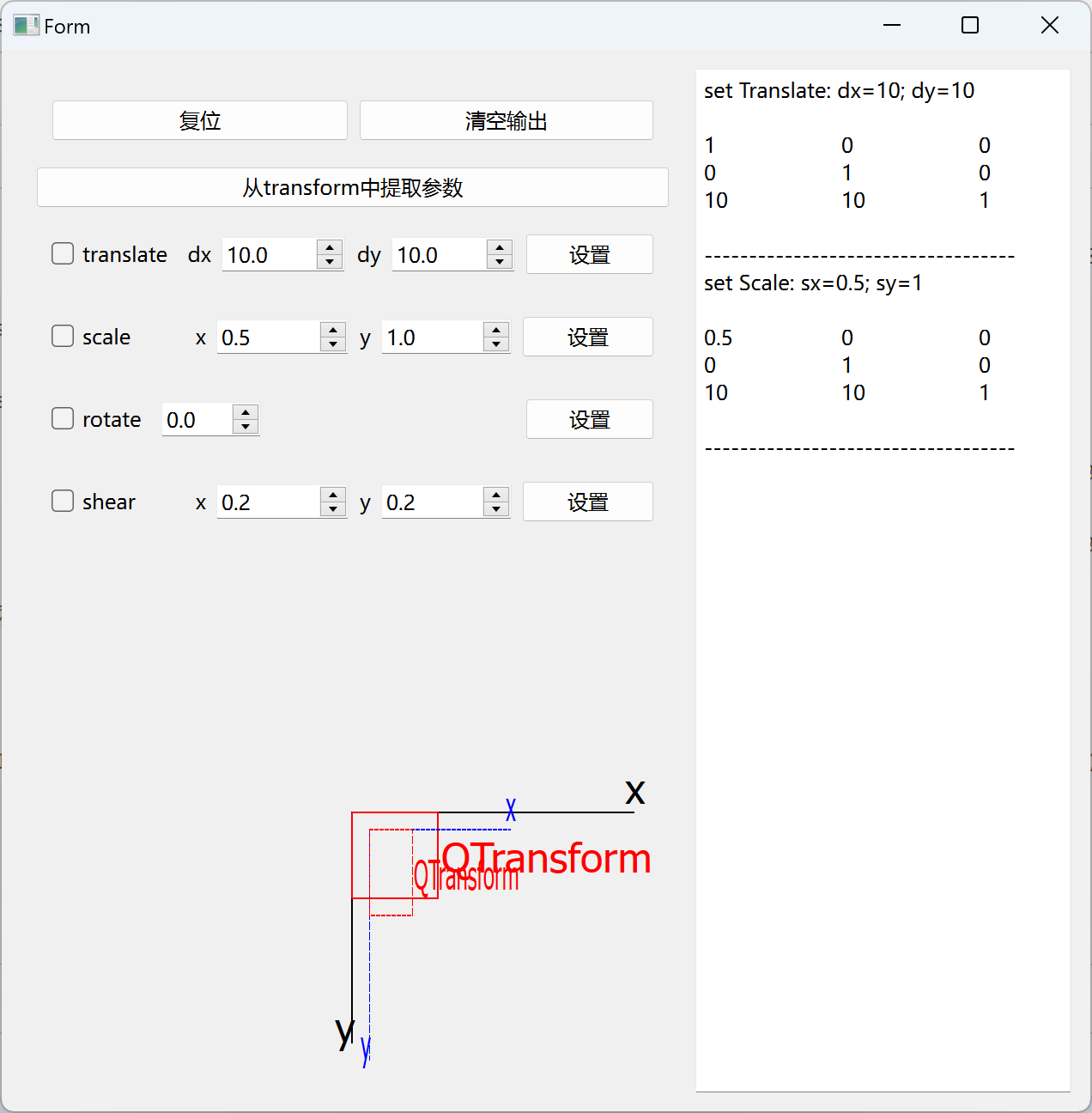
当安照 scale -> translate 的顺序变换时,transform 矩阵中dx dy的值受到 scale 的影响不再是我们设置的值。
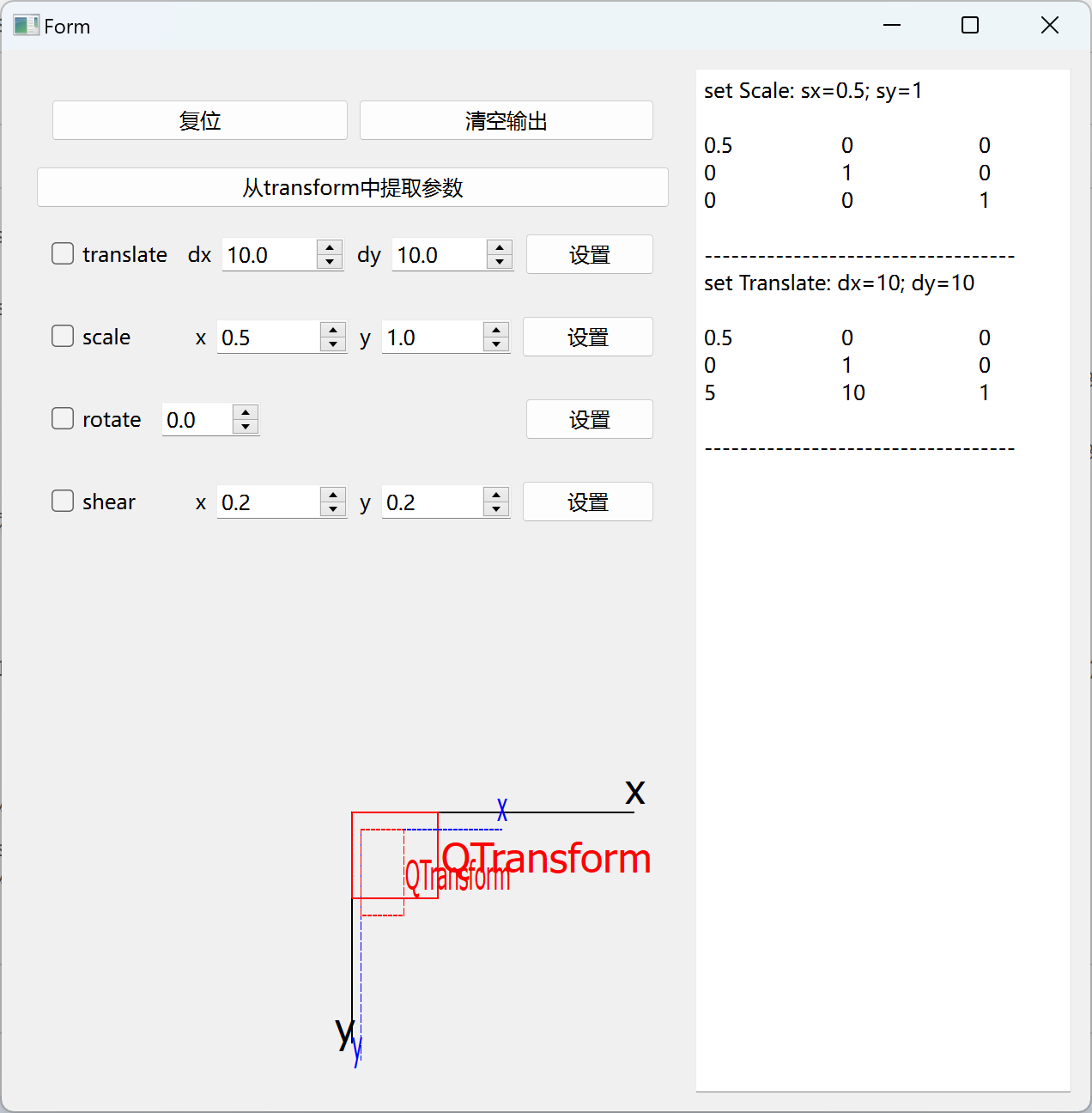
这跟前面讲的矩阵的运算顺序有关。
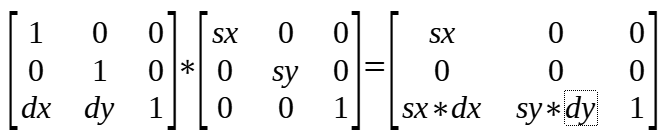
(2)translate 与 rotate
当按照 translate -> rotate的顺序变换时,transform 矩阵中的值就是我们设置的值。
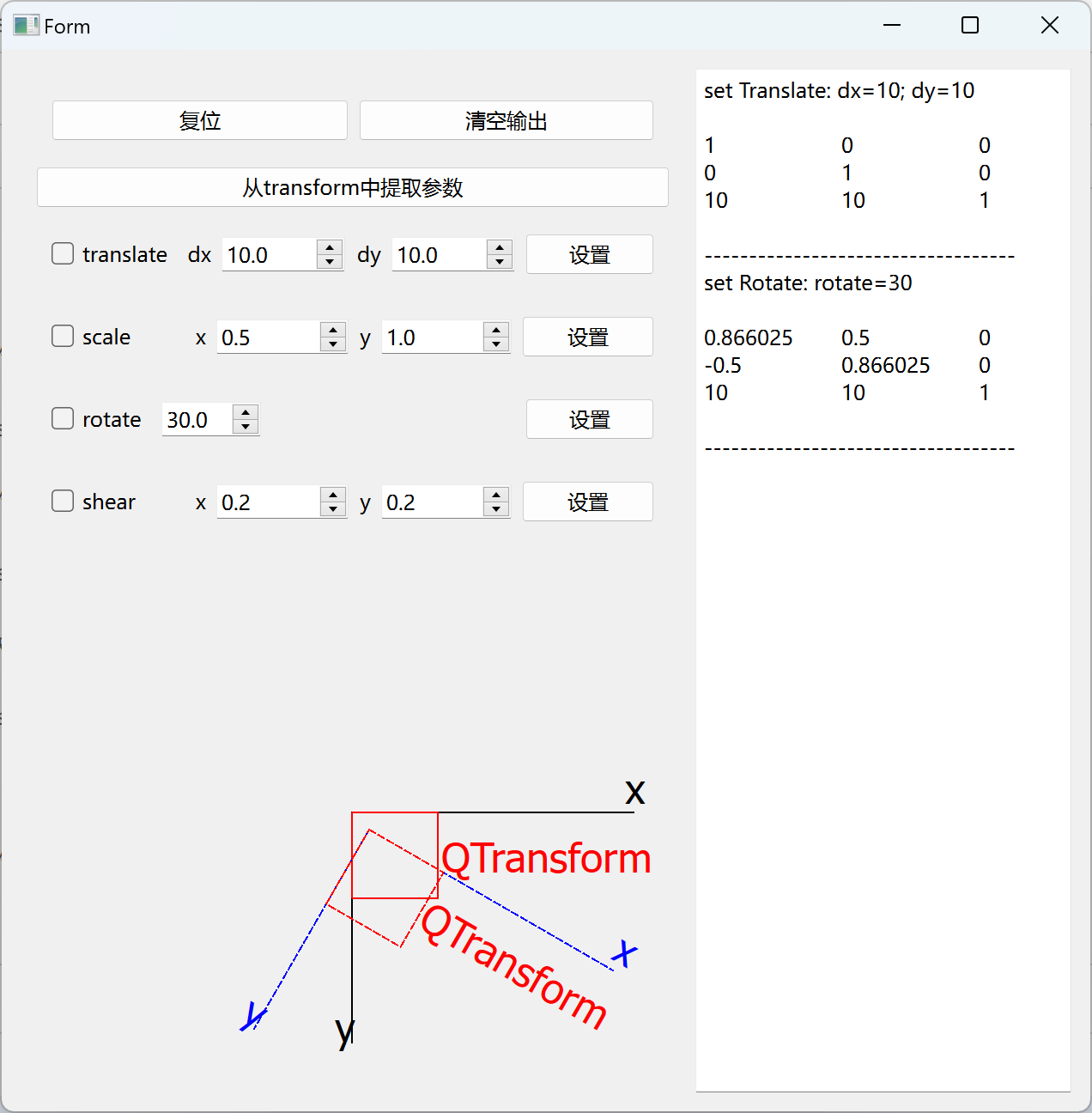
当按照 rotate -> translate 的顺序变换时,transform 矩阵中的dx dy的值受到 rotate 的影响不再是我们设置的值。
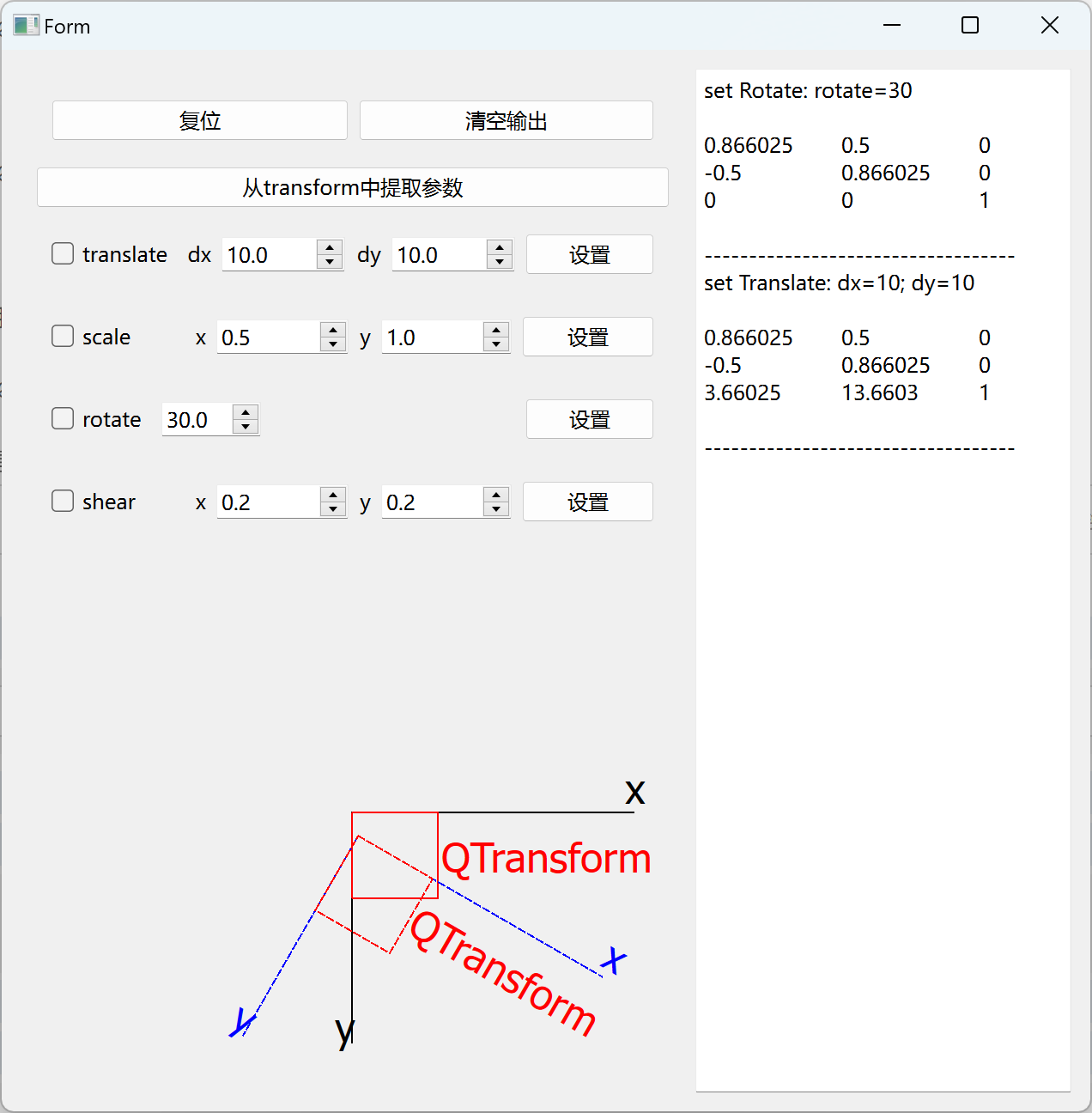
dx dy的计算如下图所示:
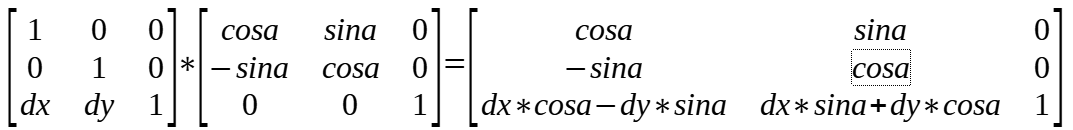
(3)scale 与 rotate
当按照 scale -> rotate的顺序变换时,transform 矩阵中的值的计算方式如下
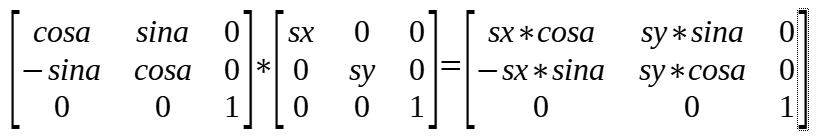
当按照 rotate -> scale 的顺序变换时,transform 矩阵中的值的计算方式如下

(4)shear 与 translate
当按照 translate -> shear 的顺序变换时,transform 矩阵中的值的计算方式如下
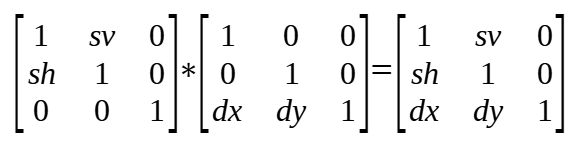
当按照 shear -> translate 的顺序变换时,transform 矩阵中的值的计算方式如下
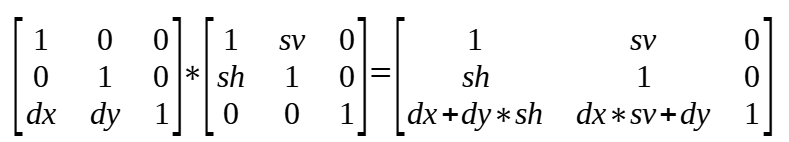
(5)shear 与 scale
当按照 scale -> shear 的顺序变换时,transform 矩阵中的值的计算方式如下
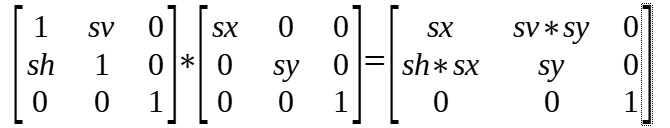
当按照 shear -> scale 的顺序变换时,transform 矩阵中的值的计算方式如下
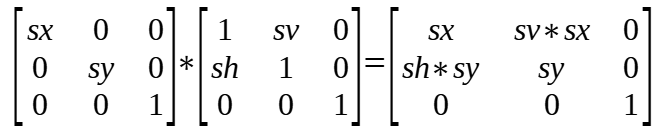
(6)translate scale rotate
按照 translate -> scale -> rotate 的顺序变换时,transform 矩阵中的值的计算方式如下
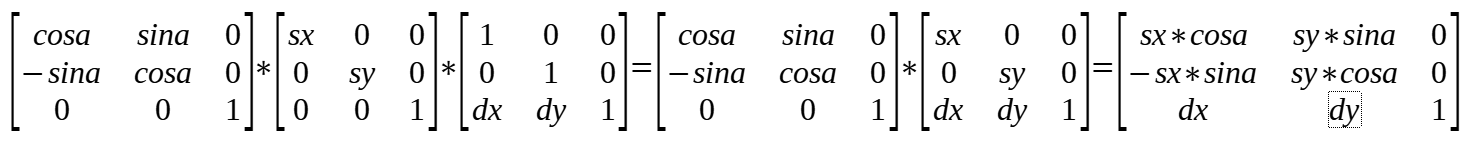
按照 translate -> rotate -> scale 的顺序变换时,transform 矩阵中的值的计算方式如下

按照 rotate -> translate -> scale 的顺序变换时,transform 矩阵中的值的计算方式如下
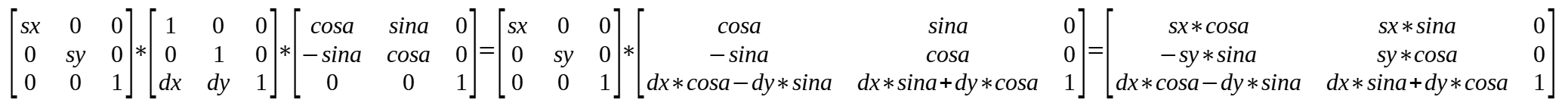
按照 rotate -> scale -> translate 的顺序变换时,transform 矩阵中的值的计算方式如下

按照 scale -> rotate -> translate 的顺序变换时,transform 矩阵中的值的计算方式如下
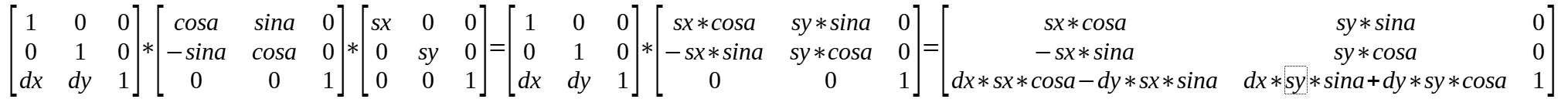
按照 scale -> translate -> rotate 的顺序变换时,transform 矩阵中的值的计算方式如下
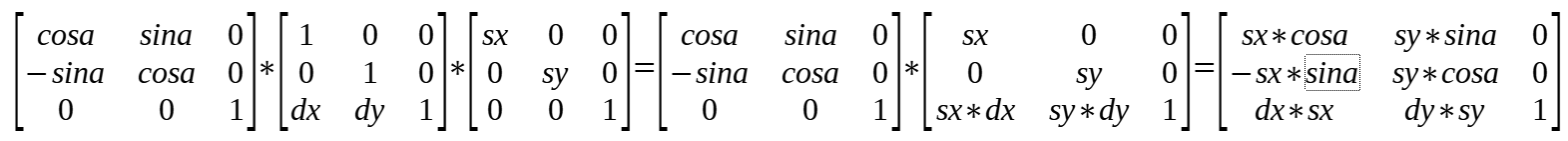
(7)shear translate scale rotate
按照 translate -> scale -> rotate -> shear 的顺序变换时,transform 矩阵中的值的计算方式如下
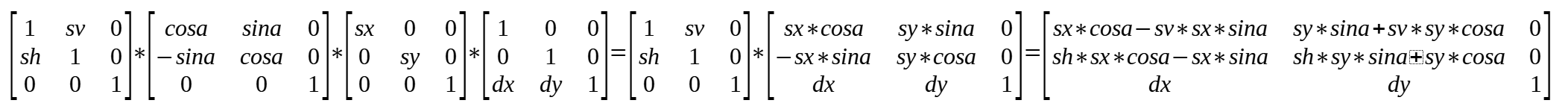
当 4 种变换混合在一起时,计算非常复杂,这里不再一一列举。可以看出当变换越多时,从transform 的矩阵中反推出原始值非常困难,如果使用过程中仅限于少数的变换,从上面的推导中是可以逆推出原始值的。另外,即使是同样的一组变换,执行顺序不同得到的结果也会不同,更直观的可以运行上面的程序仔细观察一下。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!