中国剩余定理分析及扩展

中国剩余定理（限制条件：模为两两互质）

中国剩余定理其实很早我们都接触过，在初中甚至小学的时候我们都有可能看到过这样的问题：有n个东西，三个人分剩两个，五个人分剩三个，七个人分剩两个，求n最少是多少。

求解这个问题古人就已经想到了很好的解决办法。

我们由题意易知：

x=2（mod）3；

x=3（mod）5；

x=2（mod）7；

如果x=n1+n2+n3。

n1是5,7的倍数，且n1%3=2。

n2是3,7的倍数，且n2%5=3。

n3是3,5的倍数，且n3%7=2。

故我们可以知道n1+n2+n3定是x的一个解。

那么怎么求n1，n2，n3呢？

我们由逆元知道。

（5*7）*inv（5*7,3）=1（mod）3；

（3*7）*inv(3*7,  5)  =  1（mod）5；

（3*5）*inv(3*5,  7)  =  1（mod）7；

故n1=2*5*7*inv（5*7,3），n2=3*3*7*inv(3*7,  5)，n3=2*3*5*inv(3*5,  7)  。

因为，中国剩余定理的模都是两两互质，必有逆元。用扩展欧几里得算法就可以求解，于是我们最后将求得的n1，n2，n3相加，最后的答案就是n=（n1+n2+n3）mod（lcm（3,5,7））。

 

扩展中国剩余定理：（求解模数不互质情况下的线性方程组）

注意：这种情况不一定有解。

 

这种情况就采用两两合并的思想，假设要合并如下两个方程：

　　那么得到：

　　我们需要求出一个最小的x使它满足：

　　那么x1和x2就要尽可能的小，于是我们用扩展欧几里得算法求出x1的最小正整数解，（判断是否方程组有解，就在于(a2-a1)%gcd(m1,m2)是否等于0，如果等于0有解，否则无解。）将它代回a1+m1x1，得到x的一个特解x′，当然也是最小正整数解。（为了防止特解大于lcm(m1,m2)。取模lcm(m1,m2)）

　　所以x的通解一定是x′加上lcm(m1,m2)∗k，这样才能保证x模m1和m2的余数是a1和a2。由此，我们把这个x′当做新的方程的余数，把lcm(m1,m2)当做新的方程的模数。（这一段是关键）

　　合并完成：

 

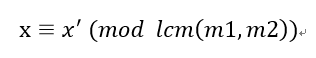
ps：个人觉得扩展中国剩余定理和中国剩余定理的区别在于

1、扩展可能无解，互质一定有解。

2、扩展用到了同余方程组合并的思想。而中国剩余定理只是单纯的求解逆元。虽然两者的求法都是用exgcd来求解，但是还是有区别点的。