LIS和LCS算法分析

LIS（最长上升子序列）

常规的解法就是动态规划。

mx[ j ]表示长度为j的上升子序列最小的值a[i];

dp[ i ]表示前i个数的最长上升子序列长度多少。

for(int i=1;i<n;i++)
 {
      int j;
      for( j=len;j>0;j--)
      {
           if(a[i]>mx[j])
           {
                 dp[i]=j+1;
                 mx[dp[i]]=min(mx[dp[i]],a[i]);//更新长度为j+1的最小值
                 break;
              }
       }
       if(j==0)//说明它是最小的
       {
             dp[i]=1;
             mx[dp[i]]=min(mx[dp[i]],a[i]);//更新
         }
 }

 

这就是解决LIS的核心代码，时间复杂度网上的博客说复杂度是O(n²) 说实话，个人感觉没有那么高的复杂度，比如HDU-5532就可以用这个方法解决，但是如果按n*n的复杂度来说是肯定要tle的，结果时间是982ms。看了一下，甚至比其他的更快了一些。。。

LIS在时间上的优化那就只能用n*logn的算法了

这个算法其实已经不是DP了，有点像贪心。至于复杂度降低其实是因为这个算法里面用到了二分搜索。本来有N个数要处理是O(n)，每次计算要查找N次还是O(n)，一共就是O(n^2)；现在搜索换成了O(logn)的二分搜索，总的复杂度就变为O(nlogn)了。

ps：最近还没用这个算法，感觉dp就挺好用的，等用了在更新吧，hhhhhh

 

LCS(最长公共子序列)

既然放在一起写，那么肯定有共同的地方，原理还是dp。

感觉还是由一个题目来看看到底怎么解决吧。

LCS裸题：HDU-1159

Input

abcfbc abfcab
programming contest 
abcd mnp

Output

4
2
0

Sample Input

abcfbc abfcab
programming contest 
abcd mnp

Sample Output

4
2
0

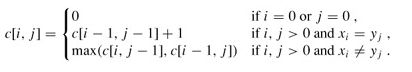
想一想是不是所有的情况都包括进去了

那么我们就可以在O(n*m)的复杂度解决这个问题了

#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
char a[1050],b[1050];
int dp[1050][1050];
int main()
{
    while(~scanf("%s %s",&a,&b))
    {
        memset(dp,0,sizeof(dp));
        int alen=strlen(a);
        int blen=strlen(b);
        for(int i=1;i<=alen;i++)
        {
            for(int j=1;j<=blen;j++)
            {
                if(a[i-1]==b[j-1])
                {
                    dp[i][j]=dp[i-1][j-1]+1;

                }
                else
                {
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        cout<<dp[alen][blen]<<endl;
    }
    return 0;
}