高斯朴素贝叶斯（Gaussian Naive Bayes）原理与实现——垃圾邮件识别实战

朴素贝叶斯（Naive Bayes）：

根据贝叶斯定理和朴素假设提出的朴素贝叶斯模型。

贝叶斯定理：

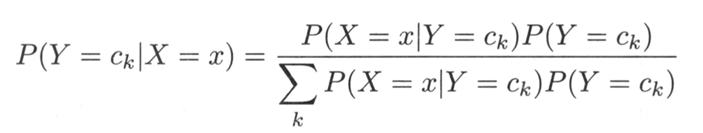
 朴素假设（特征条件独立性假设）：

代入可知朴素贝叶斯模型计算公式：

 

因为朴素贝叶斯是用来分类任务，因此：

 

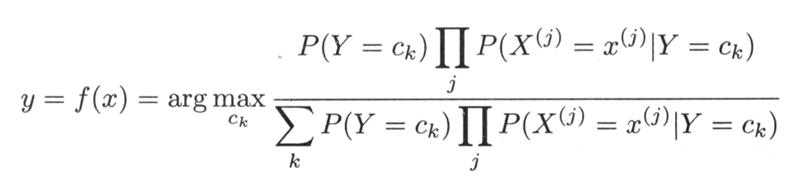
化简可知：

 

 

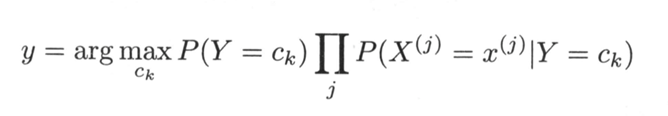
朴素贝叶斯模型除了上式所描述的以外，有三种常用的模型：

1、高斯朴素贝叶斯

2、多项式朴素贝叶斯

3、伯努利朴素贝叶斯

本篇主要是实现高斯朴素贝叶斯，因为它是最常用的一种模型。

高斯朴素贝叶斯：

适用于连续变量，其假定各个特征 𝑥_𝑖 在各个类别𝑦下是服从正态分布的，算法内部使用正态分布的概率密度函数来计算概率。

 

 𝜇_𝑦：在类别为𝑦的样本中，特征𝑥_𝑖的均值。

𝜎_𝑦：在类别为𝑦的样本中，特征𝑥_𝑖的标准差。

高斯朴素贝叶斯代码实现：

注释：

1、var_smoothing和epsilon的目的是防止一些特征的方差为0的情况（比如在垃圾邮件识别的时候，使用词袋模型很容易出现方差为0）

2、计算联合概率时并不使用连乘，对概率取自然对数，乘法变加法，降低计算复杂度，使模型更稳定。

import numpy as np
import collections
import math
class GaussianNB(object):
    def __init__(self):
        self.mp = {} #把y值映射到0-n之间的整数
        self.n_class = None #类别数
        self.class_prior= None #先验概率P(Y)
        self.means = None #均值
        self.vars = None  #方差
        self.var_smoothing =1e-9 #平滑因子
        self.epsilon = None #平滑值
    def _get_class_prior(self,y):
        cnt = collections.Counter(y)
        self.n_class = 0
        for k,v in cnt.items():
            self.mp[k] = self.n_class
            self.n_class+=1
        self.class_prior = np.array([ v/len(y) for k,v in cnt.items()])
        pass
    def _get_means(self,xx,y):
        new_y =np.array([self.mp[i] for i in y])
        self.means = np.array([ xx[new_y==id].mean(axis=0) for id in range(self.n_class)])
        # self.means shape: n_class * dims
        pass
    def _get_vars(self,xx,y):
        new_y = np.array([self.mp[i] for i in y])
        self.vars = np.array([xx[new_y == id].var(axis=0) for id in range(self.n_class)])
        # self.vars shape: n_class * dims
        pass
    def fit(self,X,Y):
        # X 必须是numpy的array; Y为list,对于X中每个样本的类别
        self._get_class_prior(Y)
        self._get_means(X,Y)
        self._get_vars(X,Y)
        self.epsilon = self.var_smoothing * self.vars.max() #选取特征中最大的方差作为平滑
        self.vars = self.vars + self.epsilon #给所有方差加上平滑的值
        pass
    def _get_gaussian(self,x,u,var):
        #计算在类别y下x的条件概率P(xj|y)的对数
        #return math.log(1 / math.sqrt(2 * math.pi * var) * math.exp(-(x - u) ** 2 / (2 * var)))
        return -(x - u) ** 2 / (2 * var) - math.log(math.sqrt(2 * math.pi * var))
    def predict(self,x):
        dims = len(x)
        likelihoods = []
        for id in range(self.n_class): #遍历每类yi，把每个特征的条件概率P(xj|yi)累加
            likelihoods.append(np.sum([self._get_gaussian(x[j], self.means[id][j], self.vars[id][j]) for j in range(dims)]))
        # 对先验概率取对数
        log_class_prior = np.log(self.class_prior)
        all_pros = log_class_prior + likelihoods
        #all_pros = self.standardization(all_pros)
        max_id = all_pros.argmax() #取概率最大的类别的下标
        for k,v in self.mp.items(): #转换为可读的y值
            if v== max_id:
                return k
        pass
    def standardization(self,x):
        mu = np.mean(x)
        sigma = np.std(x)
        return (x - mu) / sigma

# nb = GaussianNB()
# xx = np.array([[1,2,3],[11,12,1],[2,1,4],[15,16,1],[8,6,6],[19,13,0]])
# y = ['min','max','min','max','min','max']
# nb.fit(xx,y)
# print(nb.predict(np.array([0,0,0])))

垃圾邮件识别实战：

数据集：Trec06C数据集

 

笔者获取的数据集是处理过的

处理方式：随机选取：5000封垃圾邮件和5000封正常邮件；

预处理提取邮件正文，去掉换行符、多余空格等UTF-8文本格式，每封邮件正文在文件中保存为一行文本其中前5000 条为垃圾邮件，后5000 条为正常邮件。

 

特征提取：使用词袋模型进行特征提取（特征维度33453）

模型训练：模型训练和验证将数据集随机切分为训练集和测试集（40%）；使用GaussianNB高斯贝叶斯进行训练。

实验结果：在测试集上准确率达到了97.95%，效果还是不错的

 

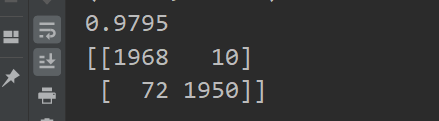
 实验代码：

注释：代码跑起来比较慢，主要是因为预测的函数并不是将所有的句子一起预测，而是一句一句预测了。最近没啥空改这个，等下次需要的时候再更新吧。

import numpy as np
import jieba
from sklearn.feature_extraction.text import CountVectorizer
from sklearn import model_selection, metrics
from GaussianNB import GaussianNB
file_path = 'email.txt'
file = open(file_path,encoding='utf-8')
data = file.readlines()
y = ['Spam']*5000+['Normal mail']*5000
split_data = []
for line in data:
    split_data.append(' '.join(jieba.lcut(line)))
print(split_data[-1])
#仅保留长度至少为2个汉字的词
cv = CountVectorizer(token_pattern=r"(?u)\b\w\w+\b")
xx = cv.fit_transform(split_data).toarray()
print(xx.shape)

x_train, x_test, y_train, y_test =  model_selection.train_test_split(xx,y,test_size=0.4)
gnb = GaussianNB()
gnb.fit(x_train,y_train)
y_pre  =[]
for x in x_test:
    y_pre.append(gnb.predict(x))
print(metrics.accuracy_score(y_test,y_pre))
print (metrics.confusion_matrix(y_test, y_pre))

 

参考资料：

1、《统计学习方法（第二版）》——李航

2、https://zhuanlan.zhihu.com/p/64498790