斜率优化DP学习笔记
终于打算开始学习斜优了...
首先先从一个简单的题目开始: P2365 任务安排
题目要求我们安排一些任务的完成,需要把他们进行分组完成,每组需要的费用为组内所有任务的费用系数和乘上最后一个任务完成的时间
除此之外,每组任务开始的时候都需要有一段准备时间
首先看看数据范围, \(n \leq 5000\) ,那么首先可以考虑 \(O(n^2)\) 的算法做
我们设 \(dp[i]\) 为前 \(i\) 个任务完成所需的最小费用,那么现在就会出现一个问题,我们不清楚前面 \(i\) 个任务分成了多少组
这个时候我们可以采用一种叫做费用提前的思想:
对于每次分组,准备需要的时间都是固定的,而每次都会使得后面所有任务完成时间推迟一个单位的准备时间,那么就会产生一个 \(s \times 剩余任务费用系数和\) 的费用
对此可以列出状态转移方程:
\(dp[i]=min (dp[j] + \sum_\limits{k=j+1}^{i}{f_k} \times \sum_\limits{k=1}^{i}{t_k} + s \times \sum_\limits{k=j+1}^{n}{f_k})\)
其中可以对 \(f_i\) 和 \(t_i\) 求前缀和来优化这个状态转移方程:
设 \(sum_i=f_i+sum_{i-1} T_i=t_i+T_{i-1}\)
那么有 \(dp[i]=min (dp[j] + (sum_i - sum_j) \times T_i + s \times (sum_n - sum_j))\)
时间复杂度为 \(O(n^2)\) ,可以通过.
代码如下:
#include <bits/stdc++.h>
using namespace std;
int dp[5001],n,s,t[5001],m[5001];
int main () {
memset (dp,0x3f,sizeof dp);
scanf ("%d %d",&n,&s);
for (int i=1,T,M;i<=n;++i) {
scanf ("%d %d",&T,&M);
t[i]=t[i-1]+T; //t[i]为时间的前缀和
m[i]=m[i-1]+M; //m[i]为价格系数的前缀和
}
dp[0]=0;
for (int i=1;i<=n;++i)
for (int j=0;j<i;++j)
dp[i]=min (dp[i],dp[j]+t[i]*(m[i]-m[j])+s*(m[n]-m[j])); //费用提前的状态转移方程
printf ("%d\n",dp[n]);
return 0;
}
但是接下来我们就考虑优化时间复杂度
我们需要求 \(dp[i]\) 的最小值,对此我们可以先将之前方程里的 \(min\) 函数去掉
再稍微整理变形:
\(dp[i]=dp[j] + (sum_i - sum_j) \times T_i + s \times (sum_n - sum_j)\)
\(\Rightarrow dp[i] - (sum_i - sum_j) \times T_i - s \times (sum_n - sum_j)=dp[j]\)
\(\Rightarrow dp[i] - sum_i \times T_i + sum_j \times T_i - s \times sum_n + s \times sum_j=dp[j]\)
\(\Rightarrow \mathop{\underline{dp[j]}}\limits_{y}=\mathop{\underline{( T_i + s )}}\limits_{k} \times \mathop{\underline{sum_j}}\limits_{x} + \mathop{\underline{dp[i] - sum_i \times T_i - s \times sum_n}}\limits_{b}\)
这样就得出了一个以 \(sum_j\) 为自变量, \(dp[j]\) 为因变量的一次函数
而求 \(dp[i]\) 的最小值,其实也就是求这个函数的截距 \(dp[i] - sum_i \times T_i - s \times sum_n\) 的最小值
又因为 \(j < i\) ,所以在求 \(dp[i]\) 的时候,函数内肯定是存在点的,同时函数的斜率 \(s + T_i\) 也是已知的,所以我们只需要将这个已知斜率的直线从下往上平移,当碰到第一个点时斜率肯定为当前的最小值
ok上图:
假设现在我们已经找到了这些点

然后我们用一条已知斜率的直线向上平移
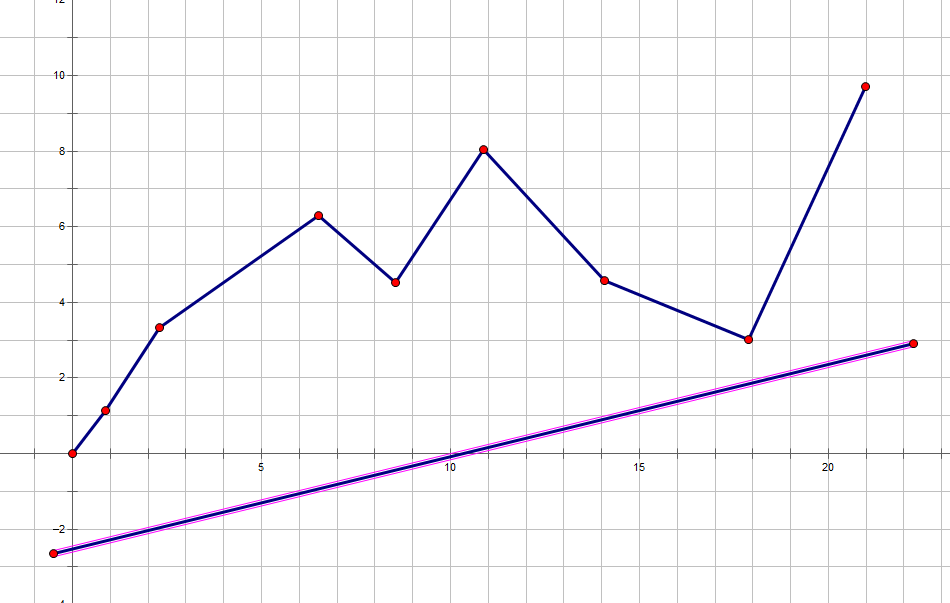
当触碰到第一个点的时候,目前直线的截距最小,也就可以算出当前的 \(dp[i]\) 的最小值
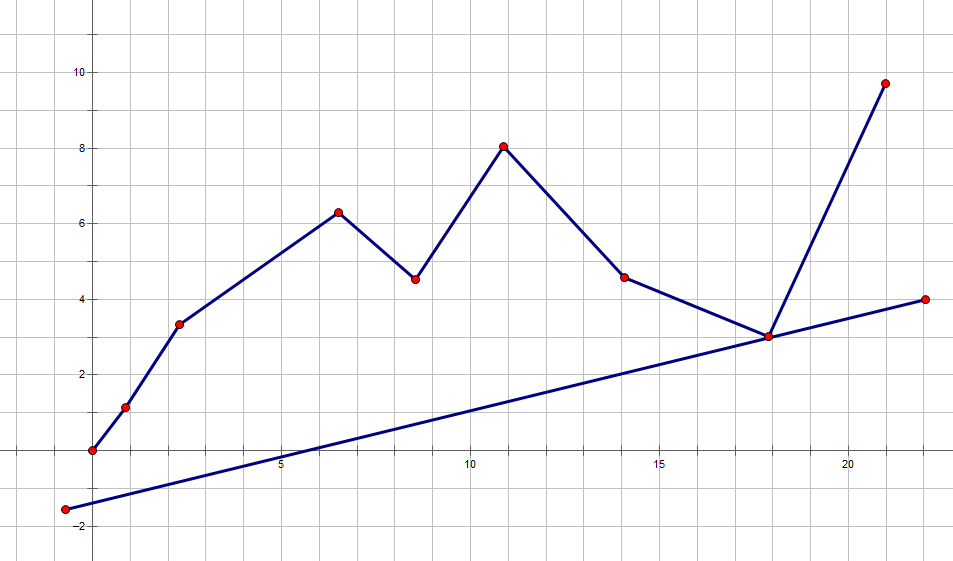
但是我们不可能每次都把所有点都列出来去寻找最小值
不过当一个点成为最优点的时候存在一个性质:它与它前一个点组成的线段的斜率比已知直线的斜率小,与它后一个点组成的线段的斜率比已知直线的斜率大:

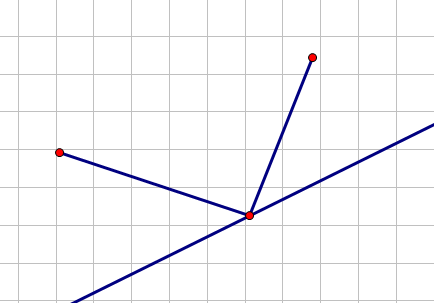
而一个不存在贡献的点当且仅当它与它前一个点组成的线段的斜率大于它与它后一个点组成线段的斜率:
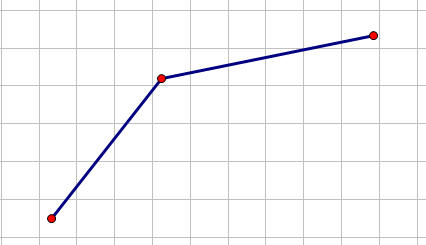
所以对于所有的点,我们可以用一个单调队列来维护,使队列内相邻两点的斜率单调递增
同时观察我们的斜率 \(s + T_i\) ,\(s\) 是不变的,而 \(T_i\) 是单调递增的,所以整个斜率都是单调递增的
所以直接从 \(1\) 遍历到 \(n\) ,同时维护队首,使队首与它下个点之间的斜率要大于当前对于 \(i\) 来说的斜率 \(s + T_i\)
虽然我也不知道我有没有说清,但是还是先上代码把:
#include <bits/stdc++.h>
using namespace std;
int dp[5001],n,s,t[5001],m[5001];
int que[20000],head,tail;
int main () {
memset (f,0x3f,sizeof f);
scanf ("%d %d",&n,&s);
for (int i=1,T,M;i<=n;++i) {
scanf ("%d %d",&T,&M);
t[i]=t[i-1]+T; //t[i]为时间的前缀和
m[i]=m[i-1]+M; //m[i]为价格系数的前缀和
}
dp[0]=0;
head=tail=1;
que[tail]=0;
for (int i=1;i<=n;++i) {
while (head<tail&&(dp[que[head+1]]-dp[que[head]])<=(t[i]+s)*(m[que[head+1]]-m[que[head]])) head++; //判断队首是否满足前两个点斜率大于当前函数的斜率、
//这里我采用的是用乘法来判断
dp[i]=dp[que[head]]-(t[i]+s)*m[que[head]]+t[i]*m[i]+s*m[n]; //计算dp[i]的最小值
while (head<tail&&(dp[que[tail]]-dp[que[tail-1]])*(m[i]-m[que[tail]])>=(dp[i]-dp[que[tail]])*(m[que[tail]]-m[que[tail-1]])) --tail; //判断加入当前元素后最后三个点是否满足斜率递增,如果不递增则弹出队尾元素
que[++tail]=i;
}
printf ("%d\n",dp[n]);
return 0;
}
每个元素只入队一次,时间复杂度 \(O(n)\)


