开始还以为就是简单的最短路,但是题目中有一个要求,可以使用sc使得某条路径的时间缩短一半,而且每张sc只能在一条路径中使用
那么对于每条路径就需要考虑是否使用sc来缩短时间,而且sc数量有限。
那么我们就可以使用一种叫做分层图的东西,将原本在二维上面的图上最短路拓展到多维,新增的维度就是我们分的层,每个层表示一种状态。
我们就先用 P4822 这一题来学习分层图吧..
题目的大致意思就是:
给定一张图,同时可以最多让k条不同的边的长度缩短一半
求节点1到节点n的最短路
然后题目给出的样例:
输入:
4 4 1
1 2 4
4 2 6
1 3 8
3 4 8
输出:
7
这里容易有个误区,就是先求出不使用sc的最短路,然后在这条最短路上的从大到小的路径依次使用sc来缩短路径
反例很容易找到:
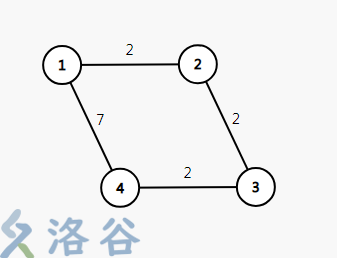
这里1-4的最短路径可以看出是 1-2-3 ,总代价为6,但是假设我们能使用一张sc,如果按上面的方法,总代价会变为 1+2+2=5 ,但是如果我们将这张sc用在1-4这条路上,总代价就变成了 7/2=3,是最优解,所以这种想法是错误的。
题目说有k张sc可以用,那么我们可以建k+1个图,也就是相当于把原图分层了k层(这里并非真正的复制,只是意思差不多是这样),第i张图表示我们使用了i张sc后的情况,i=0表示不使用任何sc,考虑用二维的dis数组dis[i][j]表示从1到i在第j层的最短路径。
假设我们要在图层P的路径K上使用sc,如果当前的图层不在最顶层,就可以将K的在P上的起点与K在P+1上的终点相连接,而代价为K的长度的1/2,这样就连接了两个图层,每次连接到新图层的代价都为原始代价的1/2,而无论在新图层还是原图层,所有路径的代价与最底层图一致
还是贴代码讲解吧:
#include <bits/stdc++.h>
using namespace std;
struct Map{
int next;
int to;
int w;
}node[10009]; // 链式前向星存图
int first[1009];
int book[1000][100]; // 标记
struct Heap{
int dis;
int sc;
int i;
}heap[40009]; // 建结构体存堆
int dis[1000][100];
// 存图上距离,其实dis[i][j]中的这个j也可以理解为使用了j张sc后1到i的距离
int Heap_size,cnt;
int ans=2147483647;
inline void Add_ (int u,int v,int w){ // 链式前向星存图
node[++cnt].next=first[u];
first[u]=cnt;
node[cnt].to=v;
node[cnt].w=w;
return;
}
inline void Puts_ (int DIS,int SC,int I){ // 用堆优化Dijkstra
heap[++Heap_size].dis=DIS;
heap[Heap_size].sc=SC;
heap[Heap_size].i=I;
int next,now=Heap_size;
while (now>1){
next=now>>1;
if (heap[now].dis>=heap[next].dis) return;
swap (heap[now],heap[next]);
now=next;
}
return;
}
inline Heap Gets_ (){
Heap res=heap[1];
heap[1]=heap[Heap_size--];
int next,now=1;
while ((now<<1)<=Heap_size){
int next=now<<1;
if (next<Heap_size&&heap[next+1].dis<heap[next].dis) next++;
if (heap[now].dis<=heap[next].dis) return res;
swap (heap[now],heap[next]);
now=next;
}
return res;
}
int n,m,k;
int main (){
scanf ("%d %d %d",&n,&m,&k); // 正常的输入 连边
for (register int i=1,u,v,w;i<=m;++i){
scanf ("%d %d %d",&u,&v,&w);
Add_ (u,v,w);
Add_ (v,u,w);
}
memset (dis,0x3f,sizeof (dis)); // dis数组初始化为极大值
dis[1][0]=0; // 第一层的起点的dis初始化为0
Puts_ (0,0,1); // 将起点放入堆中
while (Heap_size){
Heap Cirno=Gets_ (); // 取出堆顶
if (book[Cirno.i][Cirno.sc]) continue; // 如果该点已经用过了就跳过
book[Cirno.i][Cirno.sc]=1; // 标记该点已用
for (register int i=first[Cirno.i];i;i=node[i].next){
int to=node[i].to;
if (dis[to][Cirno.sc]>dis[Cirno.i][Cirno.sc]+node[i].w){ // 这里是在同一层上的Dij,和正常的差不多
dis[to][Cirno.sc]=dis[Cirno.i][Cirno.sc]+node[i].w;
Puts_ (dis[to][Cirno.sc],Cirno.sc,to); // 将更新后的点放入堆中
}
if ((Cirno.sc<k)&&(dis[to][Cirno.sc+1]>dis[Cirno.i][Cirno.sc]+node[i].w/2)){
// Cirno.sc<k 表示下一层非最顶层
// 即还可以继续向上使用sc拓展
// 注意更新的点在上一层
// 并且两点间距离要变为原来的1/2
dis[to][Cirno.sc+1]=dis[Cirno.i][Cirno.sc]+node[i].w/2;
Puts_ (dis[to][Cirno.sc+1],Cirno.sc+1,to); // 放入堆的操作也差不多,注意Cirno.sc要+1表示是上一层的dis
}
}
}
for (int i=0;i<=k;++i) // 最后再扫一遍得出最小值,因为无法保证使用所有的sc一定距离最小
ans=min (ans,dis[n][i]);
printf ("%d\n",ans);
return 0;
}
这里主要还是要理解所谓的将图分层的意思,分层图这种思路多用于那些能用一定次数将某些边的长度增大或者减小来求最短路的题目
当然也可以用DP做
最后的最后再放几道luogu上的可以用分层图做的题目吧:



