传统声学模型之HMM和GMM

声学模型是指给定声学符号(音素)的情况下对音频特征建立的模型。

数学表达

用 \(X\) 表示音频特征向量 (观察向量)，用 \(S\) 表示音素 (隐藏/内部状态)，声学模型表示为 \(P(X|S)\)。

但我们的机器是个牙牙学语的孩子，并不知道哪个音素具体的发出的声音是怎么样的。我们只能通过大量的数据去教他，比如说在拼音「é」的时候对应「鹅」的发音，而这个过程就是 GMM 所做的，根据数据建立起「é」这个拼音对应的音频特征分布，即 \(P(x|s=é)\)。孩子学会每个拼音的发音后，就可以根据拼音拼读一个单词 / 一个句子，但你发现他在读某段句子的时候，听起来好像怪怪的，你检查发现是他把某个拼音读错了，导致这句话听起来和常理不符。而这个怪怪的程度就是你听到这个音频特征序列的时感觉这个音频序列以及其背后的拼音出现的可能性的倒数，这部分则是通过 HMM 来建模的。

总结一下，GMM 用于对音素所对应的音频特征分布进行建模，HMM 则用于音素转移和音素对应输出音频特征之间关系的建模。

HMM

即为隐马尔可夫模型（Hidden Markov model，HMM）

HMM 脱胎于马尔可夫链，马尔可夫链表示的是一个系统中，从一个状态转移到另一个状态的所有可能性。但因为在实际应用过程中，并不是所有状态都是可观察的，不过我们可以通过可观察到的状态与隐藏状态之间的可能性。因此就有了隐马尔可夫模型。

HMM 要遵循的假设：

• 一阶马尔可夫假设：下一个状态只依赖于当前的状态。因此多阶马尔可夫链可简化为

  \[P(s_{t+1} | s_1,s_2,\ldots,s_t) = P(s_{t+1} | s_t) \]

• 输出无关假设：每个输出只取决于当前 (内部/隐藏) 状态，和前一个或多个输出无关。

声学模型为什么要用HMM？

因为声学模型建立的是在给定音素序列下输出特定音频特征序列的似然 \(P(X|S)\)，但在实际情况中，我们只知道音频特征序列，并不知道其对应的音素序列，所以我们需要通过 HMM 建立音频特征与背后的每个音素的对应关系，以及这个音素序列是怎么由各个音素组成的。

上两个假设可以引申出 HMM 中主要的两种概率构成：

• 从一个内部状态 \(i\) 转移到另一个内部状态 \(j\) 的概率称为转移(Transition) 概率，表示为 \(a_{ij}\)。
• 在给定一个内部状态 \(j\) 的情况下观察到某个观察值 \(x_t\) 的概率称为输出(Emission)概率，表示为 \(b_j(x_t)\)。

HMM 的三个经典问题

• 评估问题 Estimation
• 解码问题 Decoding
• 训练问题 Learning

⚠️：后文提到的状态即指的是内部 / 隐藏状态。

评估问题

评估问题就是说，我已知模型参数 \(\theta\) (输出概率以及转移概率)，最后得到的观察序列为某个特定序列 \(X\) 的概率是多少。

在刚才的例子中，就是孩子已经知道每个拼音后面可能接什么拼音，每个拼音怎么读，当他读出了某段声音，这段声音的概率是多少。

因为在观察序列固定的情况下，有多种可能的状态序列 \(S\)，而评估问题就是要计算出在所有可能的状态下得到观察序列的概率，表示为

\[\begin{aligned} P(X) = \sum_S P(X | S) P(S) \\ \end{aligned} \]

在当前的公式里，我们暂时先忽略固定的参数 \(\theta\)。根据一阶马尔可夫假设，时刻 \(t\) 的状态都只取决于时刻 t-1 的状态，因此单个状态序列出现的概率表示为

\[\begin{aligned} P(S) &= P(s_1) \prod^T_{t=2} P(s_t|s_{t-1}) \\ &= \pi_k \prod^T_{t=2} a_{ij} \end{aligned} \]

其中， \(\pi_k\) 表示时刻1下状态为 \(k\) 的概率。

根据输出无关假设，在时刻 \(t\) 观察序列的值只取决于时刻 \(t\) 的状态，因此观察序列关于状态序列的似然表示为

\[P(X|S) = \prod_{t=1}^T P(x_t|s_t) = \prod_{t=1}^T b_j(x_t) \]

因此整个观察序列出现的概率为

\[\begin{aligned} P(X) &= \sum_S P(X | S) P(S) \\ &= \sum_S \pi_k b_k(x_1) \prod^T_{t=2} a_{ij} b_j(x_t) \end{aligned} \]

由于 \(i,j,k\) 都表示可能的状态，假设有 \(n\) 种状态，那么计算该概率的事件复杂度就为 \(O(n^T)\)，可谓是指数级别了。

因此，前人开动了脑筋，提出了在该问题上将时间复杂度将为多项式时间的方法。

似然前向算法

该方法采用了分治 / 动态规划的思想，在时刻 \(t\) 下的结果可以利用时刻 \(t-1\) 的结果来计算。

在时刻 \(t\)，观察序列的概率表示为前 \(t\) 个时刻的观察序列与时刻 \(t\) 所有可能的状态同时出现的概率和

\[P(x_1,x_2,\ldots,x_t) = \sum_{j\in N} P(x_1,x_2,\ldots,x_t,s_t=j) \]

其中， \(N\) 表示所有可能的状态的集合。

而连加符号的后面部分被定义为前向概率 \(\alpha_t(j)\)，而它可以被上一个时刻的前向概率迭代表示。

\[\begin{aligned} \alpha_t(j) &=P(x_1,x_2,\ldots,x_t,s_t=j) \\ &= \sum_{i\in N} P(x_1,x_2,\ldots,x_{t-1},s_{t-1}=i)P(s_t|s_{t-1}=i)P(x_t|s_{t}=j) \\ &= \sum_{i\in N}\alpha_{t-1}(i) a_{ij} b_j(x_t) \end{aligned} \]

通过该方法，当前时刻下某个状态的概率只需要遍历上一时刻所有状态的概率 (\(n\))，然后当前时刻的所有状态的概率和也只需要遍历当前的所有状态就可以计算得到 (\(n\))，考虑到观察序列持续了 \(T\) 个时刻，因此时间复杂度降为 \(O(n^2T)\)。

整个过程总结如下

1. 初始化：根据初始的状态分布，计算得到时刻1下每个状态的前向概率 \(\alpha_1(k) = \pi_k b_k(x_1)\)
2. 对于每个时刻，计算该时刻下每个状态的前向概率 \(\alpha_t(j) = \sum_{i\in N}\alpha_{t-1}(i) a_{ij} b_j(x_t)\)
3. 最终得到结果 \(P(X) = \sum_{i\in N}\alpha_{T}(i)\)

解码问题

解码问题就是说在得到 HMM 模型之后，我们如何通过观察序列找到最有可能的状态序列。在语音识别中，在给定的音频片段下，找到对应的各个音素。

还是刚才的例子，我们需要猜测孩子读出的这段声音最有可能对应什么样的拼音序列，这就是解码问题。

Viterbi 算法

数学表示

给定在时间 \(t\) 下的内部状态为 \(j\)，局部最优概率 \(v_t(j)\) 表示的是在时刻 \(t\) 观察序列与最优内部状态序列的联合概率。

\[v_{t}(j)=\max _{s_{0}, s_{1} \ldots s_{t-1}} P\left(s_{0}, s_{1}, \ldots, s_{t-1}, x_{1}, x_{2}, \ldots, x_{t}, s_{t}=j | \theta\right) \]

同样也可以根据时间递归表示为

\[v_{t}(j)=\max_{i \in N} v_{t-1}(i) a_{i j} b_{j}\left(x_{t}\right) \]

算法具体流程如下

1. 初始化：根据初始的状态分布，计算得到时刻1下每个状态的最优概率 \(v_1(k) = \pi_k b_k(x_1)\)
2. 对于每个时刻，计算该时刻下每个状态的局部最优概率 \(v_t(j) = \max_{i\in N}v_{t-1}(i) a_{ij} b_j(x_t)\)，记录下最优局部最优序列 \((s_1^*,s_2^*,\ldots,s_{t-2}^*) \bigcup (s_{t-1}^*)\)
3. 最终得到全局最优概率 \(P(X,S^*) = \max_{i\in N} v_T(i)\)
4. 得到全局最优序列 \(S^* = \arg \max_{i\in N} v_T(i), S^* = (s_1^*,s_2^*,\ldots,s_T^*)\)

在表示上很类似于上面的前向算法，只是加和变成了取最大值。具体推导流程也就不再赘述了。两者的区别可以看下图(来源) ，红线表示解码路径，黑线表示评估路径。

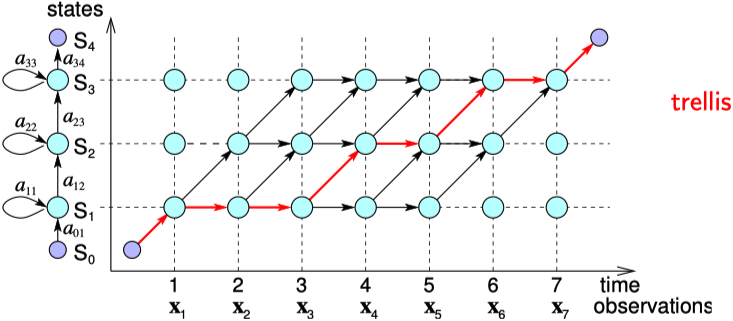
不过这张图是简化的状态，即状态序列 \(S\) 是确定的情况下的状态转移与观察序列之间的关系。

🤔思考：为何每次取局部最优最后就能得到全局最优？

这和一阶马尔可夫假设有关，因为每一个时刻的状态只取决于上一个时刻的状态，因此只要上一个时刻每一个状态的前向概率是最大的，再乘上这一时刻对某个状态的转移概率和输出概率，而这两个概率在参数表里是固定的，因此再选出乘出来的概率最大即可保证该时刻在这个时刻为这个状态的概率最大，直到最后一个时刻。（类似于动态规划的状态转移方程思想）

训练问题

训练 (learning) 问题主要是如何学习 HMM 模型参数(输出概率和表现概率)的问题。在语音识别中，即在一开始只有音频和标注的情况下，如何学习到模型。

还是刚刚那个例子，假如说你没有教孩子，但给了他本语文教材和对应的录音磁带，他需要通过教材中的拼音和磁带中的录音来训练语感 (比如说哪个拼音读什么音，每个拼音之后可能会跟什么拼音)。他自学成才了以后我们才能做刚刚那两个问题。

所以说训练问题是评估和解码问题的基础，但是是三个问题中最复杂的，因为它是无闭式解的。

HMM 参数估计方法：

• 最大似然 ：Baum-Welch 算法
• 贝叶斯：最大后验
• 判别训练：MMI，MCE，MPE，sMBR

Baum–Welch 算法

HMM训练问题的标准算法，又称前向后向算法，是 EM 算法的特例。

后向算法的表示和前向算法类似，而后向概率 \(\beta_t(i)\) 表示的是在给定 \(t\) 时刻状态为 \(i\)，看到时刻 t+1 到时刻 \(T\) 观察序列的概率，表示为

\[\begin{aligned} \beta_{t}(i) &= P(x_{t+1},x_{t+2},\ldots,x_{T}|s_{t} = i) \\ &= \sum_{j \in N} P(s_{t+1}=j | s_{t}=i) P(x_{t+1} | s_{t+1}=j) P(x_{t+1},x_{t+2},\ldots,x_{T}|s_{t+1} = j) \\ &= \sum_{j \in N} a_{ij}b_{t+1}(j)\beta_{t+1}(j) \\ \beta_{T}(i) &= 1 \\ \end{aligned} \]

最后，整个观察序列出现的概率用后向算法表示为

\[P(X) = \sum_{j \in N} \pi_{j} b_{j}\left(x_{1}\right) \beta_{1}(j) \]

为了能学习 HMM 模型参数，我们可以通过一个最大似然估计的变体评估我们的转移概率 \(\hat{a}_{ij}\) ，可以表示为

\[\hat{a}_{ij} = \frac{从状态i转移到状态j的期望次数}{从状态i转移到所有状态的期望次数} \]

但如何计算这些次数是个问题，假设我们可以估计在时刻 \(t\) 和给定观察序列下从状态 \(i\) 转移到状态 \(j\) 的概率，那我们就可以把每个时刻的概率加起来作为从状态 \(i\) 转移到状态 \(j\) 的总次数。

我们定义了一个「状态转移占有(occupation)率」 \(\xi_{t}(i,j)\) ，作为给定所有观察序列的情况下在时刻 \(t\) 状态为 \(i\) 后下一时刻转移到状态 \(j\) 的概率，表示为

\[\begin{aligned} \xi_{t}(i,j) &=P\left(s_{t}=i, s_{t+1}=j | X, \theta\right) \\ &=\frac{P\left(s_{t}=i, s_{t+1}=j, X | \theta\right)}{P(X | \theta)} \end{aligned} \]

下图(修改自来源)直观地展示了 \(\xi_{t}(i,j)\) 分子部分的计算过程，因此其分子可以表示为 \(\alpha_{t}(i) a_{i j} \beta_{t+1}(j) b_{j}\left(x_{t+1}\right)\)

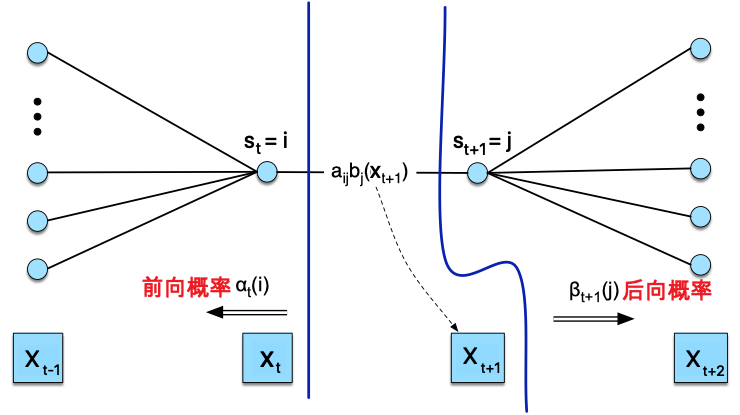
而其分母部分则可以表示为某个时刻所有状态的前向概率和后向概率的乘积和

\[\begin{aligned} P(X | \theta) &= \sum_{k \in N}P(X_{1}^t, s_t=k | \theta)P(X_{t+1}^T | s_t = k, \theta)\\ & = \sum_{k\in N} \alpha_{t}(k) \beta_{t}(k)\\ \end{aligned} \]

因此 \(\xi_{t}(i,j)\) 最后可表达为

\[\xi_{t}(i,j)=\frac{\alpha_{t}(i) a_{i j} \beta_{t+1}(j) b_{j}\left(x_{t+1}\right)}{\sum_{k\in N} \alpha_{t}(k) \beta_{t+1}(k)} \]

我们可以把各个时刻的 \(\xi_{t}(i,j)\) 加起来作为「从状态 \(i\) 转移到状态 \(j\) 的期望次数」，再将状态 \(j\) 所有可能的状态下的期望次数加和就可以得到「从状态 \(i\) 转移到所有状态的期望次数」，从而计算得到 \(\hat{a}_{ij}\)。

\[\hat{a}_{i j}=\frac{\sum_{t=1}^{T-1} \xi_{t}(i,j)}{\sum_{t=1}^{T-1} \sum_{j \in N}\xi_{t}(i,j)} \]

我们同样需要一个用于计算输出概率 \(\hat{b}_j(v_k)\) 的最大似然估计公式，\(v_k\) 表示的是输出序列中的第 \(k\) 个音素对应的音频特征。

\[\hat{b}_j(x_t) = \frac{在状态j下观察到v_k的期望次数}{在状态j下所有的期望观察次数} \]

为了计算这个公式，我们需要知道在给定观察序列的情况下在时刻 \(t\) 的状态为 \(i\) 的概率，我们将其称为「状态占有率」 \(\gamma_{t}(i)\),

\[\begin{aligned} \gamma_{t}(i) &=P\left(s_{t}=i | X, \theta\right)\\ &= \frac{P\left(s_{t}=i, X | \theta\right)}{P(X | \theta)} \\ \end{aligned} \]

而分子部分的概率其实刚刚我们在计算 \(\xi_{t}(i,j)\) 分母时已经用到了，即时刻 \(t\) 下为状态 \(i\) 的前向概率乘上后向概率。

\[\begin{aligned} \gamma_{t}(i) &= \frac{P(X_{1}^t, s_t=i | \theta)P(X_{t+1}^T | s_t = i, \theta)}{p(X | \theta)}\\ &=\frac{\alpha_{t}(i) \beta_{t}(i)}{\sum_{k\in N} \alpha_{t}(k) \beta_{t}(k)} \end{aligned} \]

得到了 \(\gamma_{t}(i)\) 以后，就可以用他来计算 \(\hat{b}_j(v_k)\) 了，我们加上了所有 \(x_t\) 为 \(v_k\) 的 时刻的 \(\gamma_{t}(i)\) 作为分子，而分母就是所有时刻的 \(\gamma_{t}(i)\) 之和。

\[\hat{b}_{i}\left(v_k\right)=\frac{\sum_{t=1,s.t. x_t=v_k}^{T} \gamma_{t}(i)}{\sum_{t=1}^{T} \gamma_{t}(i)} \]

同时，\(\hat{a}_{ij}\) 的分母也可以用 \(\gamma_{t}(i)\) 来表示

\[\hat{a}_{i j}=\frac{\sum_{t=1}^{T-1} \xi_{t}(i,j)}{\sum_{t=1}^{T-1} \gamma_{t}(i)} \]

得到新的 HMM 参数 \(\theta_1\) 后，又可以计算得到新的 \(\theta_2\)，同样又可以估计得到新的最佳 \(\theta_1\)，一直迭代这个过程直到收敛。

在 E 步建立 \(P(\gamma,\xi | x, a, b)\)，然后 M 步 找到将上式最大化的参数 \(a, b\)，具体流程如下

1. 初始化：初始化转移概率矩阵 \(A\)，以及输出概率矩阵 \(B\)
2. E 步：
   1. 计算得到每个时刻的每个状态的前向概率 \(\alpha_t(i)\) 和后向概率 \(\beta_t(i)\)
   2. 更新状态占有率 \(\gamma_{t}(i)\) 和 状态转移占有率 $$\xi_{t}(i,j)$$
3. M 步：
   1. 计算得到期望概率：
      1. 期望初始化概率 \(\hat{\pi}_{i}=\gamma_{1}(i)\)
      2. 期望转移概率 \(\hat{a}_{ij}\)
      3. 期望输出概率 \(\hat{b}_j(v_k)\)
4. 不停迭代 E 步 M 步 直到收敛

尽管从原理上来讲前向后退算法可以完全无监督地学习参数，但实际上初始化非常重要。 因此，通常会给算法额外的信息。 例如，对于基于 HMM 的语音识别，通常手动设定 HMM 结构，并且从一组观察序列 \(X\) 中仅训练输出概率和(非零的)转移概率。

GMM

高斯混合模型 (Gaussian mixture model，GMM) 就是用混合的高斯随机变量的分布来拟合训练数据（音频特征）形成的模型。该方法提供了一种基于规则的方法来衡量一个音素和被观察音频帧的「距离」。

给定一个音素，我们可以使用 GMM 学习观察值的特征向量，这个概率分布允许我们在给定一个音素(状态)下计算音频段的似然 \(P(x | s)\).

单变量高斯分布

假设观察向量中某个特征 \(x\) 的分布为正态分布，那么该特征 \(x\) 的似然函数可以表示为均值为 \(\mu\) 方差为 \(\sigma^2\) 的高斯分布

\[f(x|\mu,\sigma)=\mathcal{N}\left(\mu, \sigma^{2}\right)=\frac{1}{\sigma \sqrt{2 \pi} } e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} \]

在被标记了状态的训练数据下，我们可以计算的到关于状态 \(i\) 的均值和方差

\[\begin{array}{l} \mu_{i}=\frac{1}{T} \sum_{t=1}^{T} x_{t} & \text { s.t. } x_{t} \text { is state } i \\ \sigma_{i}^{2}=\frac{1}{T} \sum_{t=1}^{T}\left(x_{t}-\mu_{i}\right)^{2} & \text{ s.t. } q_{t} \text { is state } i \end{array} \]

高斯分布易于从训练数据中学习并且让我们有了一个良好的似然函数 \(f(x|\mu,\sigma)\)。在语音识别中我们可以为每个音素(状态)学到一个高斯分布，这将作为似然概率，也可以作为 HMM 中的输出概率。

根据 HMM 在时刻 \(t\) 下所处状态 \(i\) 的概率，将每个观察向量 \(x_t\) 按比例分配给每个可能的状态 \(i\)。而在时刻 \(t\) 处于状态 \(i\) 的概率在 HMM 中为表示为状态占有率 \(\gamma_t(i)\)，因此可以在将高斯分布的参数期望表示为

\[\bar{\mu}_{i}=\frac{\sum_{t=1}^{T} \gamma_{t}(i) x_{t}}{\sum_{t=1}^{T} \gamma_{t}(i)} \quad \bar{\sigma}_{i}^{2}=\frac{\sum_{t=1}^{T} \gamma_{t}(i)\left(x_{t}-\mu_{i}\right)^{2}}{\sum_{t=1}^{T} \gamma_{t}(i)} \]

多变量高斯分布

在多变量高斯分布中，我们将均值 \(\mu\) 替换为多个特征均值的向量 \(\boldsymbol{\mu} = \left(\mu_1,\ldots,\mu_n\right)^T\)，将方差 \(\sigma\) 替换为协方差矩阵 \(\Sigma\in\mathbb{R}^{n\times n}\)，其中第 \(i\) 行 \(j\) 列个元素表示为 \(\sigma_{ij}^2 = E\left[(x_i-\mu_i)(x_j-\mu_j)\right]\)，最终的高斯分布表示为

\[f(x | \boldsymbol{\mu}, \Sigma)=\frac{1}{(2 \pi)^{n / 2}|\Sigma|^{1 / 2}} e^{-\frac{1}{2}(x-\boldsymbol{\mu})^{T} \Sigma^{-1}(x-\boldsymbol{\mu})} \]

通过快速傅立叶变化 FFT 得到的特征之间是相关的，但通过梅尔倒谱相关系数 MFCC 得到的特征之间是不相关的。在特征不相关的情况下，协方差矩阵是对角阵，计算和存储代价小了很多。这样我们就可以单独考虑每个声学特征的方差。

混合高斯分布

但单个高斯分布可能并不能很好地来对特征的分布进行建模 (现实世界总是没有那么理想化)，因此采用多个加权的高斯分布来对对特征分布建模。

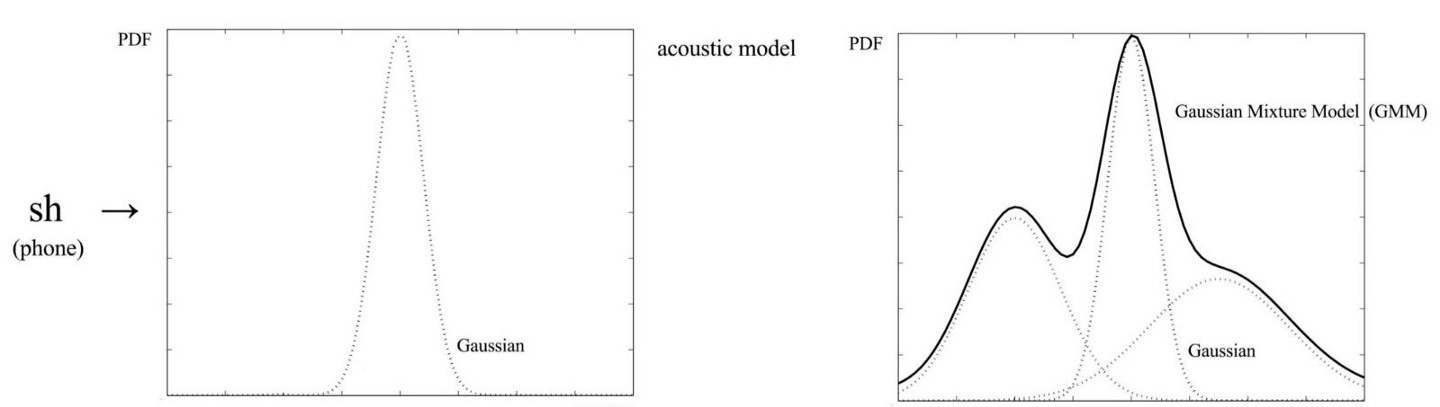
比如说上图(来源)中的3分量 GMM，有6个高斯参数加上3个权重。

因此，对于一个 HMM 的状态 \(j\)，观察特征向量 \(x\) 的似然函数可以表示为

\[b_{j}(x)=p(x | s=j)=\sum_{m=1}^{M} c_{j m} \mathcal{N}\left(x ; \boldsymbol{\mu}_{j m}, \Sigma_{j m}\right) \]

其中 M 为 GMM 的分量数，而 \(c_{j m}\) 表示的是在状态 \(j\) 下第 \(m\) 个分量的权重。

在实际的 GMM 训练中，通常采用 EM 算法来进行迭代优化，以求取 GMM 中的加权系数及各个高斯函数的均值与方差等参数。

缺点：

• 不能考虑语音的顺序信息
• 高斯混合分布也很难拟合非线性或者近似非线性的数据特征

最后再重声一下，GMM 用于对音素所对应的音频特征分布进行建模，而 HMM 则用于音素转移和音素对应输出音频特征之间关系的建模。

写不动了，HMM 和 GMM 梳理推导了好久，如果各位读者有不懂的欢迎留言讨论～👏

参考链接：

• Speech Recognition — GMM, HMM
• 【PDF】CHAPTER A Hidden Markov Models
• 【PPT】CS 224S-Lecture 5: GMM Acoustic Modeling and Feature Extraction
• 【PPT】声学模型-V2-赵老师