算法改进 | java语言中判断素数
参考文章:http://blog.csdn.net/kp_liu/article/details/37569507
http://blog.csdn.net/huang_miao_xin/article/details/51331710
https://www.zybang.com/question/93c4703c84c5ad3c1c34b1e6672b0568.html
素 数
——只能被1和它本身整除的数(除1以外,1既不是素数也不是合数)
-
-
-
-
-
-
- 现给出一个数N(N为正整数),编写方法判断其是否为素数。
-
-
-
-
-
直观想法
遍历从2至N-1,看是否存在N的约数。若存在,即不是素数。
基础改进
不必从2遍历至N-1,数N若是合数,则其至少可由两个因数相乘得到,这两个数必定一个大于(或等于)sqrt(n),一个小于(或等于)sqrt(n),因此仅需遍历至sqrt(n)即可。
改进方法一 (偶数;缩小判断范围;)
Step 1 (除2以外)判断N是否为偶数,若是,则判断结束——不是素数;
Step 2 若N不是偶数但是合数,它的因数绝不可能是偶数(原因 偶数×偶数=偶数;偶数×奇数=偶数),
因此判断奇数N的因数时,可以省去对偶数的判断。(i+=2)
1 static boolean isPrime_1(int N){ 2 int tmp=(int)Math.sqrt(N); 3 //Step 1 4 if(N==2)return true; 5 if(N%2==0)return false; 6 //Step 2 7 for(int i=3;i<tmp;i+=2) 8 if(N%i==0)return false; 9 10 return true; 11 }
改进方法二 (质数分布规律;pruning策略;)
一个关于质数分布的规律:大于等于5的质数一定和6的倍数相邻(即大于等于5的质数x,都可以表示为x=6k+1 或者是 x=6k-1,k为>0的自然数)。
但要注意:在6的倍数相邻两侧并不是一定就是质数。
证明
直观看,大于等于5的自然数都可以用6k-1,6k,6k+1,6k+2,6k+3,6k+4,6k+5的形式表示,显然6k+2 = 2(3k+2),6k+3 = 3(2k+1),6k+4 = 2(3k+2)都是合数,再除去6k本身,因此大于等于5的质数都可以表示成6k+1和6k+5(当x大于等于6时,6k+5与6k-1可表示同一个数)的形式。
数学证明
- 质数x大于等于5,则一定不是3的倍数,也不是2的倍数。
- 如果一个自然数不是3的倍数,有两种情况,设 x=3p+1或x=3p+2 (p>1)
- 如果一个自然数不是2的倍数,有一种情况,设 x=2t+1 (t>3)
1)若x=3p+1,且x=2t+1
则x=3p+1=2t+1 >> x-1=3p=2t
>> 3p=2t,可知p为2的倍数,t为3的倍数,
设p=2k,>> t=3k
因此x=2*3k+1=6k+1
2)若x=3p+2,且x=2t+1
则x=3p+2=2t+1
>> 3p+1=2t,因此3p为奇数,即p为奇数,设p=2k-1
则3*(2k-1)+1=2t,>> t=3k-1
因此x=2(3k-1)+1=6k-1
Step 1 单独判断2、3,都是素数;
Step 2 判断N是否在6的倍数的两侧,若不在,则判断结束——不是素数;
Step 3 数N在6的倍数两侧也不一定是质数,还需判断是否能在6的倍数两侧的数中找到数N的因数,若找不到,才可判定为质数。
(为什么只需在“6的倍数两侧的数”中寻找因数?
原因 所有合数可由质数的积组成,所以N只需要与可能是质数(即6的倍数的前后两个数)的数进行取余)
1 static boolean isPrime_2(int N){ 2 int tmp=(int)Math.sqrt(N); 3 //Step 1 4 if(N==2||N==3)return true; 5 //Step 2 6 if(N%6!=1&&N%6!=5)return false; 7 //Step 3 8 for(int i=5;i<=tmp;i+=6) 9 if(N%i==0||N%(i+2)==0)return false; 10 /*此处 11 * i表示形式为6k+5的数, 12 * i+2表示形式为6k+1的数 13 */ 14 15 return true; 16 }
方法比较 && 代码测试
测试代码
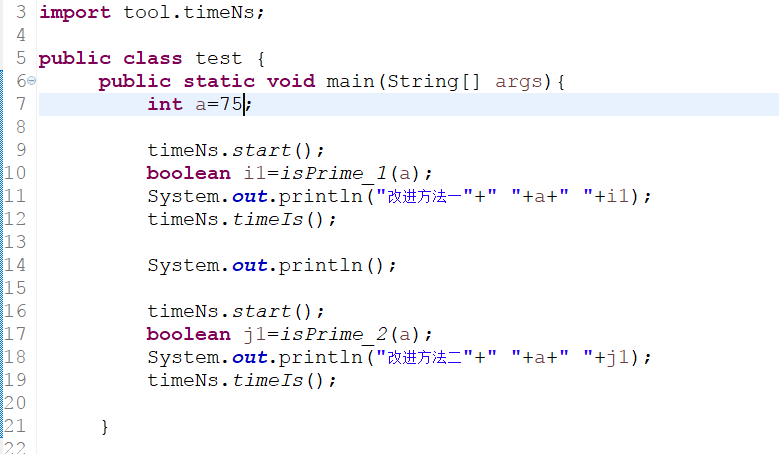
数据情况






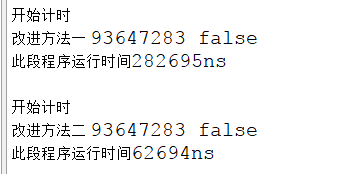
-
-
-
-
-
-
- “改进方法二” 完胜
-
-
-
-
-
E N D



