之前做拓扑图,本来打算整一套坐标系统在里面的,后来因为时间原因暂时用了最原始的方法实现。现在稍稍得闲,重新开始思考这个问题。不过在搜索的时候,意外发现.Net Framework类库中自带的有实现坐标系转换功能的类。Reflector了一把,发现代码看不懂了——都是利用矩阵操作的。矩阵这玩意儿,几年没用早忘完了。于是认真学习了一把,顺便把如何用矩阵进行坐标转换的过程记录和注解一下。文中部分内容摘取自MSDN,搜索“变换的矩阵表示形式”即可找到。
首先review一下矩阵的基础知识:
m×n 矩阵是排列在 m 行和 n 列中的一系列数。下图显示几个矩阵。

可以通过将单个元素相加来加合两个尺寸相同的矩阵。下图显示了两个矩阵相加的示例。
m×n 矩阵可与一个 n×p 矩阵相乘,结果为一个 m×p 矩阵。第一个矩阵的列数必须与第二个矩阵的行数相同。例如,一个 4×2 矩阵与一个 2×3 矩阵相乘,产生一个 4×3 矩阵。
矩阵的行列的平面点可视为矢量。例如,(2, 5) 是具有两个组件的矢量,(3, 7, 1) 是具有三个组件的矢量。两个矢量的点积定义如下:
(a, b) • (c, d) = ac + bd
(a, b, c) • (d, e, f) = ad + be + cf
例如,(2, 3) 和 (5, 4) 的点积是 (2)(5) + (3)(4) = 22。(2, 5, 1) 和 (4, 3, 1) 的点积是 (2)(4) + (5)(3) + (1)(1) = 24。请注意,两个矢量的点积是数字,而不是另一个矢量。另外请注意,只有当两个矢量的组件数相同时,才能计算点积。
将 A(i, j) 作为矩阵 A 中第 i 行、第 j 列的项。例如,A(3, 2)是矩阵 A 中第 3 行、第 2 列的项。假定 A、B 和 C 是矩阵,且 AB = C,则 C 的项计算如下:
C(i, j) =(A 的第 i 行)•(B 的第 j 列)
下图显示了矩阵相乘的几个示例。
以第二个等式为例,假设等式两边的矩阵分别是a、b、c,1*3的矩阵和3*2的矩阵相乘,得到的结果为1*2的矩阵。其中c[0][0] = a[0][0]*b[0][0]+a[0][1]*b[1][0]+a[0][2]*b[2][0],c[0][1]=a[0][0]*b[0][1]+a[0][1]*b[1][1]+a[0][2]*b[2][1]。
矩阵的加法、乘法,可以用来做坐标转换。我们通常使用3*3(如果不需要旋转,则2*2的矩阵即可)的矩阵来做平面上的各种坐标转换,包括x/y轴的平移、旋转。现在来看一个简单的坐标系转换的例子:假设我们的客户区分辨率是100*100,要在客户区中心点画一个点,这个点的坐标是(x, y)。现在如果我们调整了客户区分辨率为400*300,此时如果还需要保持这个点的相对位置不变,计算他的坐标应该是(x * 400 / 100, y * 300 / 100)。这个计算过程很简单,那么用矩阵操作应该如何来实现呢?
我们将这个点视为一个1*2的矩阵,将其乘以一个2*2的矩阵,得出的仍然是一个1*2的矩阵,就是新的坐标了。由于屏幕分辨率在x、y轴分别扩大为原来的4倍和3倍,那么我们只要将点的x、y轴坐标都扩大到原来的4、3倍即可。公式如下:
![]()
等式左边的第二个矩阵,就是用来实现坐标转换的矩阵。其中b[0][0]就是x轴的扩大倍数,b[1][1]就是在y轴上的扩大倍数。这里面b[0][1]和b[1][0]永远是0。坐标系的这种转换,叫做线性变换。
OK。看完这个例子,是不是觉得用矩阵比直接计算还麻烦?嗯,对于这种简单的情况是这样的。不过别急,继续看坐标系旋转的情况,如果现在要求这个客户区逆时针旋转30度,要保持这个点的相对位置不变,他的新坐标应该是多少呢?
普通的计算的公式就不陈述了,这就是个初中几何题目。我们直接来看怎样通过矩阵操作实现。首先看公式:在二维空间中,旋转可以用一个单一的角 θ 定义。作为约定,正角表示逆时针旋转。关于原点逆时针旋转 θ 的矩阵是:

也就是说,逆时针旋转30度的新坐标就是:
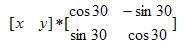
当然,除此之外,坐标系还有平移,但是这个就简单了,只是一个简单的矩阵加法。比如(x, y)向右平移一个单位,用矩阵就是[x, y] + [1, 0]就是是(x + 1, y)。
下图显示了应用于点 (2, 1) 的几个变换:
前图中显示的所有变换都是线性变换。某些其他变换(如平移)不是线性的,不能表示为与 2×2 矩阵相乘的形式。假定您要从点 (2, 1) 开始,将其旋转 90 度,在 x 方向将其平移 3 个单位,在 y 方向将其平移 4 个单位。可通过先使用矩阵乘法再使用矩阵加法来完成此操作。
后面跟一平移(与 1×2 矩阵相加)的线性变换(与 2×2 矩阵相乘)称为仿射变换,如上图所示。放射变换(先乘后加)可以通过乘以一个3*3的矩阵来实现,若要使其起作用,平面上的点必须存储于具有虚拟第三坐标的 1×3 矩阵中。通常的方法是使所有的第三坐标等于 1。例如,矩阵 [2 1 1] 代表点 (2, 1)。下图演示了表示为与单个 3×3 矩阵相乘的仿射变换(旋转 90 度;在 x 方向上平移 3 个单位,在 y 方向上平移 4 个单位):

在前面的示例中,点 (2, 1) 映射到了点 (2, 6)。请注意,3×3 矩阵的第三列包含数字 0,0,1。对于仿射变换的 3×3 矩阵而言,情况将总是如此。重要的数字是列 1 和列 2 中的 6 个数字。矩阵左上角的 2×2 部分表示变换的线性部分,第 3 行中的前两项表示平移。

在使用3*3的矩阵做仿射变换时候,表示点的矩阵变成了一个1*3矩阵,这个矩阵中的最后一个值(a[0][2])必须设置成1。对于3*3矩阵b,其最后一列的值是多少是没有关系的,因为他们不会影响结果中的前两列。不过如上,经常将他们设置为0,0,1。这一列对于坐标转换的结果并没有任何影响,但是他们是必须的,因为矩阵相乘必须满足开篇所讲的“相乘的两个矩阵第一个矩阵的列数必须与第二个矩阵的行数相同”。
在.Net Framework中,又一个矩阵类“Matrix”。其内置了点坐标转换(TransformPoints)、平移(Translate)、缩放(Scale)、旋转(Rotate)方法。下面的示例创建了复合变换(先旋转 30 度,再在 y 方向上缩放 2 倍,然后在 x 方向平移 5 个单位)的矩阵:
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);
除了Matrix类以外,.Net Framework中也有其他用于坐标系转换的类,比如System.Drawing.Graphics。具体用法请查阅相关文档。
以上只是利用矩阵进行平面坐标系转换的方法。如果是三位坐标系,也是可以利用矩阵来操作的,但Matrix类不行,因为其本身的定位就是“封装表示几何变换的 3 x 3 仿射矩阵”。
不过,可以附上几个三维空间的旋转公式:

上面是分别绕单个轴旋转的公式。复杂的旋转可以通过这三个公式组合而成,任何 3 维旋转矩阵都可以用这三个角 θx, θy, 和 θz 来刻画,并且可以表示为 roll, pitch 和 yaw 矩阵的乘积。


