[18/11/28]二叉树的生成(以二叉搜索树为例)

1、思想

          这里构建的二叉树是一棵二叉搜索(排序)树(BST)，由于二叉排序树的中序遍历是有序的，便于观察。

  (1)、首先定义节点和树的数据类型

             typedef struct node{  //定义节点的数据类型

                               int data;

                               struct node* left;

                              struct node* right;

             } Node;

            typedef struct { // 定义树的数据类型

                             Node* root; 

           } Tree;

(2)、插入和生成

          在二叉排序树中插入一个新元素，要保证插入后仍然满足BST性质。插入过程是：若二叉排序树Tree为空，则创建一个关键字为data的node节点，作为它的根节点；否则将data与根节点比较，若data<根节点，则插在左子树上，否则插在右子树上.

【代码示例】

//1、二叉树的生成(以二叉搜索(排序)树为例，中序遍历是有序的)

#include <stdio.h>
#include <stdlib.h>


typedef struct node{  //定义节点的数据类型
    int data;
    struct node* left;
    struct node* right;
} Node;

typedef struct { // 定义树的数据类型
    Node* root;
} Tree;
void inorder(Node* node){ //中序遍历(二叉搜索树的中序序列是有序的)：左 根 右
    if(node!=NULL){
        inorder(node->left);
        printf("%-4d",node->data); //node 是节点，调用data用node->data 而非 node.data
        inorder(node->right);
    }
}
                                    // | 递归模型 f(node)=0;
int get_height(Node* node){ //求高度   |          f(node)=MAX{f(node->left),f(node->right)}+1
    if(node==NULL){                  //|
            return 0;
    }else{
        int left_height=get_height(node ->left);
        int right_height=get_height(node ->right);
        return (left_height > right_height)?(left_height+1):(right_height+1);//返回左右子树最大的那个，然后加1(根节点那层)
    }
}

int get_max(Node* node){ //求普通二叉树的最大值 假设全是正数 (二叉搜索树的更简单，就在最右边)
    if(node==NULL){
            return -1; //若节点为空，返回-1
    }else{
        int left_max=get_max(node->left);//分别获取左右子树的最大值
        int right_max=get_max(node->right);
        int max=node->data; //获取根节点的值

        int temp =(left_max>right_max)?left_max:right_max; //进行比较，返回3个数中最大的那个
        return (temp>max)?temp:max;
    }

}

void insert(Tree* tree,int value){ //构建二叉树
    Node* node= malloc(sizeof(Node)); //node 是个指针

    node -> data  = value; //初始时根的左右子树全为空
    node -> left  = NULL;
    node -> right = NULL;

    if(tree->root == NULL){
        tree->root=node;  //如果根节点为空（这个数是第一个数），则插入这个数
    }else{
        Node* temp=tree->root; //temp:临时节点，即当前所比较的节点
        while(temp!=NULL){
                if(value < temp->data){ //如果比根节点小 ，插在左子树上
                        if(temp->left==NULL){
                                temp->left=node;
                                return;
                        }else{
                            temp=temp->left;
                        }
                }else{ //如果比根节点大，插入在右子树上
                    if(temp->right==NULL){
                                temp->right=node;
                                return;
                        }else{
                            temp=temp->right;
                    }
                }
        }
    }
}

int main()
{
    int arr[9]={3,7,8,2,5,11,9,1,6};
    Tree tree;
    tree.root=NULL;
    for(int i=0;i<9;i++){
            insert(&tree,arr[i]);//依次插入各个节点
    }
    inorder(tree.root); //中序输出
    printf( "\nh=%-4d",get_height(tree.root) ); //输出高度
    printf( "\nmax=%-4d",get_max(tree.root) ); //输出最大值


    return 0;
}

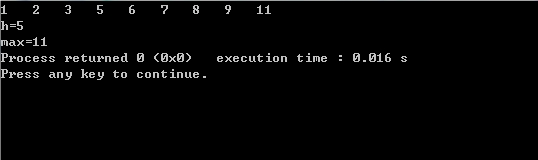
【结果示例】