每日一题 - 剑指 Offer 48. 最长不含重复字符的子字符串
题目信息
-
时间: 2019-07-02
-
题目链接:Leetcode
-
tag: 动态规划 哈希表
-
难易程度:中等
-
题目描述:
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
示例1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
注意
1. s.length <= 40000
解题思路
本题难点
长度为 N 的字符串共有 (1+N)N/2 个子字符串(复杂度为 O(N^2 ) ),判断长度为 N 的字符串是否有重复字符的复杂度为 O(N) ,使用暴力法解决的复杂度为 O(N^3) 。
具体思路
考虑使用动态规划降低时间复杂度。
- 状态定义:设动态规划列表 dp ,dp[j] 代表以字符 s[j 为结尾的 “最长不重复子字符串” 的长度。
- 转移方程:固定右边界 j ,设字符 s[j] 左边距离最近的相同字符为 s[i] ,即 s[i]=s[j] 。
- 当 i<0时,即 s[j] 左边无相同字符,则 dp[j]=dp[j−1]+1 ;
- 当 dp[j−1] < j−i 时,说明字符 s[i] 在子字符串 dp[j−1] 区间之外 ,则 dp[j]=dp[j−1]+1 ;
- 当 dp[j−1] > j−i 时,说明字符 s[i] 在子字符串 dp[j−1] 区间之中 ,则 dp[j] 的左边界由 s[i] 决定,即 dp[j]=j−i ;
注意:当 i<0 时,由于 dp[j−1]≤j 恒成立,因而 dp[j−1]<j−i 恒成立,因此分支 1. 和 2. 可被合并。
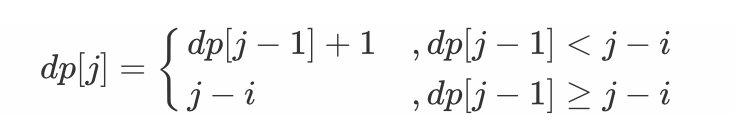
代码
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> dic = new HashMap<>();
int res = 0, tmp = 0;
for(int j = 0; j < s.length(); j++) {
int i = dic.getOrDefault(s.charAt(j), -1); // 获取索引 i
dic.put(s.charAt(j), j); // 更新哈希表
tmp = tmp < j - i ? tmp + 1 : j - i; // dp[j - 1] -> dp[j]
res = Math.max(res, tmp); // max(dp[j - 1], dp[j])
}
return res;
}
}
复杂度分析:
- 时间复杂度 O(N) :其中 N为字符串长度,动态规划需遍历计算 dp列表。
- 空间复杂度 O(1) : 字符的 ASCII 码范围为 0 ~ 127 ,哈希表 dic 最多使用 O(128)=O(1) 大小的额外空间。
其他优秀解答
解题思路
双指针 + 哈希表
哈希表 dic统计: 指针 j遍历字符 s,哈希表统计字符 s[j]最后一次出现的索引 。
更新左指针 i : 根据上轮左指针 i 和 dic[s[j]] ,每轮更新左边界 i ,保证区间 [i+1,j] 内无重复字符且最大
更新结果 res : 取上轮 res 和本轮双指针区间 [i+1,j] 的宽度(即 j−i )中的最大值。
代码
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character,Integer> dic = new HashMap<>();
int i = -1,res = 0;
//遍历字符串 s
for(int j = 0; j < s.length();j++){
//遍历到 s[j] 时,可通过访问哈希表 dic[s[j]] 获取最近的相同字符的索引 i
if(dic.containsKey(s.charAt(j))){
//取最大值因为防止abba的情况出现
i = Math.max(i,dic.get(s.charAt(j)));
}
//使用哈希表统计 各字符最后一次出现的索引位置
dic.put(s.charAt(j),j);
res = Math.max(res,j-i);
}
return res;
}
}


