遗传算法
1、遗传算法的概念
遗传算法是借鉴生物进化过程而提出的一种算法,这是一种随机化算法,是建立在不确定性基础上的。算法模拟了种群一代一代进化的过程:通过评估函数进行优胜劣汰的选择,通过交叉和变异来模拟生物的进化。优胜劣汰是遗传算法的核心,根据优胜劣汰的策略的不同,算法最终的效果也是不同的。遗传算法将实际问题的解定义为进化对象的个体,对若干个体组成的种群进行选择、交叉(杂交)和变异处理,就这样每次对种群进行一次这样的处理,种群就视为进化了一代,循环往复,只要选择的评估和选择策略合适,若干次进化后种群中就会出现优秀的个体(即问题的近似最优解)。需要注意的是,遗传算法并不是一个具体的算法,它只是一种思想,针对不同的问题,遗传算法的设计都是各不相同的。
2、遗传算法的原理
遗传算法依据是物竞天择,适者生存,说到进化论,就先复习一下初中的生物学知识。基因指的是一个单独的遗传因子,包含一组不能再拆分的生物学特征,而染色体指的是一组基因的组合;接下来是种群和个体,生物的进化以群体的形式进行,该群体就叫做种群,种群中的每个生物就是个体,种群内部的个体之间是相互联系相互影响的,最终影响着整个种群的进化;遗传指的是下一代个体会遗传继承上一代个体的部分基因,这使得个体的生物学特征能遗传到下一代,但是遗传是不稳定的,会有一定的概率发生基因突变,基因突变产生的新的生物学特征可能会提高个体的环境适应能力,也可能反之。
在遗传算法中,生物繁殖就是基因交叉算法的过程,将种群中的个体进行两两部分基因编码片段的互换,得到下一代个体。遗传算法中的基因突变算法是通过直接替换掉个体基因中的某几个基因编码实现的(或者其他方式)。在编写遗传算法时,往往都需要定义两个变量,来控制基因交叉和基因突变发生的概率,最终使得算法收敛到近似最优解。选择也是遗传算法中很重要的一部分,选择就是根据个体的适应度,按照一定规则从上一代种群中选择一些优秀的个体遗传到下一代种群中,适应度指的是个体对环境的适应程度,适应度差的个体会被淘汰,最终适应度高的个体会越来越多,遗传算法一般会根据实际情况选择一个适应度评估函数,来评估种群中个体的适应度。
3、遗传算法基本框架
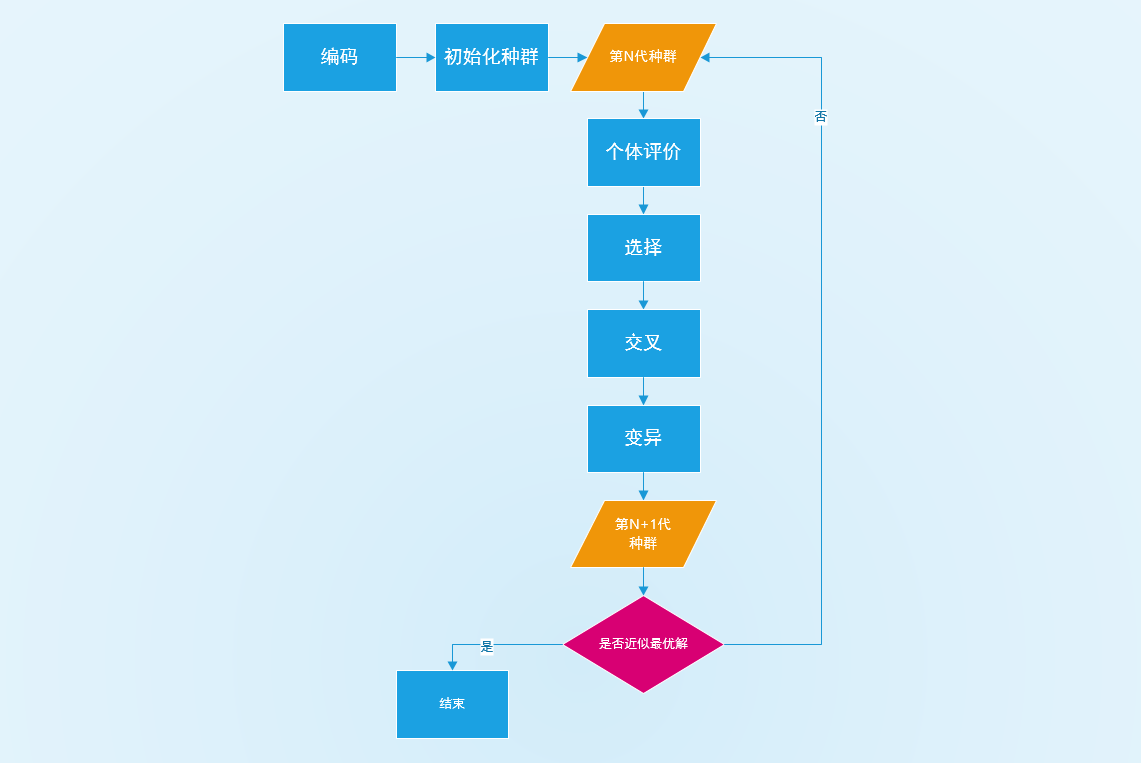
先从编码说起,编码是设计遗传算法的首要步骤,遗传算法不能直接处理问题空间的参数,必须把它们转换成遗传空间的由基因按一定结构组成的染色体或个体。这一转换操作就叫做编码,也可以称作问题的表示。评估编码策略常采用以下3个规范:完备性(问题空间中的所有解在遗传算法中都有编码值与之对应)、健全性(遗传算法中每个编码值在问题空间都有对应的值)、非冗余性(遗传算法中的每个编码值与问题空间中的解一一对应)。目前的几种常用的编码技术有二进制编码,浮点数编码,字符编码等等。
适应度评估函数:进化论中的适应度,是表示某一个体对环境的适应能力,也表示该个体繁殖后代的能力。适应度评估函数是用来判断群体中的个体的优劣程度的指标,它是根据所求问题的目标函数来进行评估的。遗传算法在搜索进化过程中一般不需要其他外部信息,仅用评估函数来评估个体或解的优劣,并作为以后遗传操作的依据。适应度函数的值一般要取正值,将目标函数映射成求最大值形式且函数值非负的适应度函数是必要的。适应度函数的设计主要满足以下条件:单值、连续、非负、最大化; 合理、一致性;计算量小;通用性强。在具体应用中,适应度函数的设计要结合求解问题本身的要求而定。适应度函数设计直接影响到遗传算法的性能。
初始群体选取:遗传算法中初始群体中的个体是随机产生的。一般来讲,初始群体的设定可采取如下的策略:第一种是根据问题固有知识,设法把握最优解所占空间在整个问题空间中的分布范围,然后,在此分布范围内设定初始群体。第二种是先随机生成一定数目的个体,然后从中挑出最好的个体加到初始群体中,这种过程不断迭代,直到初始群体中个体数达到了预先确定的规模。
4、遗传算法运算过程
选择、交叉、变异是遗传算法的三个遗传算子。选择算子又称复制算子,是遗传算法中保证优良基因传播的基本方式,对应的是”适者生存“的群体进化现象。交叉算子对应的是物种交配和繁殖产生的基因交换现象。变异算子对应的是基因突变这种现象。其中交叉和变异算子用于产生新个体。
选择:指的是从群体中选择优胜的个体,淘汰劣质个体的操作,又称为再生算子(也有些资料上称为复制算子)。选择的目的是把优化的个体(或解)直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的,目前常用的选择算子有这几种:适应度比例方法、随机遍历抽样法、局部选择法。个体被选后,可随机地组成交配对,以供后面的交叉操作。
交叉:遗传算法中起核心作用的是遗传操作的交叉算子。所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作。通过交叉,遗传算法的搜索能力得以飞跃提高。交叉算子根据交叉率将种群中的两个个体随机地交换某些基因,能够产生新的基因组合,期望将有益基因组合在一起。根据编码表示方法的不同,可以有以下的算法:实值重组、离散重组、中间重组、线性重组、扩展线性重组、二进制交叉、单点交叉、多点交叉、均匀交叉、洗牌交叉、缩小代理交叉。
变异:对群体中的个体串的某些基因座上的基因值作变动。依据个体编码表示方法的不同,可以有实值变异和二进制变异。一般来说,变异算子操作的基本步骤如下:对群中所有个体以事先设定的变异概率判断是否进行变异;对进行变异的个体随机选择变异位进行变异。遗传算法引入变异的目的有两个:一是使遗传算法具有局部的随机搜索能力。当遗传算法通过交叉算子已接近最优解邻域时,利用变异算子的这种局部随机搜索能力可以加速向最优解收敛。显然,此种情况下的变异概率应取较小值,否则接近最优解的积木块会因变异而遭到破坏。二是使遗传算法可维持群体多样性,以防止出现未成熟收敛现象。此时收敛概率应取较大值。
5、遗传算法的运行参数
除了三个遗传算子和适应度函数,还有这四个参数会影响算法的最终效果,分别是种群大小、交叉概率、变异概率、进化代数。种群大小M表示种群中个体的数量,种群大小决定了遗传算法的多样性,M值越大,多样性越好,但会加大计算量;交叉概率P1决定了产生新个体的频率,P1太小的话会导致新个体产生速度慢,影响种群多样性,太大的话会使基因遗传不稳定。变异概率P2也是影响种群多样性的参数之一,变异概率应该取一个较小的值才符合遗传学原理。进化代数T是遗传算法的退出条件,如果T太小,会使得还没进化成熟就退出了,如果T太大,当种群进化已经接近最优解时,后面的进化所产生的变化已经很小了,这样会影响算法运行效率,一般T最小进化100代。
6、遗传算法在游戏开发中的应用
在游戏开发中,遗传算法只是一种寻找问题的最佳解决方案的方法。当问题的因素有某些不可预测性时,遗传算法会很适合,可以让游戏AI适应设计师没办法预测的情况。游戏设计时,最不可预测的因素是玩家的操作,游戏设计师必须去预测玩家的行为,从而让游戏更加智能、有挑战性,实际上又很难预测出每个玩家的行为。遗传算法牵涉到试误法,你可以让游戏世界有多种可能的解法,然后找出表现最好的解法,当然,解法并非对每位玩家都是一成不变的,这正是遗传算法的优势所在,让游戏AI去适应各个玩家,只要遗传算法设计合理,它的灵活性远胜于传统的if else条件判断。
7、最后
这两天学了一下遗传算法,这篇文章也只是遗传算法一些的理论知识,过几天再写一篇游戏开发中使用遗传算法的示例~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号