【NOIP模拟赛】制胡窜 题解

今天浅试了一下vscode的typora插件和cnblog插件，这篇文章是typora插件编写，cnblog插件发布的

Problem

题目描述

给你两个字符串 \(S\) 和 \(T\) ，有 \(q\) 次询问，每次询问给定一个 \(k\) 。

对于每次询问，你需要输出至少多少个 \(S\) 拼起来才能不为 \(k\) 个 \(T\) 拼起来的子序列。

注意是子序列！！！ 吐槽：考试的时候因为看成子串了所以浪费了半天。

输入格式

第一行一个整数 \(q\)。

第二行 \(S\)

第三行 \(T\)

接下来 \(q\) 行，每行一个正整数 \(k\) 。

输出格式

\(q\) 行，对于每次询问输出题目要求输出的值。

数据范围

\[对于 100\% 的数据，1\le n,m\le 5000,1\le q\le 3\times 10^5,1\le k\le 10^{14} \]

Solution

考虑从 \(S\) 串的每个位置开始，匹配一遍 \(T\) 串做出的贡献。例如对以下样例的两个串匹配：

3
abaab
abaabacaba
1
3
4

对于 \(S\) 串从第 \(1\) 个位置开始匹配，匹配一遍 \(T\) 串做出的贡献是一个子序列+\(S\) 的前三个字符。

这样可以 \(O(nm)\) 的预处理出来从 \(S\) 每个位置开始匹配一遍 \(T\) 做出的贡献。

然后完美可以把从每个位置开始匹配的状态看作一个点，由于从 \(1\) 开始匹配后做出的贡献是一个子序列+\(S\) 的前三个字符，故下一次匹配 \(T\) 的时候是从第 \(4\) 号位置开始匹配的，所以我们将 \(1\) 号点向 \(4\) 号点连一条单向边，同理我们可以建出来一个图。不难发现因为每一个点都有一条延申出去的单向边，故，此图存在一个环，如下图：

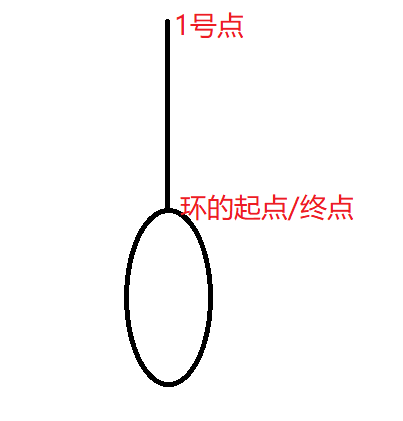
我们可以做一个类似于图上前缀和的东西，因为最初匹配是从 \(1\) 为起点开始匹配的，所以 \(1\) 号点作为根节点，然后做图上前缀和，前缀贡献。然后我们可以求出没有进入环的部分点数和环的部分点数。

对于每次询问 \(k\) 。我们可以分为两种种情况讨论

• \(k<没有进入环的部分的点数\)
• \(k > 进入环的部分点数\)

对于第二种情况，还要算最后环中余下点的贡献。

这么讲可能有点抽象，具体更具代码理解会更透彻。

CODE

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e3+7;
int Q;
int n,m;
string S,T;
int nxt[N],sum[N];
bool vis[N];
int pre_sum,nt_sum[N],lent,be,dep[N];
int num[N];
void dfs(int u,int dept){
    dep[u]=dept;
    num[dept]=num[dept-1]+sum[u];
    vis[u]=true;
    if(vis[nxt[u]]){
        be=dep[nxt[u]];
        lent=dept-be+1;
        pre_sum=num[be-1];nt_sum [0]=num[dept]-pre_sum;
        return;
    }
    dfs(nxt[u],dept+1);
    if(dept>=be){
        int ltt=dept-be+1;
        nt_sum[ltt]=num[dept]-pre_sum;
    }
}
signed main(){
    clock_t st,ed;
    st=clock();
    freopen("string.in","r",stdin);
    freopen("string.out","w",stdout);
    scanf("%lld",&Q);
    cin>>S>>T;
    n=S.length();m=T.length();
    for(int i=1;i<=n;++i){
        int idt=i-1;
        for(int j=1;j<=m;++j){
            if(S[idt%n]==T[j-1]){
                idt++;
            }
        }
        idt;
        sum[i]=(idt)/n;
        nxt[i]=(idt)%n+1;
    }
    dfs(1,1);
    while(Q--){
        int k;
        scanf("%lld",&k);
        int ans=0;
        if(k<be-1){
            printf("%lld\n",num[k]+1);
            continue;
        }
        else{
            ans+=pre_sum;k-=(be-1);
            ans+=(nt_sum[0]*(k/lent));
            k%=lent;
            if(k){
                ans+=nt_sum[k];
            }
            printf("%lld\n",ans+1);
        }
    }
    ed=clock();
    return 0;
}