牛客小白月赛60 题解
请您给个免费的【关注】和【点赞】，这对我真的很重要
前言
第二次小白月赛没有AK，感觉自己可以原地退役了QAQ。
这次F题理论上我能做出来，但是由于没有打表状态不佳，导致没有AK。
A.小竹与妈妈
思路
这题应该一眼题，不会的可以到小学重新学一遍了（）
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
int a,b,x;
signed main(){
cin>>a>>b>>x;
cout<<(x-b)/a;
return 0;
}
B.走丢的小竹
思路
同为一眼题，只要用个桶 a[i] 记录一下多少个管道通往 i，对于【询问操作】，直接输出 n-a[x] 即可。
代码
#include<bits/stdc++.h>
using namespace std;
int n,m,q;
int a[100010];
signed main(){
cin>>n>>m>>q;
for(int i=1;i<=n;++i){
int t;
cin>>t;
a[t]++;
}
while(q--){
int x;
cin>>x;
cout<<n-a[x]<<endl;
}
return 0;
}
C.小竹关禁闭
思路
一眼题，显然 \(O(n^2) 和 O(n)\) 都可以，但我一开始敲 \(O(n)\) 敲的有点急。。。所以挂了一发。
\(dp_i\) 为必选 \(i\) 点最优情况，然后枚举合法的上一个选择的物品 \(j\) ，然后用 \(dp_j\) 转移即可。
代码
#include<bits/stdc++.h>
using namespace std;
int n,k;
int dp[2010];
int a[2010];
signed main(){
cin>>n>>k;
for(int i=1;i<=n;++i){
cin>>a[i];
}
int ans=0;
for(int i=1;i<=n;++i){
int maxn=0;
for(int j=1;j<i-k;++j){
maxn=max(maxn,dp[j]);
}
dp[i]=a[i]+maxn;
ans=max(ans,dp[i]);
}
cout<<ans<<endl;
return 0;
}
D.游戏购买！
思路
比较显然的bfs题，直接从起点开始一遍bfs，记录从起点到图中每个点 \((i,j)\) 的距离 \(dist_{0,i,j}\) 。
然后从重点开始一遍bfs，记录从重点到图中每个点 \((i,j)\) 的距离 \(dist_{1,i,j}\)
答案就是对于每个满足 \(a_{i,j}>x\) 的点 \((i,j)\) ，取 一下\(dist_{0,i,j}+dist_{1,i,j}\) 的最小值即可。
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int,int>
int n,m,X;
int sx,sy,ex,ey;
int mp[2010][2010];
bool vis[2010][2010];
int dist[2][2010][2010];
int dx[]={0,1,0,-1},dy[]={1,0,-1,0};
signed main(){
scanf("%lld%lld%lld%lld%lld%lld%lld",&n,&m,&X,&sx,&sy,&ex,&ey);
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
scanf("%lld",&mp[i][j]);
}
}
memset(dist,0x3f,sizeof(dist));
queue<pii> qu;
qu.push(make_pair(sx,sy));
queue<int> qut;
qut.push(0);
vis[sx][sy]=true;
while(!qu.empty()){
pii pat=qu.front();
int dis=qut.front();
dist[0][pat.first][pat.second]=dis;
qu.pop();qut.pop();
for(int i=0;i<4;++i){
int xt=pat.first+dx[i],yt=pat.second+dy[i];
if(xt<1||xt>n||yt<1||yt>m) continue;
if(vis[xt][yt]||mp[xt][yt]==-1) continue;
vis[xt][yt]=true;
qu.push(make_pair(xt,yt));
qut.push(dis+1);
}
}
memset(vis,false,sizeof(vis));
vis[ex][ey]=true;
qu.push(make_pair(ex,ey));
qut.push(0);
while(!qu.empty()){
pii pat=qu.front();
int dis=qut.front();
dist[1][pat.first][pat.second]=dis;
qu.pop();qut.pop();
for(int i=0;i<4;++i){
int xt=pat.first+dx[i],yt=pat.second+dy[i];
if(xt<1||xt>n||yt<1||yt>m) continue;
if(vis[xt][yt]||mp[xt][yt]==-1) continue;
vis[xt][yt]=true;
qu.push(make_pair(xt,yt));
qut.push(dis+1);
}
}
int ans=0x3f3f3f3f;
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(mp[i][j]>X){
// cout<<i<<" "<<j<<":"<<dist[0][i][j]<<" "<<dist[1][i][j]<<endl;
ans=min(ans,dist[0][i][j]+dist[1][i][j]);
}
}
}
if(ans==0x3f3f3f3f) puts("-1");
else printf("%lld",ans);
return 0;
}
E.寻找小竹！
思路
显然这是一棵树，我们可以树形dp(假定1为树根)，对于一个路口 \(u\) 如果它的儿子 \(v\) 与它共同优雅，那么我们就 \(dp_u+=dp_v\) 即可。
这道题唯一的难点就在于如何判断两个路口为共同优雅。
错误做法：
最初我的判定方法就是在输入的时候用一个 vector 存一下每个 \(a_i\) 的质因子，然后在树形dp的过程中用双指针来确定是否共同优雅。由于每个数的质因子最多 \(log_2n\) 个。而质因数分解最坏是根号级的复杂度。所以我就觉得 4s 没问题，然后我就T了。。。
正确做法：
首先跑一遍素数筛，对于任意两个数 \(u\) 和 \(v\) ，如果 \(gcd(u,v)\) 不为素数，证明 \(u\) 和 \(v\) 至少有两个相同的质因数，但是这两个质因数不能保证互不相同。所以我们需要特殊判断 \(gcd(u,v)\) 是形如 \(x^y\) 的情况。
素数筛复杂度 \(O(n)\) ，预处理 \(x^y\) 的情况复杂度为 \(O(nlog_2n)\) 。树形dp复杂度 \(O(nlog_2n)\) ，总复杂度为 \(O(nlog_2n)\)。
代码
注释的代码为错误解法
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+7;
const int MAXN=5e6+7;
#define ll long long
int n,a[N];
vector<int> edge[N];
vector<int> b[N];
int siz[N];
int ans=1;
bool flt[MAXN];
bool prime[MAXN];
int primes[MAXN],cnt;
void get_primes2(int n) {
memset(prime, false, sizeof prime);
cnt = 0;
for (int i = 2; i <= n; i++) {
if (!prime[i]){
primes[cnt++] = i;
flt[i]=true;
}
for (int j = 0; primes[j] <= n / i; j++) {
prime[i * primes[j]] = true;
if (i % primes[j] == 0) break;
}
}
}
void init(){
flt[1]=true;
for(ll i=2;i<=MAXN-7;++i){
if(prime[i]) continue;
ll xt=1;
while(xt<=(ll)(MAXN)-7ll){
// cout<<xt<<endl;
flt[xt]=true;
xt*=i;
}
}
}
int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
void dfs(int u,int fa){
siz[u]=1;
for(int i=0;i<edge[u].size();++i){
int v=edge[u][i];
if(v==fa) continue;
dfs(v,u);
int xu=0,xv=0;
int cnt=0;
int gct=gcd(a[u],a[v]);
// cout<<gct<<" "<<flt[gct]<<endl;
if(!flt[gct]) siz[u]+=siz[v];
// while(xu<b[u].size()&&xv<b[v].size()){
// if(b[u][xu]==b[v][xv]){
// ++cnt;++xu;++xv;
// if(cnt>=2) break;
// }else if(b[u][xu]>b[v][xv]){
// ++xv;
// }else ++xu;
// }
// cout<<u<<" "<<v<<":"<<cnt<<endl;
// if(cnt>=2){
// siz[u]+=siz[v];
// }
}
ans=max(ans,siz[u]);
}
signed main(){
clock_t st,ed;
st=clock();
get_primes2(MAXN-7);
init();
ed=clock();
// cout<<ed-st<<endl;
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
int att;
// for(int j=2;j*j<=att;++j){
// if(att%j==0){
// while(att%j==0){att/=j;}
// b[i].push_back(j);
// }
// }
// if(a[i]>1) b[i].push_back(a[i]);
}
for(int i=1;i<n;++i){
int u,v;
scanf("%d%d",&u,&v);
edge[u].push_back(v);
edge[v].push_back(u);
}
dfs(1,0);
printf("%d",ans);
return 0;
}
F.被抓住的小竹
就是这道阴间的傻逼题让我emo了一晚上
思路
面对不会的数学题，记住打表很重要！！
这道题显然你只打最终答案的表看不出来规律，此时你打一下每种排列 \(p\) 的 \(H(p)\) 值。然后你就会惊人的发现，这是一个定值。
我打的表
0 1---0
0 5---1 5---5
0 15---1 15---1 15---2 15---2 15---3 15---135
0 35---1 35---1 35---2 35---2 35---3 35---1 35---2 35---2 35---3 35---3 35---4 35---2 35---3 35---3 35---4 35---4 35---5 35---3 35---4 35---4 35---5 35---5 35---6 35---2520
0 70---1 70---1 70---2 70---2 70---3 70---1 70---2 70---2 70---3 70---3 70---4 70---2 70---3 70---3 70---4 70---4 70---5 70---3 70---4 70---4 70---5 70---5 70---6 70---1 70---2 70---2 70---3 70---3 70---4 70---2 70---3 70---3 70---4 70---4 70---5 70---3 70---4 70---4 70---5 70---5 70---6 70---4 70---5 70---5 70---6 70---6 70---7 70---2 70---3 70---3 70---4 70---4 70---5 70---3 70---4 70---4 70---5 70---5 70---6 70---4 70---5 70---5 70---6 70---6 70---7 70---5 70---6 70---6 70---7 70---7
70---8 70---3 70---4 70---4 70---5 70---5 70---6 70---4 70---5 70---5 70---6 70---6 70---7 70---5 70---6 70---6 70---7 70---7 70---8 70---6 70---7 70---7 70---8 70---8 70---9 70---4 70---5 70---5 70---6 70---6 70---7 70---5 70---6 70---6 70---7 70---7 70---8 70---6 70---7 70---7 70---8 70---8 70---9 70---7 70---8 70---8 70---9 70---9 70---10 70---42000
然后通过打的表中 \(n=3,4\) 的情况，能大体才出来后半部分的通项公式为
\[\frac {n\times (n+1)\times (n+2)\times (n+3)}{24}
\]
我摊牌了，我就是不会具体证明。
upd:好耶我又会具体证明了！
具体证明
\[首先考虑求\sum^{n}_{x=1}\sum_{i=1}^{x}\sum_{j=x}^{n}f(p,i,j,x)
\]
然后考虑每一个区间的贡献，区间内每一个数作为 \(x\) 时，贡献是大于等于该数的个数。那么长度为 \(len\) 的区间贡献就为
\[\sum_{i=1}^{len}i=\frac{len\times (len+1)}{2}
\]
所以直接枚举区间长度，然后枚举起点,枚举起点为下文中的 \((n-len+1)\)
\[\sum_{len=1}^{n}(n-len+1)\frac{len\times (len+1)}{2}\\
=\frac{1}{2}\sum_{len=1}^{n}-len^3+nlen^2+(n+1)len\\
\]
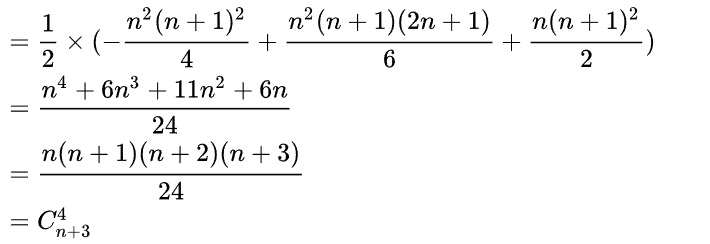
然后对于 \(inv(p)\) 的总和也是有通项公式的。【点我查看具体证明】
然后将 \(inv(p)\) 的总和和 \(H(p)\) 的总和求出来后乘起来，就AC了。注意除法要使用逆元。
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=1e9+7;
int T,n;
int a[100020];
int ksm(int x,int y){
int xt=x;
int res=1;
while(y){
if(y&1) res=(res*xt)%mod;
y>>=1;
xt=(xt*xt)%mod;
}
return res%mod;
}
int inv4;
signed main(){
inv4=ksm(4,mod-2);
a[0]=1;
for(int i=1;i<100010;++i){
a[i]=a[i-1]*i%mod;
}
cin>>T;
while(T--){
cin>>n;
int x1=n*(n-1)%mod*a[n]%mod*inv4%mod;
int x2=n*(n+1)%mod*(n+2)%mod*(n+3)%mod*ksm(24,mod-2)%mod;
cout<<x1*x2%mod<<endl;
}
return 0;
}
