奇怪的数据结构题(Trie树合并)
奇怪而又不算难的数据结构题
题面
题目描述
有一个集合 \(a\),初始为空。
你需要写一个数据结构,支持:
0 x表示将 \(x\) 加入该集合,其中 \(x\)为一数字串。保证 不在集合中。1 x表示查询 \(x\)是否存在于该集合中。2 x y表示令数字串 \(x\)和 \(y\)纠缠。不保证 \(x\)和 \(y\)在集合中。
另外,如果某数字串形如 \(x+z\)(\(+\) 为拼接操作),并且存在一数字串 \(x\)与\(y\) 纠缠,并且 \(y+z\)在集合中,则认为 \(x+z\)也在集合中。
注意集合中可能有无穷多个数字串。
输入格式
第一行一个正整数 \(m\),表示操作数。
接下来 \(m\)行,每行一个操作,具体见题目描述。
输出格式
对于每个 \(1\)操作,如果是输出 \(1\),否则输出 \(0\)。
样例输入
11
0 123
1 123
1 0
2 12 13
0 124
1 133
1 134
1 13
2 1 11
1 111
1 11111111111111111111111124
样例输出
1
0
1
1
0
0
1
数据范围
模拟赛中の奇怪遭遇吐槽
11/10的模拟赛十分傻逼诡异。T1 T3 T4全是数据结构阴间题,足以看出出题人多么傻逼牛逼。T1其实可以用set简单维护,但是我一时傻逼,觉得set肯定会寄(可能是我对stl不是那么敢用qwq)。然后就敲了250多行的线段树调了三个半小时。。。然后最后几分钟敲了T2的50分,导致我这次模拟赛考了两位数。。。
其实这题在并不难,我甚至感觉它比T1T2都简单。早知道就做T3了qwq
题解
对于插入和查询字符串是否存在的问题,不难想到是用Tire树。
显然的对于0和1操作可以直接用Tire来解决。
对于操作2这种纠缠操作,如果有写过后缀自动机和线段树合并的lao能轻松发现,可以利用类似后缀自动机的思路。让两个字符串纠缠就类似于后缀自动机fail指针的操作,具体操作如下。
我们知道对于Tire树上的每个点都代表一个字符串。
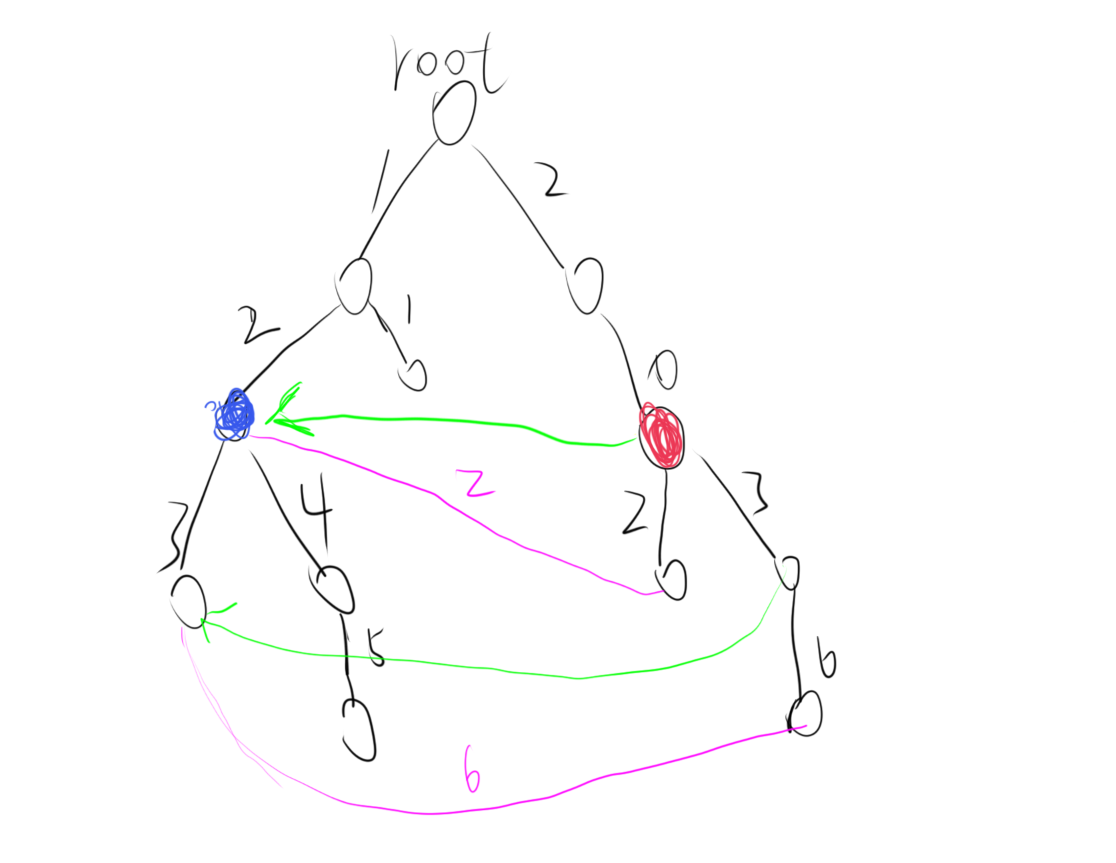
如下图。如果将12(蓝点)和20(红点)这两个串纠缠,就相当于把红点和蓝点并查集连边(绿色边,图中是将20合并入12)。
然后将这两颗子树进行类似线段树合并的操作(紫色边),相当于让并查集中所有点都可以连到并查集中其他点的儿子,注意合并过程中合并信息的同时还要进行并查集连边的操作以便于以后的合并。(灵魂画图)
个人认为这道题没有太大难点,就是合并操作有些特判需要注意,如下。
merge
合并操作代码:
void tir_merg(int &idx,int &idy){
idx=find(idx);
int fay=find(idy);
if(idx==fay) return;//如果两个串已经在一个并查集里,不需要合并直接返回
//合并过程中的操作,比较易懂
if(!idx){
idx=fay;
return;
}
else if(!idy){
idy=idx;
return;
}
fa[fay]=idx;
if(flt[fay]) flt[idx]=true;
for(int i=0;i<=9;++i){
tir_merg(tir[idx][i],tir[fay][i]);
idx=find(idx);
//注意如果出现类似样例中最后一组2的操作,可能会更新idx的并查集,所以每次需要更新当前的并查集。
}
}
完整代码
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
void read(int &ret){
int res=0,fs=1;
char a=getchar();
while(a<'0'||a>'9'){
if(a=='-') fs=-1;
a=getchar();
}
while(a>='0'&&a<='9'){
res=(res<<3)+(res<<1)+(a^48);
}
}
const int N=8e6+7;
int m;
int tir[N][10],rt=1,cnt=1;
char sx[N],sy[N];
bool flt[N];
int fa[N];
void init(){
for(int i=1;i<=N-6;++i){
fa[i]=i;
}
}
int find(int x){
return fa[x]==x ? x:fa[x]=find(fa[x]);
}
void insert(){
int len=strlen(sx);
int rtt=rt;
for(int i=0;i<len;++i){
int xt=sx[i]-'0';
if(!tir[rtt][xt]) tir[rtt][xt]=++cnt;
// cout<<rtt<<" "<<xt<<endl;
rtt=find(tir[rtt][xt]);
}
flt[rtt]=true;
}
void ask(){
int len=strlen(sx);
int rtt=rt;
for(int i=0;i<len;++i){
int xt=sx[i]-'0';
if(!tir[rtt][xt]){
puts("0");
return;
}
// cout<<rtt<<":"<<xt<<endl;
rtt=tir[rtt][xt];
rtt=find(rtt);
}
if(flt[rtt]) puts("1");
else puts("0");
}
int lenx,leny;
pii tir_get(){
pii res;
int rtt=rt;
for(int i=0;i<lenx;++i){
int xt=sx[i]-'0';
if(!tir[rtt][xt]) tir[rtt][xt]=++cnt;
rtt=find(tir[rtt][xt]);
}
res.first=rtt;
rtt=rt;
for(int i=0;i<leny;++i){
int xt=sy[i]-'0';
if(!tir[rtt][xt]) tir[rtt][xt]=++cnt;
rtt=find(tir[rtt][xt]);
}
res.second=rtt;
return res;
}
void tir_merg(int &idx,int &idy){
idx=find(idx);
int fay=find(idy);
if(idx==fay) return;
if(!idx){
idx=fay;
return;
}
else if(!idy){
idy=idx;
return;
}
fa[fay]=idx;
if(flt[fay]) flt[idx]=true;
for(int i=0;i<=9;++i){
tir_merg(tir[idx][i],tir[fay][i]);
idx=find(idx);
}
}
signed main(){
// freopen("tarjan.in","r",stdin);
// freopen("tarjan.out","w",stdout);
init();
clock_t S,E;
S=clock();
scanf("%d",&m);
while(m--){
int opt;
scanf("%d",&opt);
scanf("%s",sx);
if(opt==0){
insert();
}else if(opt==1){
ask();
}else{
scanf("%s",sy);
lenx=strlen(sx);leny=strlen(sy);
pii pat=tir_get();
tir_merg(pat.first,pat.second);
}
}
E=clock();
// cout<<"yzh's run:"<<E-S<<"ms"<<endl;
return 0;
}


