[SDOI2012]任务安排(山东省选)斜率dp
题目描述
机器上有 \(n\) 个需要处理的任务,它们构成了一个序列。这些任务被标号为 \(1\) 到 \(n\),因此序列的排列为 \(1 , 2 , 3 \cdots n\)。这 \(n\) 个任务被分成若干批,每批包含相邻的若干任务。从时刻 \(0\) 开始,这些任务被分批加工,第 ii 个任务单独完成所需的时间是 \(T_i\) 。在每批任务开始前,机器需要启动时间 \(s\),而完成这批任务所需的时间是各个任务需要时间的总和。
注意,同一批任务将在同一时刻完成。 每个任务的费用是它的完成时刻乘以一个费用系数 \(C_i\)。请确定一个分组方案,使得总费用最小。
输入格式
第一行一个整数 \(n\)。 第二行一个整数 \(s\)。接下来 \(n\) 行,每行有一对整数,分别为 \(T_i\) 和 \(C_i\),表示第 ii 个任务单独完成所需的时间是 \(T_i\) 及其费用系数 \(C_i\) 。
输出格式
一行,一个整数,表示最小的总费用。
输入输出样例
输入 #1
5
1
1 3
3 2
4 3
2 3
1 4
输出 #1
153
说明/提示
对于 \(100\%\) 数据,\(1 \le n \le 3 \times 10^5\) ,\(1 \le s \le 2^8\) ,\(\left| T_i \right| \le 2^8\) ,\(0 \le C_i \le 2^8\) 。
思路(注:结尾有完整AC代码,一定要看到最后!!!)
显然,\(n\)的最大值是\(3 \times 10^5\),暴力必然会炸
那么何为“斜率优化”呢?
答曰:用线性规划优化dp式。
顾名思义,斜率dp就是将题目给出的信息转换到坐标系中,判断斜率求解思路就这么讲完了 ,乍一看这个思路很突兀,那么我们来详细的进行分析。
首先我们根据提议可以得出这么个dp式子:
dp[i] = min(dp[i], dp[j] + tm[i] * (fm[i] - fm[j]) + (fm[n] - fm[j]) * s);
其中\(dp_i\)用来记录到\(i\)点为止的最优解,\(tm_i\)记录的是到\(i\)的\(t\)数组前缀和,\(f_i\)同理,\(j\)点只是中间的一个分割点,\(tm_i\times(fm_i-fm_j)\)是求这段区间的总耗费时间,最后一个式子至关重要,我们居然已经会在\(i\)这个为止分割一次,那么我们可以直接累加后面节点的\(s\)(机器启动耗费的时间)即为\((fm_n-fm_j)\times s\),这个思路是个人也能听懂
目前为止我们即可以得到:
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < i; ++j) {
dp[i] = min(dp[i], dp[j] + tm[i] * (fm[i] - fm[j]) + (fm[n] - fm[j]) * s);
}
}
这样写出来的代码即可以在洛谷得到20分,其他点全T掉。
显然,学过dp的人都能看出来,这个代码只是个普通的线性dp,那么接下来我们再利用这段代码推出斜率dp的代码。
通过上面的动态转移方程我们可以推出:
dp[i]=dp[j]-(tm[i]+s)fm[j]+tm[i]fm[i]+fm[n]*s;
拆开合并同类项而已,小学生也能推出来
学过斜率dp的大佬都能发现,这个式子符合函数的基本形式:\(y=kx+b\),我们将(tm[i]+s)看作k,将其余项看作b,既可以得出这个函数的斜率为(tm[i]+s)
这样我们就可以推出:对于每一个\(i\)我们都可以将dp[i]看作这个节点纵坐标,将fm[i]看作这个点的很坐标,于是我们可以将每个点放到坐标系中(非样例草图,有点难看凑活看吧):

那么我们再将函数图像带入坐标系中
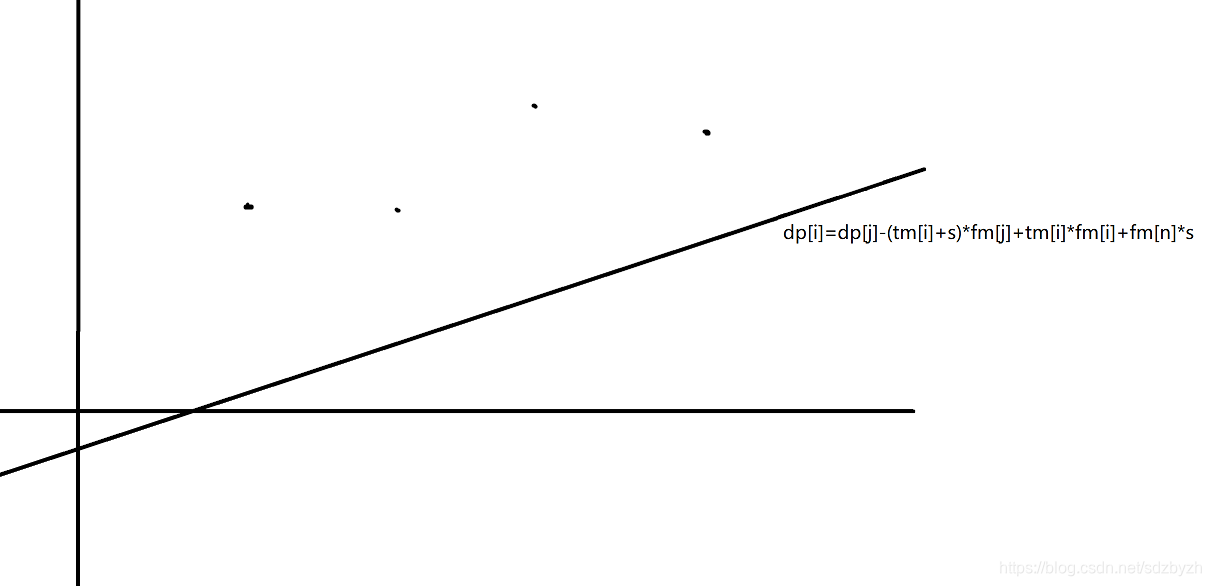
对于这条 dp[i]=dp[j]-(tm[i]+s)fm[j]+tm[i]fm[i]+fm[n]*s 的函数图像,要想球的dp最优解就要看这个函数图像先碰到哪个点,但是要将每个图像中的每个点进行比较那就太耗时间了,于是这里我们就会用到斜率的知识

红色的线连接的点为需要进行判断的点,上面那个蓝色的则是不需要判断的点。
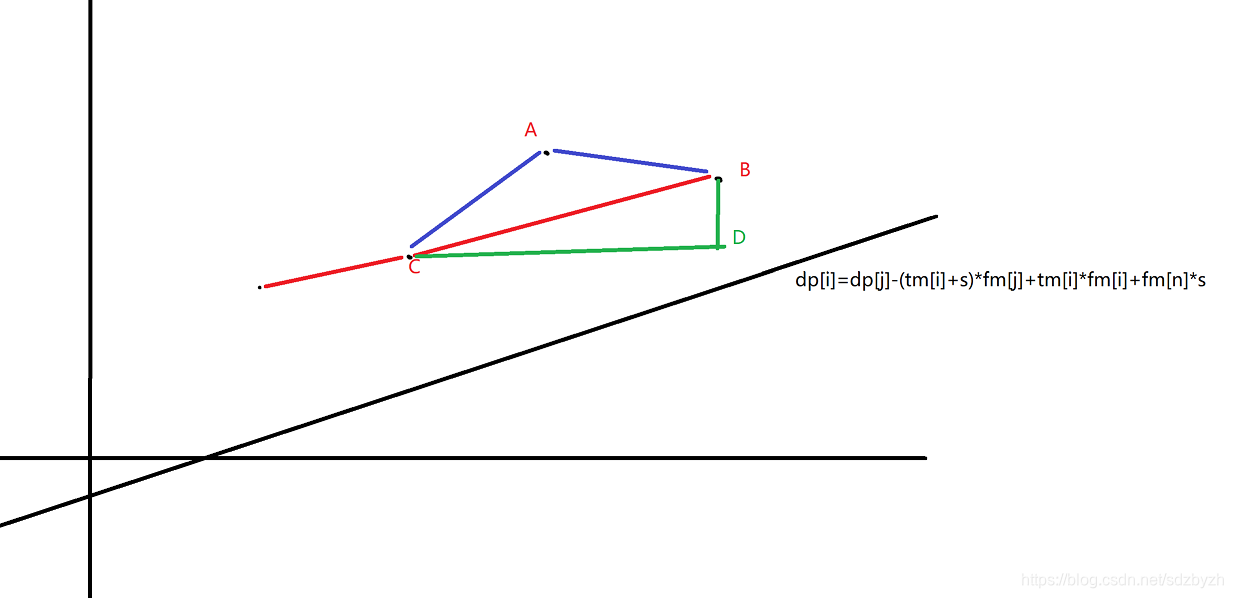
显然tan∠ACD > tan∠BCD(未学过tan点击次链接)
所以判断两点之间的斜率我们就只用判断对角边/斜边的值就可以了(\(CD=x_c-x_c\),\(BD=y_b-y_d\)),这里我们可以用队列来维护这些点(这段操作代码中很详细),所以针对每个\(i\),队列中每个tan的值就必须<=(tm[i]+s)(函数的斜率,之前讲过),然而在插入一个元素时就要从队尾倒着找到第一个tan>=tan(当前点)的值然而<=tan(当前点)的值就直接踢出队列,因为已经没有比较的必要了,于是到现在我们就可以得到斜率优化后的代码了:
for (int i = 1; i <= n; ++i) {
int j = 0;
while (l < r && dp[qu[l + 1]] - dp[qu[l]] <= (tm[i] + s) * (fm[qu[l + 1]] - fm[qu[l]]))
l++;
j = qu[l];
//dp[i] = min(dp[i], dp[j] - (s + tm[i]) * fm[j] + tm[i] * fm[i] + s * fm[n]);
dp[i] = dp[qu[l]] - (s + tm[i]) * fm[qu[l]] + tm[i] * fm[i] + s * fm[n];
//while(l<r&&)
while (l < r && (dp[qu[r]] - dp[qu[r - 1]])* (fm[i] - fm[qu[r]]) >= (dp[i] - dp[qu[r]]) * (fm[qu[r]] - fm[qu[r - 1]]))
r--;
qu[++r] = i;
}
注:代码中的判断用*是为了防止浮点运算
然而用了这个方法的oier会发现只能过\(60\%\)的点,其余点全WA,然而在我们之前的推到中忽略了和纵坐标(纵坐标具体数值前面已提过)为负数的情况
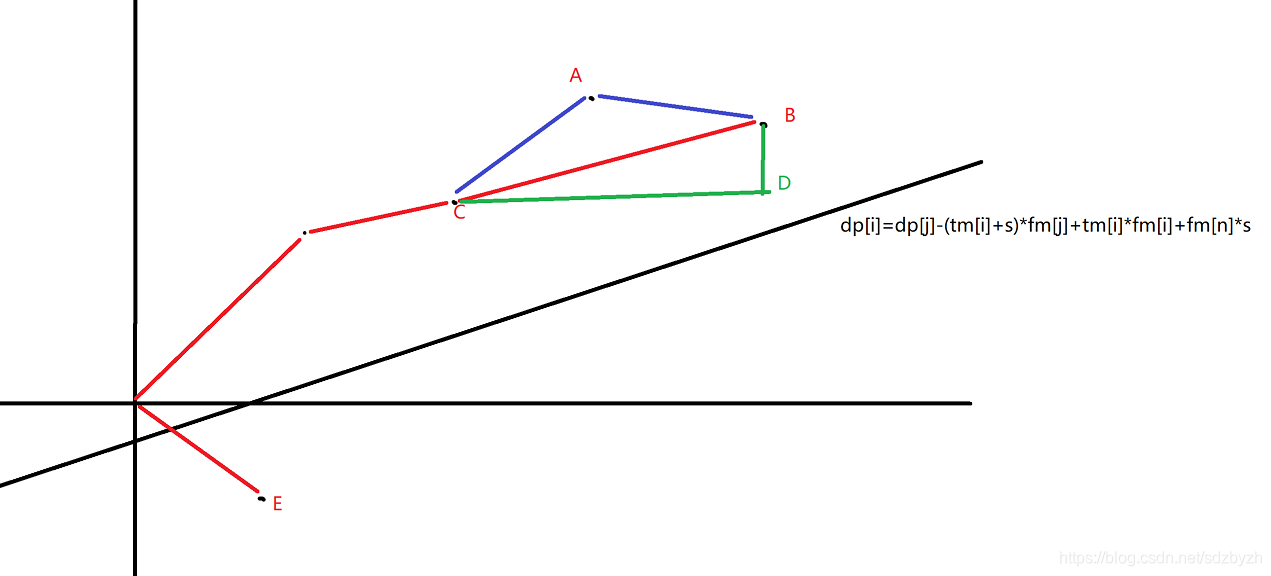
如图中的点E那么就会导致找最近点时,比较tan出锅了,于是,在第一个while循环中,我们改用二分的思路,整体思路和之前一样,直接上代码:
int bs(int ll, int rr, int ss) {//求j
int mid;
int res=qu[r];
while (ll <= rr) {
//l++;
mid = (ll + rr) / 2;
if (dp[qu[mid + 1]] - dp[qu[mid]] >= ss * (fm[qu[mid + 1]] - fm[qu[mid]])) {
res = qu[mid];
rr = mid - 1;
}
else
ll = mid + 1;
}
return res;
}
看到这里的oier们大概已经理解了,若还不理解可以结合完整代码进行理解:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
#pragma warning(disable:4996)
using namespace std;
#define int long long
int n, s, tm[1000010], fm[1000010], ans = 0x3f3f3f3f, dp[1000010], qu[1000010], l, r=0;
struct node
{
int t, f;
}edge[1000010];
int bs(int ll, int rr, int ss) {
int mid;
int res=qu[r];
while (ll <= rr) {
//l++;
mid = (ll + rr) / 2;
if (dp[qu[mid + 1]] - dp[qu[mid]] >= ss * (fm[qu[mid + 1]] - fm[qu[mid]])) {
res = qu[mid];
rr = mid - 1;
}
else
ll = mid + 1;
}
return res;
}
signed main() {
scanf("%lld%lld", &n, &s);
for (int i = 1; i <= n; ++i) {
scanf("%lld%lld", &edge[i].t, &edge[i].f);
tm[i] = tm[i - 1] + edge[i].t;
fm[i] = fm[i - 1] + edge[i].f;
}
memset(dp, 0x3f3f3f3f, sizeof(dp));
dp[0] = 0;
/*for (int i = 1; i <= n; ++i) {
for (int j = 0; j < i; ++j) {
dp[i] = min(dp[i], dp[j] + tm[i] * (fm[i] - fm[j]) + (fm[n] - fm[j]) * s);
}
}*/
//dp[i]=dp[j]-(tm[i]+s)*fm[j]+tm[i]*fm[i]+fm[n]*s;
qu[l] = 0;
qu[++r] = 0;
for (int i = 1; i <= n; ++i) {
int j = bs(l, r, (tm[i] + s));
dp[i] = dp[j] + tm[i] * (fm[i] - fm[j]) + s * (fm[n] - fm[j]);
while (l < r && (dp[qu[r]] - dp[qu[r - 1]])* (fm[i] - fm[qu[r]]) >= (dp[i] - dp[qu[r]]) * (fm[qu[r]] - fm[qu[r - 1]]))
r--;
qu[++r] = i;
}
cout << dp[n];
return 0;
}
各位读到最后的oier们点个赞吧qwq




