算法学习笔记(48)——状态压缩DP
状态压缩DP
蒙德里安的梦想
问题描述
求把 \(N×M\) 的棋盘分割成若干个 \(1×2\) 的长方形,有多少种方案。
例如当 \(N=2,M=4\) 时,共有 \(5\) 种方案。当 \(N=2,M=3\) 时,共有 \(3\) 种方案。
如下图所示:

输入格式
输入包含多组测试用例。
每组测试用例占一行,包含两个整数 \(N\) 和 \(M\)。
当输入用例 \(N=0,M=0\) 时,表示输入终止,且该用例无需处理。
输出格式
每个测试用例输出一个结果,每个结果占一行。
数据范围
$ 1 \le N,M \le 11$
输入样例:
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
输出样例:
1
0
1
2
3
5
144
51205
题目分析
题目描述中给定一个 \(N \times M\) 的棋盘,让我们将其分割成许多个 \(1 \times 2\) 的长方形,问总共有多少种分割的合法方案。等价的我们可以把这个分割的过程看作是如何通过合理摆放 \(1 \times 2\) 的小长方形,使得一块 \(N \times M\) 的面积刚好被这些相同大小的小长方形填满。自然而然产生的一个想法就是从左到右放置小长方形(更宽泛地可以说是从一头到另一头单向地摆放),这些小长方形要么是横着摆放的,要么是竖着摆放的,而在一个合法的方案中(即填满 \(N \times M\)),当我们确定了所有横着放的小长方形的位置之后,剩下的空位也必然能够恰好填入所有竖着放的小长方形,由此我们可以说,合法的方案数量等价于所有合法的横着摆放的小长方形的方案数量。
状态表示
-
集合:\(f[i][j]\) 表示前 \(i-1\) 列已经摆放完毕,且在第 \(i-1\) 列中横着放的小长方形伸到第 \(i\) 列的情况是 \(j\) 的所有方案的集合。
- 这里解释一下“情况是 \(j\) ”的含义,我们用一个二进制位表示一个位置上是否已摆放小长方形,若已摆放则是 \(1\),未摆放则是 \(0\),这样每一列的摆放情况都可以根据 \(n\) 个二进制位组成的一个数 \(j\) 来表示。例如第 \(i\) 列从上至下的摆放情况是"10100",于是就可以用对应的二进制数来代表这一列的摆放情况。
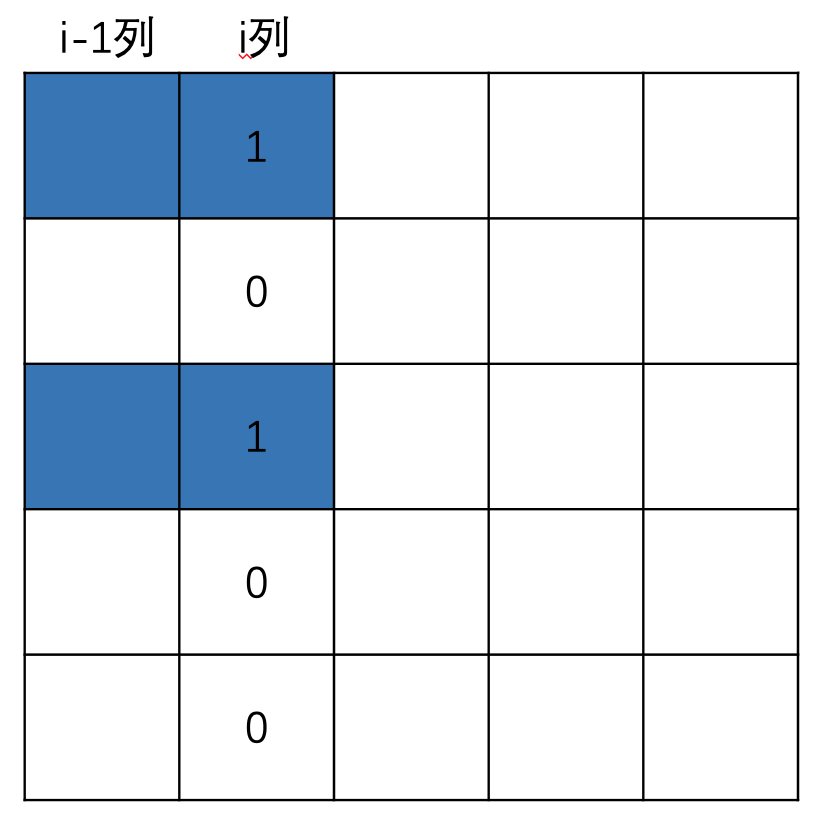
-
属性:方案数量的最大值。
状态转移
状态转移对应着集合划分,常见自然的思路是依据最后一步进行划分,这里我们的状态表示 \(f[i][j]\) 已经明确了第 \(i\) 列的摆放情况是 \(j\),那么我们就尝试根据此前的最后一步,即第 \(i-1\) 列的状态进行划分。仅仅依据第 \(i\) 列的情况,我们只能得知第 \(i-1\) 列中与右边伸出去的小长方形对应的左半部分的放置情况 \(j\),而不知道从第 \(i-2\) 列伸到第 \(i-1\) 列的情况,而这种情况可以用 \(f[i-1][k]\) 来表示,代表着前 \(i-2\) 列已摆放完毕,且从第 \(i-2\) 列伸出到 \(i-1\) 列的摆放情况是 \(k\) 的合法方案的数量,这时我们就需要判断哪些摆放方案能够使得两个过程不会产生冲突(一个是从 \(i-2\) 伸到 \(i-1\)的右半部分方案 \(k\),另一个是 \(i\) 中对应到 \(i-1\) 的左半部分方案 \(j\))。
针对这个问题,我们需要判断两点:
- \(k\) 与 \(j\) 不能重叠,即左边伸过来的和右边伸过来的不能重叠。
- 当前列中的空位必须是偶数个,否则没办法用竖着放的方式填满剩余位置。
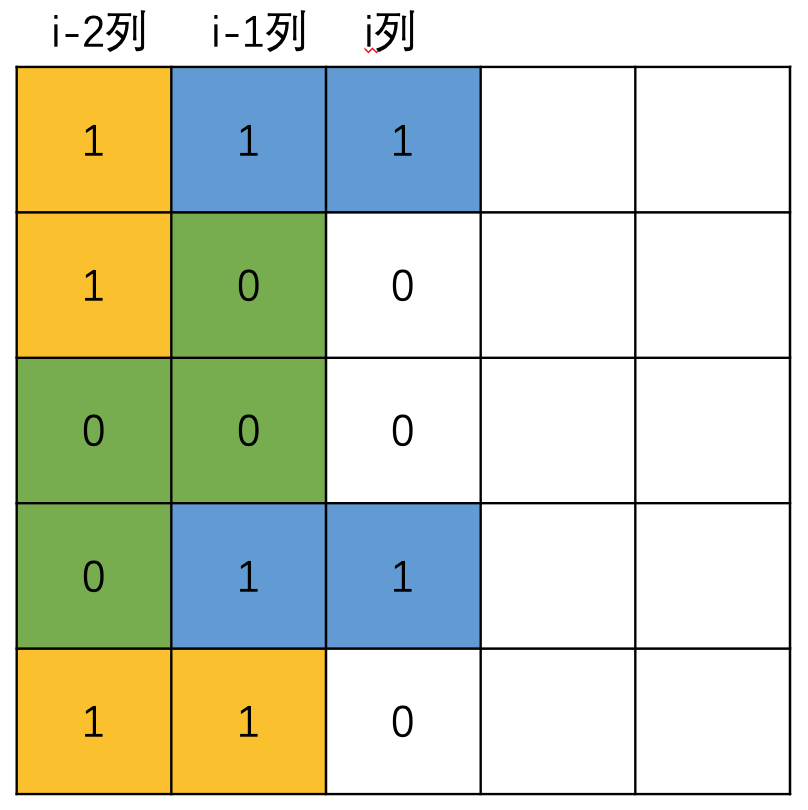
满足以上两点,针对每一个合法的 \(k\) 到 \(j\) 的转移,有如下状态转移方程:
代码实现
具体的代码实现中,我们对所有可能的状态进行预处理,is_Valid_State[]数组表示每个方案留下的空位是否是偶数个。state[]数组保存每个状态对应的合法的上一状态(即满足前面提到的两个条件,不叠加摆放和偶数个空位)。
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
using LL = long long;
const int MAX_N = 12, MAX_ST = 1 << MAX_N;
int N, M;
LL f[MAX_N][MAX_ST];
vector<int> state[MAX_ST];
bool is_Valid_State[MAX_ST];
int main()
{
while (cin >> N >> M, N || M) {
// 预处理合法状态(不能有奇数个空位)
for (int i = 0; i < 1 << N; ++ i) {
bool is_valid = true; // 标记状态合法性
int cnt = 0; // 统计0的个数
for (int j = 0; j < N; ++ j) {
if (i >> j & 1) {
// 1 & 1 = 1, 2 & 1 = 0
if (cnt & 1) {
is_valid = false;
break;
}
cnt = 0;
}
else {
++ cnt;
}
}
// 特判最后一位是0的情况
if (cnt & 1) is_valid = false;
is_Valid_State[i] = is_valid;
}
// 预处理出每一个方案合法的上一状态
for (int i = 0; i < 1 << N; ++ i) {
state[i].clear();
for (int j = 0; j < 1 << N; ++ j)
// 注意:==的优先级高于&,所以加括号
if ( (i & j) == 0 && is_Valid_State[i | j] )
state[i].push_back(j);
}
memset(f, 0, sizeof f);
f[0][0] = 1; // 什么都不放是一种合法方案,其余方案初始化为0
// 枚举每一列
for (int i = 1; i <= M; ++ i)
// 枚举每一个状态
for (int j = 0; j < 1 << N; ++ j) {
for (auto k : state[j])
f[i][j] += f[i - 1][k];
}
cout << f[M][0] << endl;
}
return 0;
}
最短Hamilton路径
问题描述
给定一张 \(n\) 个点的带权无向图,点从 \(0∼n−1\) 标号,求起点 \(0\) 到终点 \(n−1\) 的最短 Hamilton 路径。
Hamilton 路径的定义是从 \(0\) 到 \(n−1\) 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 \(n\)。
接下来 \(n\) 行每行 \(n\) 个整数,其中第 \(i\) 行第 \(j\) 个整数表示点 \(i\) 到 \(j\) 的距离(记为 \(a[i,j]\))。
对于任意的 \(x,y,z\),数据保证 \(a[x,x]=0,a[x,y]=a[y,x]\) 并且 \(a[x,y]+a[y,z]\ge a[x,z]\)。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
数据范围
\(1 \le n \le 20\)
\(0 \le a[i,j]\le 10^7\)
输入样例:
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例:
18

#include <iostream>
#include <cstring>
using namespace std;
const int MAX_N = 21, MAX_POINT = 1 << MAX_N;
int n;
int w[MAX_N][MAX_N];
int f[MAX_POINT][MAX_N];
int main()
{
cin >> n;
for (int i = 0; i < n; ++ i)
for (int j = 0; j < n; ++ j)
cin >> w[i][j];
/*
* 初始化:
* 初始状态经过的点只有0,所以只有0这一位是1,且当前位于点0的最短距离是0;
* 由于求的是最短路径,所以其余状态初始化为正无穷;
*/
memset(f, 0x3f, sizeof f);
f[1][0] = 0;
// 枚举每一种可能的路径方案i
for (int i = 0; i < 1 << n; ++ i)
// 枚举每一个终点j
for (int j = 0; j < n; ++ j)
// 如果当前枚举到的方案能够到达点j
if (i >> j & 1)
// 枚举每一个可能到达点j的前驱k
for (int k = 0; k < n; ++ k)
// 如果点k能够到达点j
if ( (i ^ (1 << j)) >> k & 1)
// 状态更新
f[i][j] = min(f[i][j], f[i ^ (1 << j)][k] + w[k][j]);
// 最后答案是经过了所有点,且终点是n-1号点的最短Hamilton路径的距离
cout << f[(1 << n) - 1][n - 1] << endl;
return 0;
}

