算法学习笔记（41）——容斥原理

容斥原理

设 $S_1,S_2,\cdots,S_n$ 为有限集合，$|S|$ 表示集合 $S$ 的大小，则：

$$\vert \bigcup\limits_{i=1}^{n}S_i \vert = \sum\limits_{i=1}^{n} \vert S_i \vert - \sum\limits_{1 \le i \le j \le n} \vert S_j \cap S_j \vert + \sum\limits_{1 \le i \le j \le k \le n} \vert S_j \cap S_j \cap S_k \vert + \dots + (-1)^{n+1} \vert S_1 \cap \dots \cap S_n \vert$$

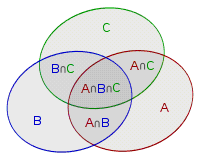
可以用文氏图来宏观地描述容斥原理，如下图所示：

组合数的性质：

$$C_n^0 + C_n^1 + C_n^2 + \dots + C_n^n = 2^n$$

从n个数里面挑0个数的方案数，加上挑1个数的方案数...，一直加到挑n个数的方案数，等价于从n个数中选任意多个数，每个数都是挑或不挑的所有方案数。
所以 $C_n^1 + C_n^2 + \dots + C_n^n = 2^n - 1$，共有 $2^n-1$ 项，时间复杂度为 $O(2^n)$

题目链接:AcWing 890. 能被整除的数

1. 每个集合实际上并不需要知道具体元素是什么，只要知道这个集合的大小，大小为$\vert S_i \vert = \frac{n}{p_i}$
2. 交集的大小如何确定？因为 $p_i$ 均为质数，这些质数的乘积就是他们的最小公倍数，$n$ 除这个最小公倍数就是交集的大小，故 $\vert S_1 \cap S_2 \vert = \frac{n}{p1 \cdot p2}$
3. 如何用代码表示每个集合的状态？这里使用的二进制，位运算枚举所有方案，从 $1$ 枚举到 $2^n-1$，用每一个数代表一种选法（二进制形式）。以 $m = 4$ 为例，所以需要 $4$ 个二进制位来表示每一个集合选中与不选的状态，$\overbrace{1101}^{m=4}$ ,这里表示选中集合 $S1,S3,S4$ ，故这个集合中元素的个数为 $\frac{n}{p1 \cdot p3 \cdot p4}$, 因为集合个数是 $3$ 个，根据公式，前面的系数为 $(−1)^{3−1} = 1$。所以到当前这个状态时，应该是 $res = res + \frac{n}{p1 \cdot p3 \cdot p4}$ 。这样就可以表示的范围从 $0000$ 到 $1111$ 的每一个状态

用二进制表示状态的小技巧非常常用，后面的状态压缩DP也用到了这个技巧，因此一定要掌握

C++程序1s内可以计算 $10^7$ ~ $10^8$ 次，本题中 $2^m = 2^{16} = 65536$，不会超时。
$1$ ～ $n$ 中 $p$ 的倍数的个数是 $\lfloor \frac{n}{p} \rfloor$

时间复杂度：$O(m2^m) = O(16\times2^{16}) \approx 1,000,000$

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 20;
int n, m;
int primes[N];

int main()
{
    cin >> n >> m;
    for (int i = 0; i < m; i ++ ) cin >> primes[i];
    
    int res = 0;    //  用于存储结果（满足条件的整数个数）
    
    // 枚举从1到2^n - 1(111...1)的数，代表所有的选择方案
    for (int i = 1; i < 1 << m; i ++ ) {
        int t = 1;  // 存储当前选择方案里的质数的乘积
        int s = 0;  // 存储选中的方案的数量,根据奇偶决定正负号
        
        // 枚举当前方案的每一位，1表示当前方案选择了当前位的数字，0表示没有选择
        for (int j = 0; j < m; j ++ ) {
            // 如果当前为数字是1，代表选择了该数字
            if (i >> j & 1) {
                // 乘积大于n，则 n/p[0]*...*p[j] = 0，则n被分母的几个质数整除的交集大小是0
                if ((LL)t * primes[j] > n) {
                    t = -1; // 标记当前方案不符合，跳出循环，判断下一方案
                    break;
                }
                s ++;       // 统计当前方案内的数字个数
                t *= primes[j];
            }
        }
        
        if (t == -1) continue;
        
        // 二进制末尾是1则为奇数，等价于s % 2 != 0
        if (s & 1) res += n / t;
        else res -= n / t;
    }
    
    cout << res << endl;
    
    return 0;
}