算法学习笔记（24）——拓扑排序

拓扑排序

计算拓扑序列的一个方式是，用BFS来尝试访问所有的节点，但是有一个约束就是只有入度为0的节点才能被加入到扩展队列里。每次从队列里取出一个节点，也就同时在图中将这个节点拆除，所以它的所有后继的节点都减少1，如果已经减少到0，那么就可以加入到队列中。

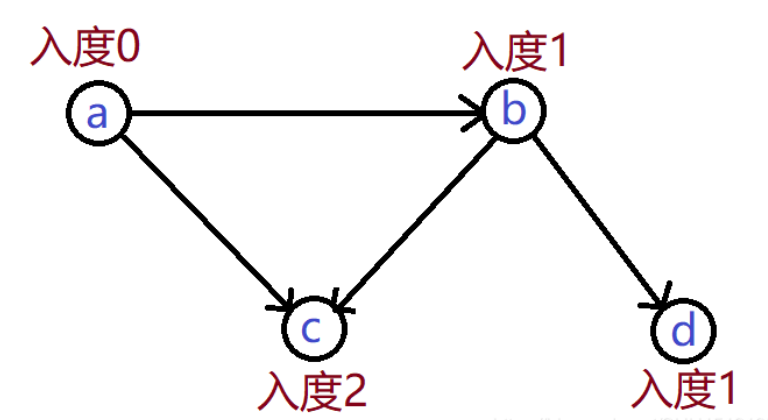
在上面的例子中，一开始只有a的入度是0，所以先把a加入到队列中，队列中：

a

然后取出队头a并在图中拆除，然后它的后继c的入度变成1，b的入度变成0，把b加入到队列里，队列中：

b

然后取出队头b bb并在图中拆除，然后它的后继c和d的入度都变成0，都加入到队列里，队列中是：

c d

或者

d c

接下来也是重复这个过程，最后得到拓扑序列是a b c d或者a b d c（取决于c和d哪个先从“d的所有后继”这个集合中访问）。

题目链接:AcWing 848. 有向图的拓扑序列

利用BFS寻找拓扑序列时，我们需要申请一个队列，而STL的queue每次拓展搜索后会让前一节点出队，不能保存下来，需要另外开一个数组存储拓扑序列，所以为了节省空间，我们这里选择利用数组模拟队列，只需移动头尾指针模拟入队与出队操作，而不是真正意义上的出队（删除元素），所以宽搜结束后数组内的元素就是一个拓扑序列。

还需注意一点，初始化队列时需要将所有入度为0的节点入队，从单一节点出发可能会找不到拓扑序列

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], e[N], ne[N], idx;
int q[N], d[N]; // q存储拓扑序列，d存储每个点的入度

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

bool topsort()
{
    int hh = 0, tt = -1; // 初始化头尾指针
    
    // 将所有度数为0的节点入队
    for (int i = 1; i <= n; i ++ )
        if (d[i] == 0) q[++ tt] = i;
    
    // 宽搜套路
    while (hh <= tt) {
        int t = q[hh ++];
        
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            // 删去出队节点与其相邻节点的边，相邻节点的入度减一
            d[j] --;
            // 如果相邻节点的入度减为0，则可以加入拓扑序列
            if (d[j] == 0) q[++ tt] = j;   
        }
    }
    
    // 由于tt从0开始计数，所以判断其是否等于n来确定是否所有点都加入了拓扑序列
    return tt == n - 1;
}

int main()
{
    memset(h, -1, sizeof h);
    
    cin >> n >> m;
    
    while (m -- ) {
        int x, y;
        cin >> x >> y;
        add(x, y);      // 添加一条由x到y的有向边
        d[y] ++;        // y的入度 + 1
    }
    
    // 如果存在拓扑序列
    if (topsort()) {
        for (int i = 0; i < n; i ++ ) cout << q[i] << ' ';
    }
    // 如果不存在拓扑序列
    else
        puts("-1");
    
    return 0;
}