算法学习笔记（19）——堆（heap）

堆

堆是一种数据结构，主要包含以下操作：

1. 插入一个数：将该数插到最后的位置，进行一次up操作
2. 求集合中的最小值：输出堆顶元素
3. 删除任意一个元素：将要删除的元素与末尾元素交换，然后进行一次up和down操作
4. 修改任意一个元素：将某位置的元素修改，然后进行一次up和down操作
5. 删除最小值：交换堆顶元素与末尾元素，进行一次down操作

堆排序

题目链接:AcWing 838. 堆排序

堆中某节点的编号 \(n\) 的左子节点编号是 \(2n\)，右子节点编号是 \(2n+1\)。
本题只需从小到大输出数列元素，所以只需要实现down操作，确保从小到大的排序即可。

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], cnt; // h[N]存储堆，cnt表示堆中元素个数

// 对下标为u的节点进行down操作
void down(int u)
{
    // 用t存储左右孩子节点与父节点中最小的下标
    int t = u;
    // 判断左孩子节点是否更小且下标合法
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    // 判断右孩子节点是否更小且下标合法
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (t != u) {
        swap(h[u], h[t]);
        down(t);
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> h[i];
    cnt = n;
    
    // 从第一个非叶子结点开始进行down操作
    for (int i = n / 2; i; i -- ) down(i);
    
    while (m -- ) {
        // 每次输出堆顶元素后便删除该元素，再经过down操作即可获得剩余部分的最小元素
        cout << h[1] << ' ';
        swap(h[1], h[cnt --]);
        down(1);
    }

    return 0;
}

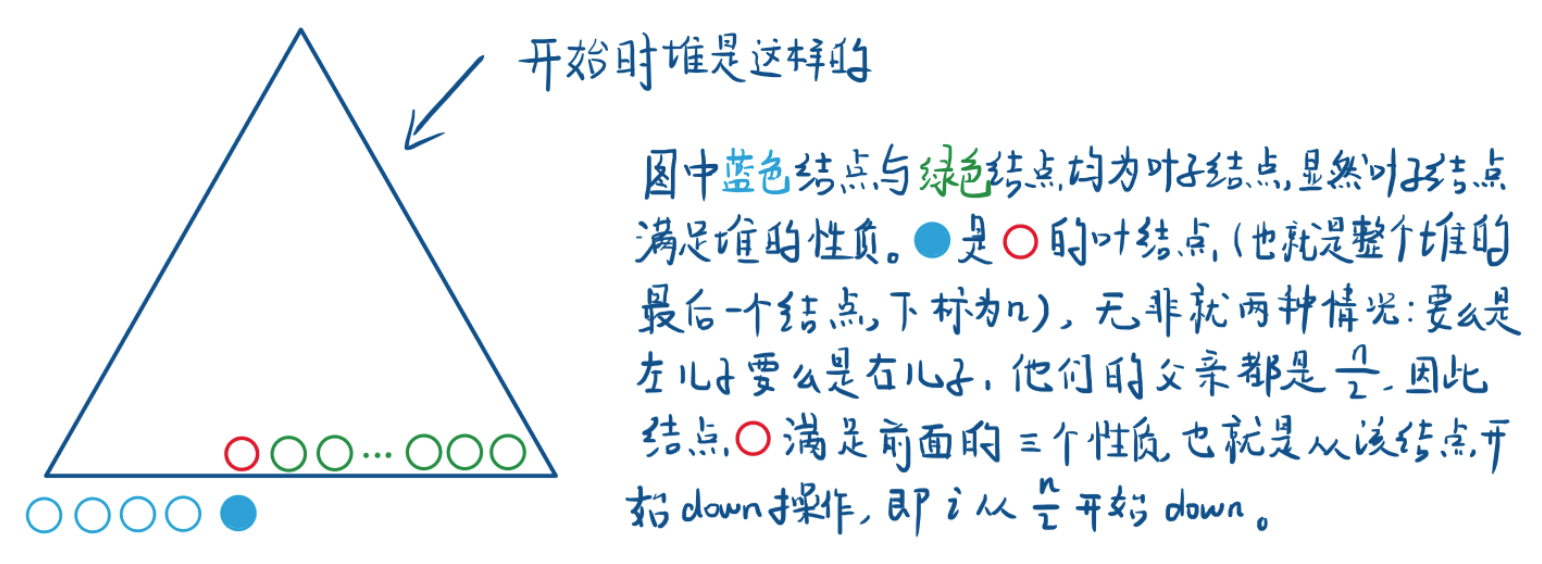
\(i\) 为什么从 \(n/2\) 开始down？

首先要明确要进行down操作时必须满足左儿子和右儿子已经是个堆。

开始创建堆的时候，元素是随机插入的，所以不能从根节点开始down，而是要找到满足下面三个性质的结点：

1. 左右儿子满足堆的性质。
2. 下标最大（因为要往上遍历）
3. 不是叶结点（叶节点一定满足堆的性质）

那这个点为什么时 \(n/2\) ？看图:

如果采用插入式建堆，则时间复杂度是 \(O(n\log n)\) ，从 \(\frac{n}{2}\) 开始down操作建堆的时间复杂度是 \(O(n)\).

模拟堆

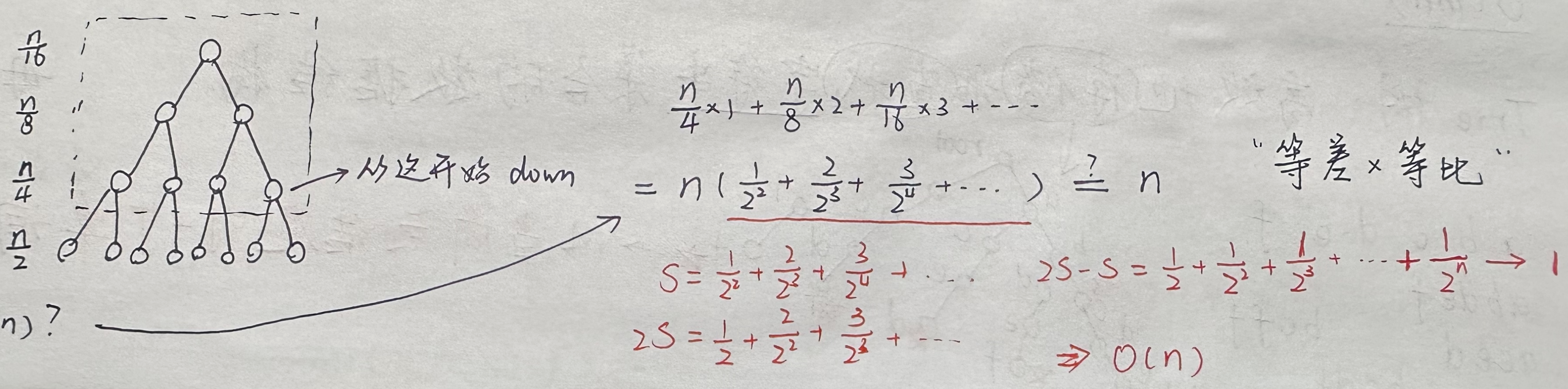
题目链接:AcWing 839. 模拟堆

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

/*
 * h[N] : 堆
 * hp[N]: 记录堆中编号为k的节点是第几次插入的
 * ph[N]: 记录第k次插入的节点在堆中编号是多少
 * cnt  : 堆中的节点数量
 * m    : 总的插入次数
 */
int n;
int h[N], hp[N], ph[N], cnt, m;

// 交换堆中编号为a和b的节点的值
void heap_swap(int a, int b)
{
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (t != u) {
        heap_swap(t, u);
        down(t);
    }
}

void up(int u)
{
    while (u / 2 && h[u / 2] > h[u]) {
        heap_swap(u / 2, u);
        u >>= 1;
    }
}

int main()
{
    cin >> n;
    while (n -- ) {
        string op;
        int k, x;
        cin >> op;
        if (op == "I") {
            cin >> x;
            cnt ++, m ++;
            ph[m] = cnt, hp[cnt] = m;
            h[cnt] = x;
            up(cnt);
        }
        else if (op == "PM") cout << h[1] << endl;
        else if (op == "DM") {
            heap_swap(1, cnt --);
            down(1);
        }
        else if (op == "D") {
            cin >> k;
            k = ph[k];
            heap_swap(k, cnt --);
            up(k), down(k);
        }
        else {
            cin >> k >> x;
            k = ph[k];
            h[k] = x;
            up(k), down(k);
        }
    }
    return 0;
}