Applied Cryptography（4）——非对称加密系统（Asymmetric Cryptosystems）

非对称加密系统(RSA)

非对称加密系统(RSA)

非对称加密系统（Asymmetric Cryptosystems）

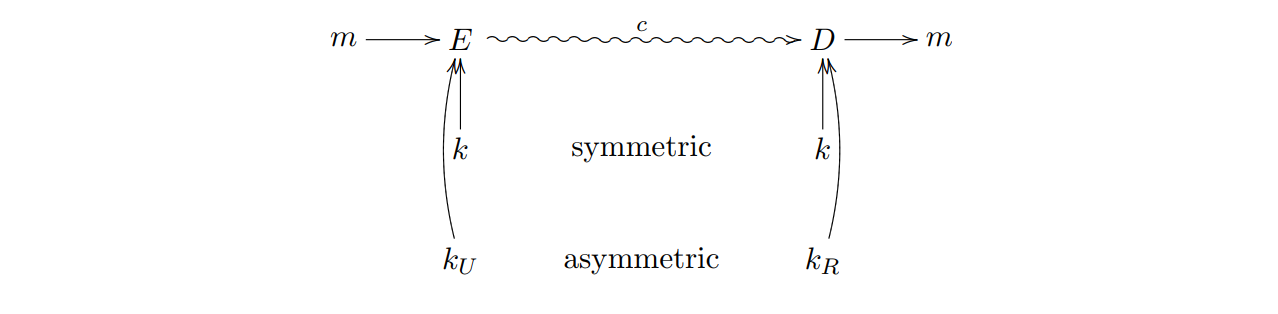
非对称加密系统（公钥用于加密，私钥用于解密）：

\[D_{kRB}(E_{kUB}(m))=m \]

RSA加密算法是首个非对称加密算法，由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）在1977年一起提出的。当时他们三人都在麻省理工学院工作。RSA 就是他们三人姓氏开头字母拼在一起组成的。

本节主要从以下几方面进行学习：

RSA
Using RSA in practice
Applications

数字签名（Digital Signature）

非对称加密系统的应用之一

Alice利用她的私钥($k_{RA}$)加密签名，Bob用Alice的公钥($k_{UA}$)进行解密，证实该消息确实是由Alice本人发送的。

\[E_{kUA} (D_{kRA}(m)) = m \]

RSA加密系统

陷门函数（"Trap door" one-way function）

在理论计算机科学和密码学中，陷门函数是一种在一个方向上很容易计算，但在没有特殊信息的情况下很难在相反方向上计算（寻找它的逆）的函数，称为“陷门”。陷门函数是单向函数的一种特殊情况，广泛用于公钥密码学中。Diffie & Hellman (1976)创造了这个术语。已经提出了几个函数类，很快就发现陷门函数比最初想象的更难找到。

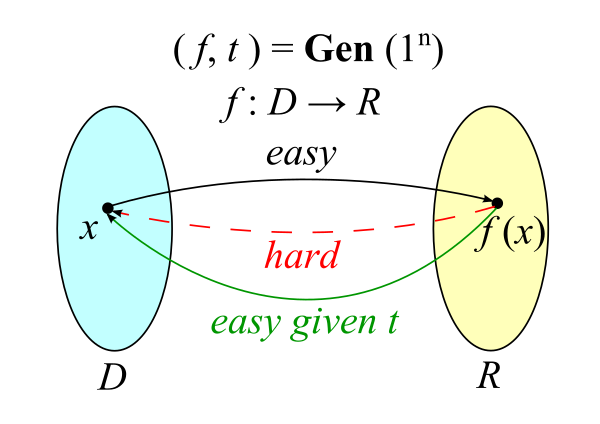
RSA是第一个具有该属性的加密系统。

RSA Cryptosystems names after Rivest, Shamir and Adleman is the most famous asymmetric cryptosystem used worldwide.
It works as follows:

The public key is a pair of 2 numbers: $k_U = (e; n)$ where $n = p · q$ the product of 2 large prime numbers and $e$ is a secret number.
The secret key is a pair of 2 numbers: $k_R = (d; n)$ where $n$ is the modulus as before and $d$ is a secret number.
To perform encryption fo some message $m$:
\[E_{k_U} (m) = m^e \bmod n \]
To perform decryption on a ciphertext $c$ using the secret key $k_R$:
\[D_{k_R}(c) = c^d \bmod n \]

如何选择$e, d, n$的值？

RSA的正确性

RSA正确即需证明一条消息能够加密解密后复原，则需要满足：

\[D_{k_R}(c) = c^d \bmod n = (m^e \bmod n)^d \bmod n = m^{ed} \bmod n = m \]

即我们的目标是选择合适的 $e,d,n$ ，使其满足：

\[\forall m \in \mathbb{Z}, m^{ed - 1} \equiv 1 \bmod n \]

如何选择合适的 $e,d,n$，首先需要知道欧拉定理(Euler's Theorem)

欧拉定理(Euler's Theorem)

\[if \ \ gcd(a, n) = 1 \\ a^{\varphi(n)} \equiv 1 \bmod n \]

欧拉函数(Totient function) $\varphi (n) $

在数论中，对正整数n，欧拉函数 $\varphi (n)$ 是小于等于 $n$ 的正整数中与 $n$ 互质的数的数目。
如果 $n$ 是一个质数，则 $\varphi (n) = n - 1$ .
如果 $n = pq$ ，并且 $p, q$ 均为质数，则：

\[\varphi (n) = pq - 1 - (q - 1) - (p - 1) = pq - (p + q) + 1 = (p - 1)(q -1) = \varphi(p)\varphi(q) \]

证明欧拉定理

\[a^{\varphi (n)}\equiv 1\pmod n \]

即 $a^{\varphi (n)}$ 与 $1$ 在模 $n$ 下同余；$\varphi(n)$ 为欧拉函数。

费马小定理（Fermat's little theorem）

假如 $a$ 是一个整数，$n$ 是一个质数，那么 $a^{n}-a$ 是 $n$ 的倍数，可以表示为:

\[a^{n}\equiv a{\pmod {n}} \]

如果 $a$ 不是 $n$ 的倍数，这个定理也可以写成更加常用的一种形式:

\[a^{{n-1}}\equiv 1{\pmod {n}} \]

费马小定理的证明：
考虑在 $gcd(a, n) = 1$ 时的一组数：

\[\lbrace a \bmod n, 2a \bmod n, ... , (n - 1)a \bmod n \rbrace = \lbrace r_1, r_2, ... , r_{n - 1} \rbrace \]

则 $\lbrace r_1, r_2, ... , r_{n - 1} \rbrace$ 为集合 $\lbrace 1, 2, ... n - 1 \rbrace$ 的重新排列，即 $1,2,...,n-1$ 在余数中恰好出现一次。这是因为对于任意两个相异的 $k*a(k = 1, 2,...n-1)$，它们的差不是 $n$ 的倍数，所以不会有相同的余数，且任一 $k*a$ 也不是 $n$ 的倍数，所以余数不为 $0$，因此：

\[1\cdot2\cdot3...(n-1) \equiv (1\cdot a)\cdot (2\cdot a)\cdot \dots \cdot ((n-1)\cdot a) \pmod n \\ (n-1)! \equiv (n-1)! a^{n-1}\pmod n\\ a^{n-1} = 1 \pmod n \]

至此，费马小定理为：$a^{n-1} \equiv 1 \bmod n$
但是我们还需要证明：$a^{\varphi (n)}\equiv 1\bmod n$

Case1 : $n$ 是一个质数，则 $\varphi(n) = n - 1$，利用费马小定理即可证明
Case2 : $n$ 不是质数，且 $a$ 与 $n$ 互质
定义集合 $\mathbb{R}$ 是与 $n$ 互质的数 $x(x < n)$ 的集合
\[\mathbb{R} = \lbrace x_1, x_2, ..., x_r \rbrace \\ \mathbb{S} = \lbrace ax_1 \bmod n, ax_2 \bmod n, ... ,ax_r \bmod n \rbrace \]
由欧拉函数的定义可知，$\mathbb{R}$ 数组的大小就是 $\varphi(n)$ 的值，即 $|R| = \varphi(n)$。
由于 $a$ 与 $n$ 互质，所以不存在 $i \neq j$ 使得 $ax_i \bmod n = ax_j \bmod n$，即 $\mathbb{S}$ 数组内的元素各异，且 $\mathbb{S}$ 数组与 $\mathbb{R}$ 数组大小相同（和 $n$ 互质的数只有 $\varphi(n)$ 个），且数组 $\mathbb{S}$ 内的每一元素也与 $n$ 互质，所以 $\mathbb{S}$ 数组与 $\mathbb{R}$ 数组具有相同的元素，则 $\mathbb{S}$ 数组是 $\mathbb{R}$ 数组的重新排列。则：
\[\prod(R) = x_1 \cdot x_2\ ...\ x_r = ax_1 \bmod n \cdot ax_2 \bmod n\ ...\ ax_r \bmod n \\ x_1 \cdot x_2\ ...\ x_r = a^{\varphi(n)}(x_1 \cdot x_2\ ...\ x_r) \bmod n \\ a^{\varphi(n)} \equiv 1 \bmod n \]

证毕

再回到RSA...

RSA加密算法我们需要选择两个大的质数 $p$ 和 $q$，$p \neq q$，计算 $n = pq$

公钥：$k_U=(e;n)$
私钥：$k_R=(d;n)$
加密函数：$E_{k_U}(m) = m^e \bmod n$
解密函数：$D_{k_R}(m) = c^d \bmod n$
可逆性（Invertibility）： $m^{ed-1} \equiv 1 \bmod n$

由欧拉定理：$a^{\varphi(n)} = 1 \bmod n$，$a$ 与 $n$ 互质，则我们需要找出一组 $e$ 和 $d$，使得 $k*\varphi(n) = ed - 1$，又因为 $n = pq$，则 $\varphi(n) = \varphi(p) \varphi(q) = (p-1)(q-1)$，即上式为：

\[ed - 1 = k(p-1)(q-1) \]

由于我们希望私钥更加保密且难以被攻击者猜测，所以我们应该随机选择 $d$ 的值（私钥中包含 $d$ ）。而 $e$ 则是可以公开的，实际上，$e$ 常常被赋予一个较小的值

随机选择一个 $d$ 使得其与 $\varphi(n)$ 互质，则

\[de = 1 \bmod \varphi(n) \]

Q：已知 $d$ 和 $\varphi(n)$ 的前提下，计算 $e$ 困难吗？
A：不困难，可利用扩展欧几里得算法（Extended Euclidean algorithm）。

Q：已知 $e$ 和 $n$ 的前提下，计算 $d$ 困难吗？
A：是的，否则RSA将不具有安全性。

至此，我们说明了RSA的正确性。

RSA的安全性

给定 $e$ 和 $n$ 的条件下，很难找到 $d$ 的值
对于攻击者来说，在知道 $p$ 和 $q$ 的前提下，很容易计算出 $n = pq$，而 $n$ 的因子 $d = e^{-1} \bmod \varphi(n)$，其中 $\varphi(n) = \varphi(p)\varphi(q) = (p-1)(q-1)$

所以我们的安全性主要依靠以下两条原则：

表明所有破解 RSA 的方法都可以轻松地因数分解 $n$
证明对大数因数分解是困难的

通过 $\varphi(n)$ 计算 $p$ 和 $q$ 比对 $n$ 直接进行因数分解更容易吗？

\[\varphi(n) = (p-1)(q-1) = pq - (p + q) + 1 = n - (p + q) + 1 \\ p + q = n - \varphi(n) + 1 \]

我们的目标是证明在知道 $\varphi(n)$ 的前提下，我们可以很容易找到 $p$ 和 $q$

\[(p - q)^2 = p^2 -2pq + q^2 = (p + q)^2 - 4pq \\ p - q = \sqrt{(p+q)^2-4n} = \sqrt{(n-\varphi(n)+1)^2-4n} \]

则联立方程组：

\[\begin{cases} p+q=n - \varphi(n) + 1 \\ p-q=\sqrt{(n-\varphi(n)+1)^2-4n} \\ \end{cases} \]

解方程组即可求出 $p$ 与 $q$。所以在知道 $\varphi(n)$ 的前提下，很容易计算出 $p$ 和 $q$。

还需说明目前没有比因数分解 $n$ 更容易的方法计算出 $d$

\[ed = 1 \bmod \varphi(n) \\ k * \varphi(n) = ed - 1 \]

我们已知 $e$（公钥内包含），假设知道一种方法能够轻松地计算出 $d$，则我们很容易得到 $\varphi(n)$，则轻松地完成了对大数 $n$ 的因数分解，很容易破解了RSA。

大数的因数分解有多难？

RSA-129，1994年，1600台机器（129 decimal digits）
RSA-768，2009年，需要2000年的计算（232 digital digits）。这一事件威胁了现通行的1024-bit密钥的安全性，普遍认为用户应尽快升级到2048-bit或以上。
1994年，彼得·秀尔证明一台量子计算机可以在多项式时间内进行因数分解。假如量子计算机有朝一日可以成为一种可行的技术的话，那么秀尔的算法可以淘汰RSA和相关的派生算法。（即依赖于分解大整数困难性的加密算法）

典型密钥长度

NIST建议的RSA密钥长度为至少2048位

已公开的或已知的攻击方法

大数因数分解

针对RSA最流行的攻击一般是基于大数因数分解。1999年，RSA-155（512 bits）被成功分解，花了五个月时间（约8000 MIPS年）和224 CPU hours在一台有3.2G中央内存的Cray C916计算机上完成。

2009年12月12日，编号为RSA-768（768 bits, 232 digits）数也被成功分解。这一事件威胁了现通行的1024-bit密钥的安全性，普遍认为用户应尽快升级到2048-bit或以上。

时间攻击

1995年，丹·博内和大卫·布鲁姆利提出了一种非常意想不到的攻击方式：假如Eve（窃密者）对Alice的硬件有充分的了解，而且知道它对一些特定的消息加密时所需要的时间的话，那么她可以很快地推导出d。这种攻击方式之所以会成立，主要是因为在进行加密时所进行的模指数运算是一个比特一个比特进行的，而比特为1所花的运算比比特为0的运算要多很多，因此若能得到多组信息与其加密时间，就会有机会可以反推出私钥的内容。

利用RSA加密一个文档

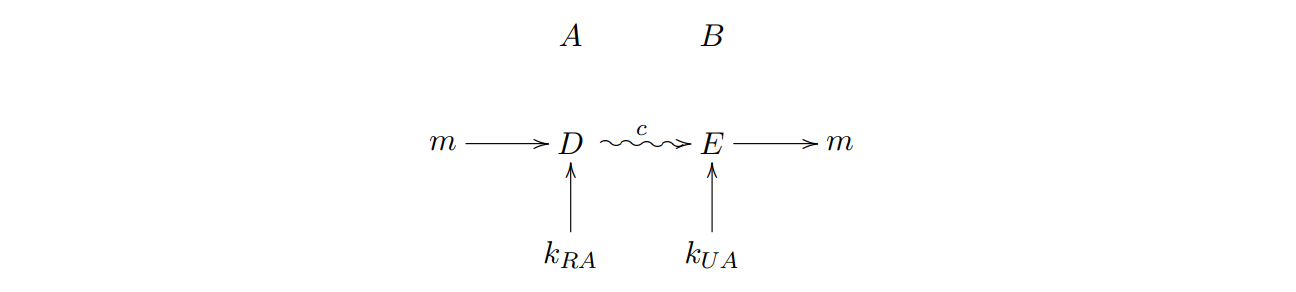
但是，RSA加密算法代价昂贵：加密相同大小的明文，RSA需要花费使用对称加密方法1000倍左右的时间。

那么我们如何利用RSA加密一个大型文档呢？
实际的运用中（如TLS）一般结合了对称加密（如AES）和非对称加密（如RSA）两者
假设我们有公钥 $K_U$ 和私钥 $K_R$ ，加密算法RSA，以及加密哈希函数 $H$

\[<m,RSA_{K_R}(H(m))> \]

利用RSA加密部分摘要，剩余的大部分明文继续采用对称加密方法。

最后，留下一个问题，使用非对称加密算法时，Bob如何获取到Alice的公钥呢？请参看如何构建公钥基础设施PKI

posted @ 2022-11-20 17:44 S!no 阅读(254) 评论(0) 编辑收藏举报

刷新页面返回顶部

S!no