Applied Cryptography（3）——密钥分发（Key Distribution）

密钥分发（Key Distribution）

• 密钥分发（Key Distribution）
  • Solution#0 Pairwise Shared Keys
  • Solution#0B Use a Trusted Third Party
  • Solution#1 Merkle’s Puzzle
  • Diffie-Hellman Key Exchange
    • Secret Paint Mixing(Simon Sigh, The Code Book)
    • DHKE（Diffie-Hellman Key Exchange）

在对称密码中，所有参与方都使用相同的密钥进行加密和解密。密钥可以相同，或者两个密钥之间可以进行简单的转换。对称密码的重要属性是利用相同的密钥进行加密和解密。如果 2 方或更多方想要相互交谈，他们首先必须就密钥达成一致。这意味着各方必须有一种方法可以在不暴露密钥的情况下传达该密钥。早些时候，这是通过密码本（根据物理特性分发）完成的，这是不切实际的。 现在有不同的方法来建立安全密钥。

Solution#0 Pairwise Shared Keys

每两位参与者之间都有成对的共享密钥

Solution#0B Use a Trusted Third Party

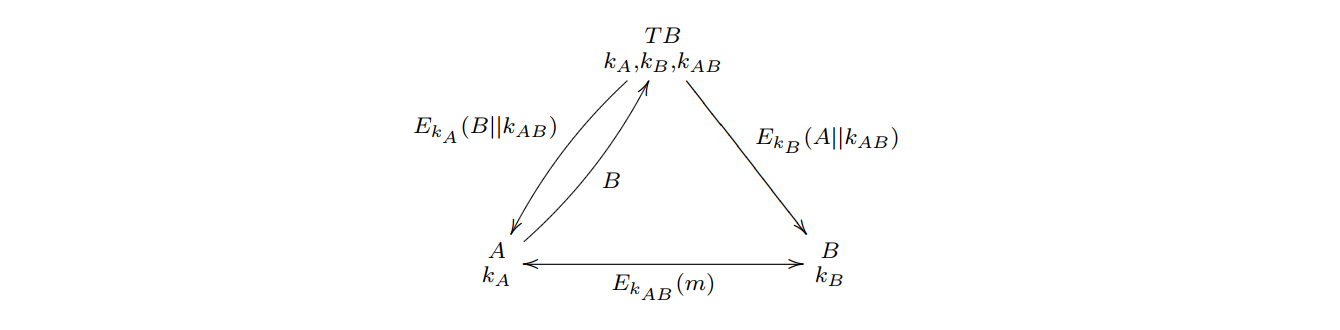
缺点：

1. 第三方可以获取到A与B之间的所有消息
2. 第三方可以冒充任意一位参与方
3. 攻击者可能会通过加解密方法获取密钥

Solution#1 Merkle’s Puzzle

The Merkle’s Puzzle was the first key exchange protocol, without the parties sharing a secret
key with another or third party (trusted place).

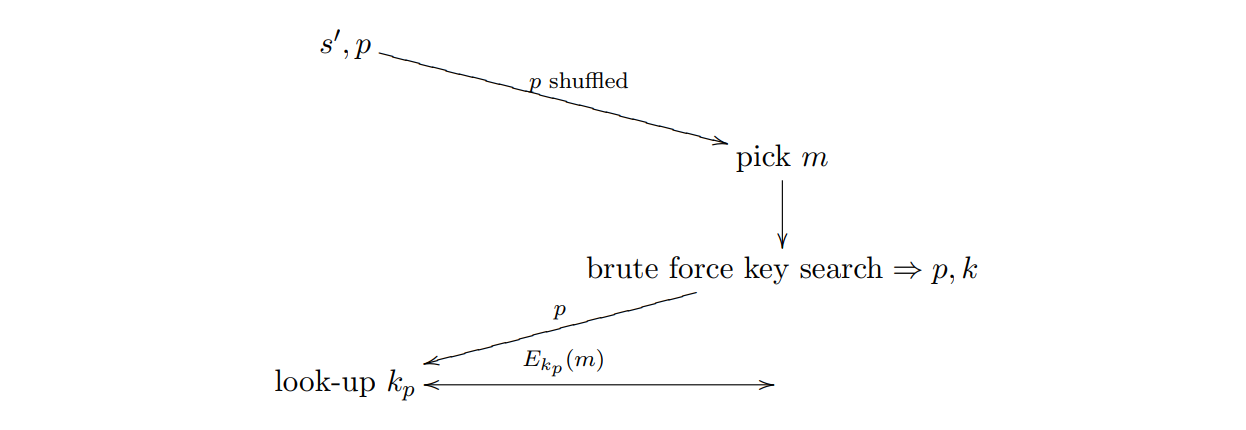
The Merkle’s Puzzle is an impractical idea as it requires a lot of secrets and puzzles to create
for A and a good bandwith to send this information to B so that an attacker can’t get the key too easy

Diffie-Hellman Key Exchange

密码学史上的重要事件

• 1949，Shannon(香农)发表论文《保密系统的通信原理》
  • 意义：密码学的理论基础之一，发表30年后才显示出它的价值
• 1976，Diffie,Hellman发表论文《密码学的新方向》
  • 意义：开辟了公钥密码学的新领域，可以说，没有公钥密码的研究就没有现代密码学
• 1977，RSA密码体制出现
  • 意义：公钥密码领域最杰出的代表，事实上的标准，密码学史上的里程碑
• 1978，DES（数据加密标准）出现
  • 意义：美国的数据加密标准，用于政府等非机密单位及商业的保密通信

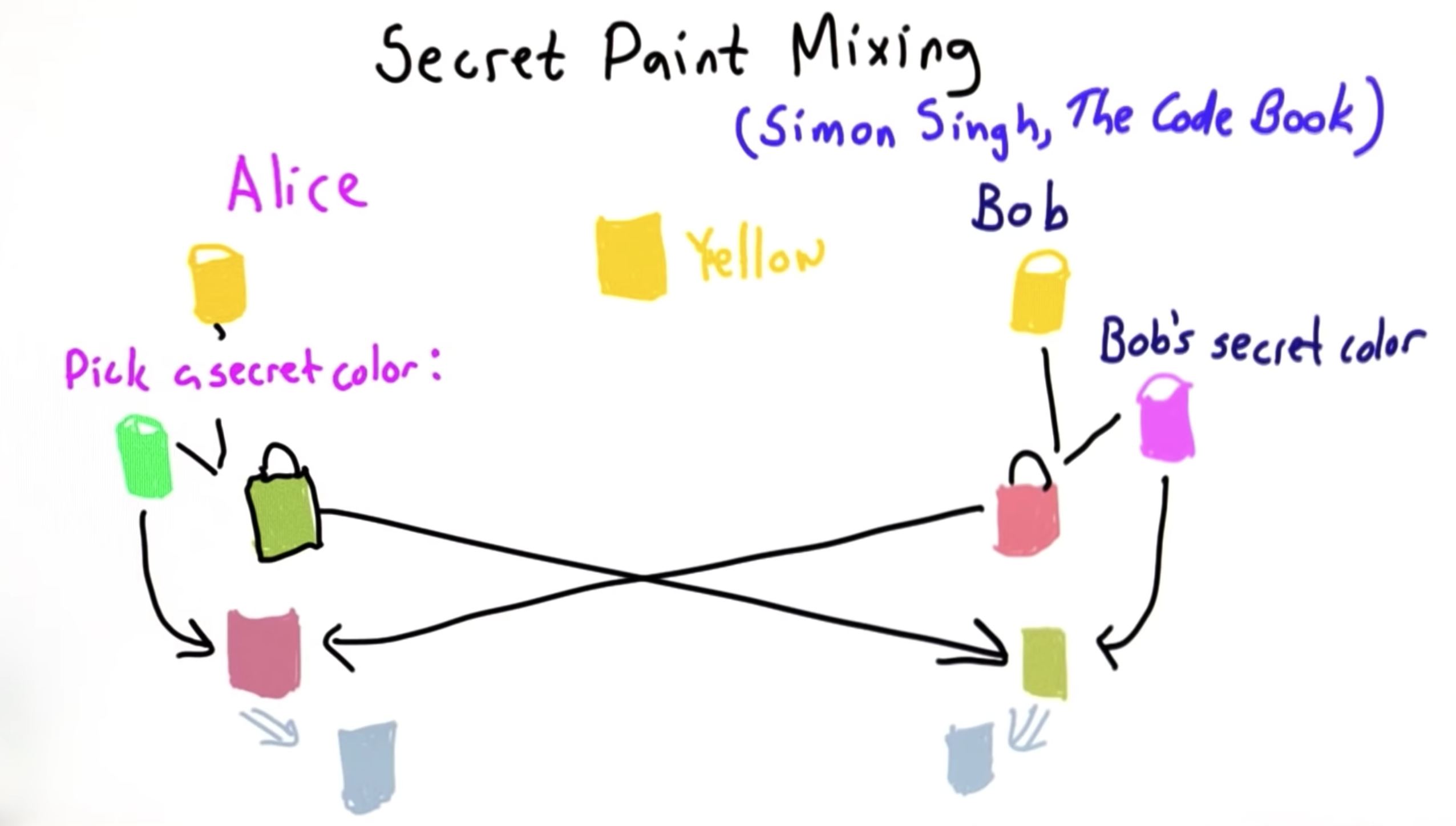
Secret Paint Mixing(Simon Sigh, The Code Book)

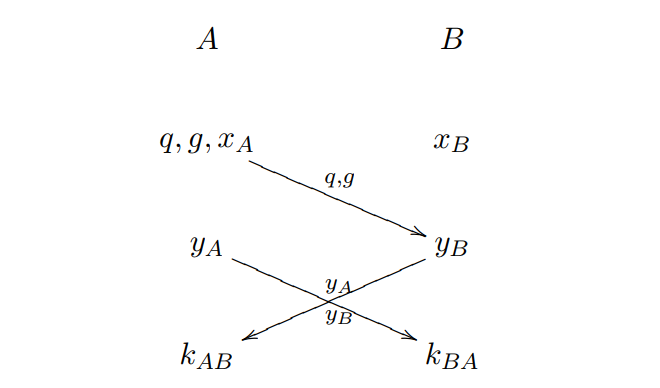
DHKE（Diffie-Hellman Key Exchange）

乘法性质：

$$ab = ba$$

$$(a^b)^c = a^{bc} = a^{cb} = (a^c)^b$$

$q$ 是一个大质数，$g$ 是 $q$ 的原根（primitive root）
原根定义：

$$x \in [1, q-1], \exists k, g^k = x$$

D-H加密流程：

1. Alice选择一个秘密整数 $a$，计算 $y_A = g^a \bmod q$，并发送给Bob
2. Bob选择一个秘密整数 $b$，计算 $y_B = g^b \bmod q$，并发送给Alice
3. Alice计算 $k_{AB} = y_B^a \bmod q = g^{ab} \bmod q$
4. Bob计算 $k_{AB} = y_A^b \bmod q = g^{ab} \bmod q$

至此，双方秘密获得了相同的密钥 $k_{AB}$

基于离散对数问题(discrete logarithm problem)，已知 $y_A, y_B, g, q$ 的前提下，破解该加密方式是不可行的

$$a^x = b \bmod n$$

$$x = d \log_a b$$

难以解出 $x$

如果 $q$ 是一个至少 300 位的质数，并且 $a$ 和 $b$ 至少有100位长，那么即使使用全人类所有的计算资源和当今最好的算法也不可能从 $g, q$ 和 $g^a \bmod q$ 中计算出 $a$。这个问题就是著名的离散对数问题