Applied Cryptography(2)——对称密码的应用(Application of Symmetric Ciphers)
对称密码的应用(Application of Symmetric Ciphers)
- 对称密码的应用(Application of Symmetric Ciphers)
一、生成随机密钥(Generating Random Keys)
-
柯尔莫哥洛夫随机性(Kolomogorov Randomness):一个字符串是随机的当且仅当它的长度小于任意能够输出这个字符串的计算机程序的长度
-
柯尔莫哥洛夫复杂度(Kolomogorov Complexity):一个字符串s的柯氏复杂度是能够输出且仅输出这个字符串的最短计算机程序的长度
-
定理:柯氏复杂度不可计算
-
证明思路:培里悖论(The Berrry Paradoxon)
- ’What is the smallest natural number that cannot be described in eleven words?’
- 不能用少于19个字命名的最小整数
二、随机数生成器(Pseudo Random Number Generator,PRNG)
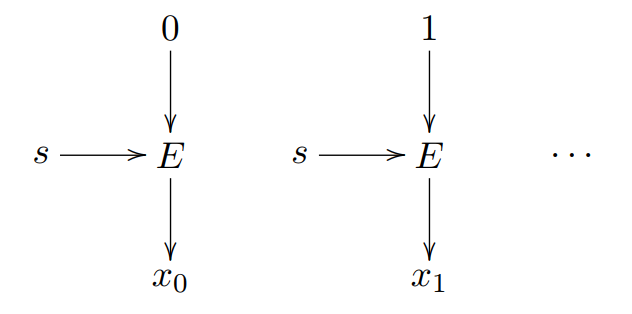
三、分组密码的五种工作模式(Modes of Operation)
密码学中,分组密码的工作模式(mode of operation)允许使用同一个分组密码密钥对多于一块的数据进行加密,并保证其安全性。分组密码自身只能加密长度等于密码分组长度的单块数据,若要加密变长数据,则数据必须先被划分为一些单独的密码块。通常而言,最后一块数据也需要使用合适填充方式将数据扩展到符合密码块大小的长度。一种工作模式描述了加密每一数据块的过程,并常常使用基于一个通常称为初始化向量的附加输入值以进行随机化,以保证安全。
3.1 电子密码本(Electronic Codebook Mode,ECB)
最简单的加密模式即为电子密码本模式。需要加密的消息按照块密码的块大小被分为数个块,并对每个块进行独立加密。
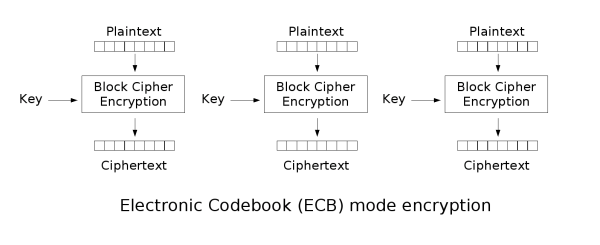
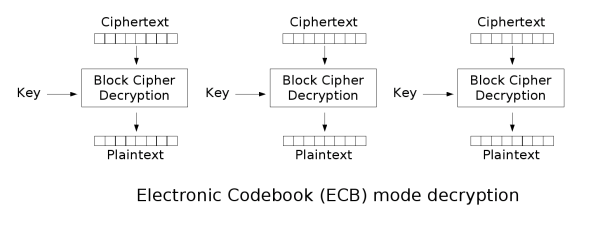
本方法主要有两个缺点:
- 一是在于同样的明文块会被加密成相同的密文块;因此,它不能很好的隐藏数据模式。
- 二是攻击者能够任意移动调换密文块的位置,导致解码后的明文顺序混乱。
3.2 密码块连接(Cipher Block Chaining Mode,CBC)
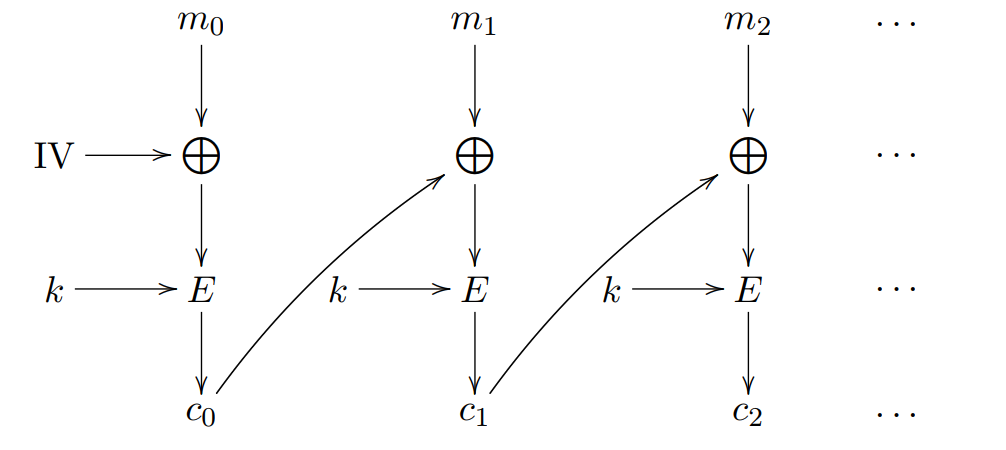
在CBC模式中,每个明文块先与前一个密文块进行异或后,再进行加密。在这种方法中,每个密文块都依赖于它前面的所有明文块。同时,为了保证每条消息的唯一性,在第一个块中需要使用初始化向量。
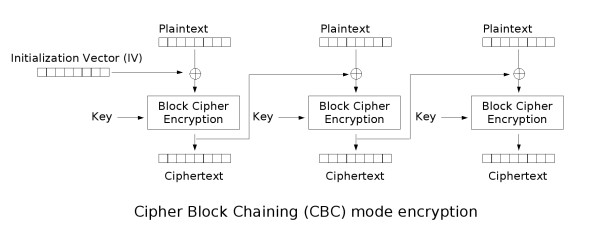
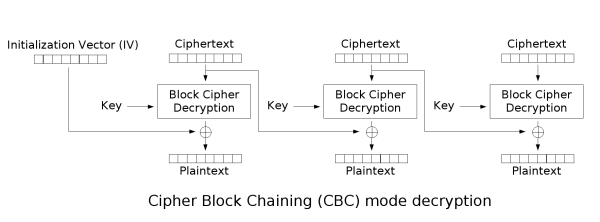
CBC是最为常用的工作模式。它的主要缺点在于加密过程是串行的,无法被并行化,而且消息必须被填充到块大小的整数倍。解决后一个问题的一种方法是利用密文窃取。
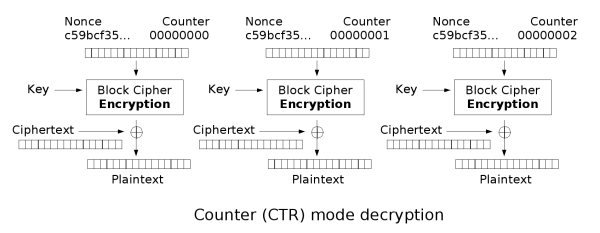
3.3 计数器模式(Counter Mode,CTR)
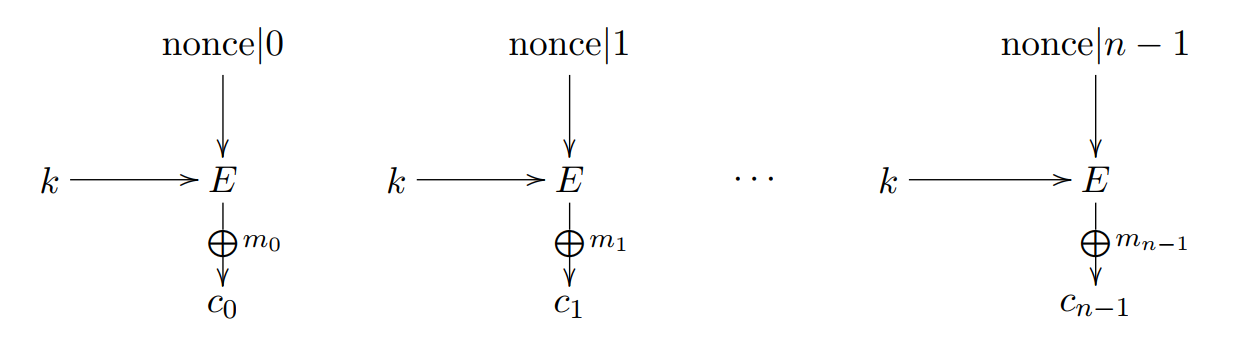
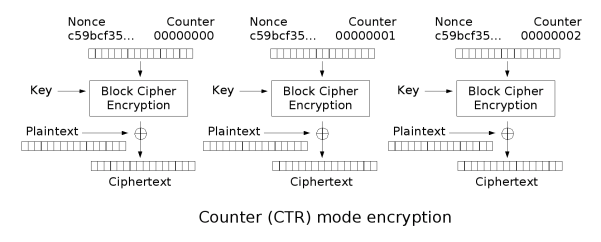
CTR将块密码变为流密码。它通过递增一个加密计数器以产生连续的密钥流,其中,计数器可以是任意保证长时间不产生重复输出的函数,但使用一个普通的计数器是最简单和最常见的做法。
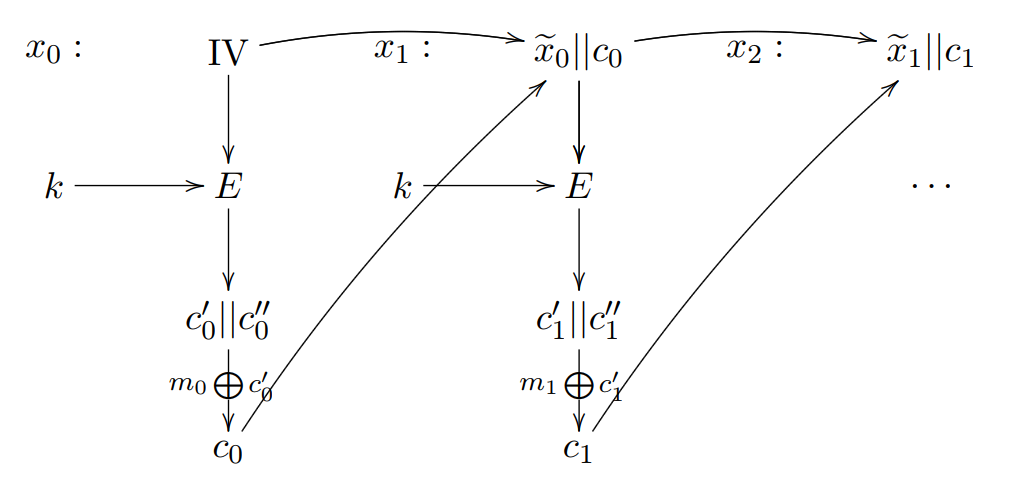
3.4 密文反馈模式(CFB,Cipher Feedback Mode)
密文反馈模式类似于CBC,可以将块密码变为自同步的流密码;工作过程亦非常相似,CFB的解密过程几乎就是颠倒的CBC的加密过程。
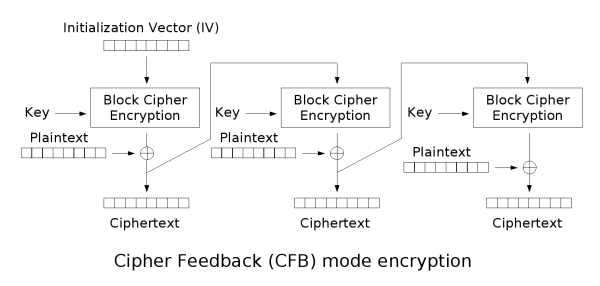
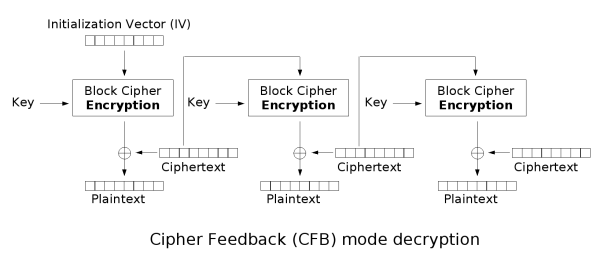
与CBC相似,明文的改变会影响接下来所有的密文,因此加密过程不能并行化;而同样的,与CBC类似,解密过程是可以并行化的。在解密时,密文中一位数据的改变仅会影响两个明文块:对应明文块中的一位数据与下一块中全部的数据,而之后的数据将恢复正常。
CFB拥有一些CBC所不具备的特性,这些特性与OFB和CTR的流模式相似:只需要使用块密码进行加密操作,且消息无需进行填充(虽然密文窃取也允许数据不进行填充)。
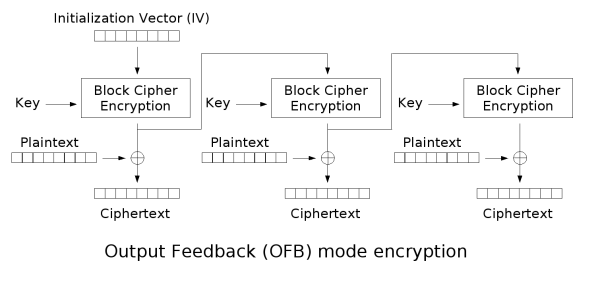
3.5 输出反馈模式(Output feedback, OFB)
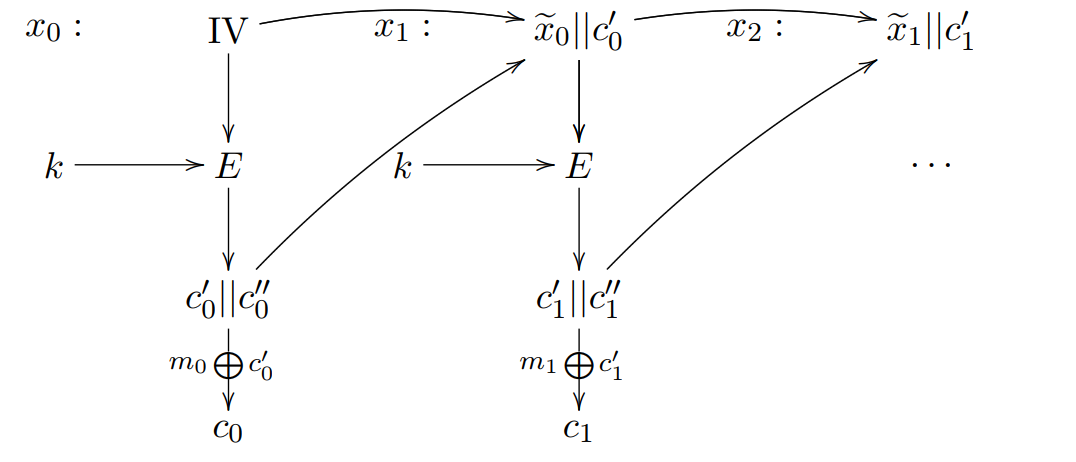
输出反馈模式可以将块密码变成同步的流密码。它产生密钥流的块,然后将其与明文块进行异或,得到密文。与其它流密码一样,密文中一个位的翻转会使明文中同样位置的位也产生翻转。这种特性使得许多错误校正码,例如奇偶校验位,即使在加密前计算,而在加密后进行校验也可以得出正确结果。
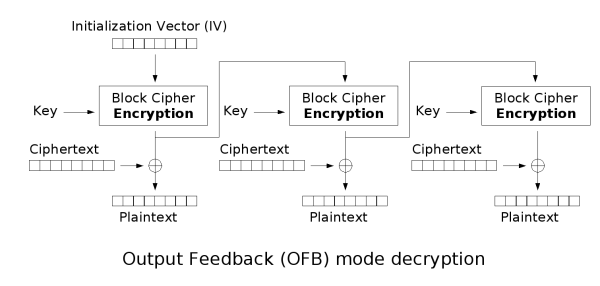
由于XOR操作的对称性,加密和解密操作是完全相同的。
四、填充(Padding)
块密码只能对确定长度的数据块进行处理,而消息的长度通常是可变的。因此部分模式(即ECB和CBC)需要最后一块在加密前进行填充。有数种填充方法,其中最简单的一种是在明文的最后填充空字符以使其长度为块长度的整数倍,但必须保证可以恢复明文的原始长度
CFB,OFB和CTR模式不需要对长度不为密码块大小整数倍的消息进行特别的处理。因为这些模式是通过对块密码的输出与明文进行异或工作的。最后一个明文块(可能是不完整的)与密钥流块的前几个字节异或后,产生了与该明文块大小相同的密文块。流密码的这个特性使得它们可以应用在需要密文和明文数据长度严格相等的场合,也可以应用在以流形式传输数据而不便于进行填充的场合。
五、密码散列函数
密码散列函数是一种单向函数,也就是说极其难以由散列函数输出的结果,回推输入的资料是什么。这样的单向函数被称为“现代密码学的驮马”。这种散列函数的输入资料,通常被称为消息(message),而它的输出结果,经常被称为消息摘要(message digest)或摘要(digest)。
常规哈希函数具有的性质(Regular Hash Function):
- 压缩性(Compression):散列函数较大的输入生成固定较小的输出
- 分布(Distribution):
密码散列函数具有的性质(Cryptographic Hash Function):
- 对于任何一个给定的消息,它都很容易就能运算出散列数值
- 原相抗性(Pre-image resistance :"one-way-ness"): Given then it’s hard to solve for for
- 难以由一个已知的散列数值,去推算出原始的消息
- Weak collision resistance (second pre-image resistance): given an input and a hashing function , it is very difficult to find another input on which
- 在不改动散列数值的前提下,修改消息内容是不可行的
- Strong collision resistance(collision resistance): given a hashing function and two arbitrary inputs and , there exists an absolute minimum chance of being equal to
- 对于两个不同的消息,只有极低的几率会产生相同的散列数值
六、随机预言机(Random Oracle)
随机预言机是一部预言机(简单说像是理论的黑箱),对任何输入都回传一个真正均匀随机的输出(参考离散型均匀分布),不过对相同的输入,该预言机每次都会用同一方法输出。换句话说,随机预言机是一个将所有可能输入与输出作随机映射的函数。
Theorem: It is impossible to construct a random oracle.
七、加盐的密码模式(Salted password scheme)
盐(Salt),在密码学中,是指在散列之前将散列内容(例如:密码)的任意固定位置插入特定的字符串。这个在散列中加入字符串的方式称为“加盐”。其作用是让加盐后的散列结果和没有加盐的结果不相同,在不同的应用情景中,这个处理可以增加额外的安全性。
在大部分情况,盐是不需要保密的。盐可以是随机产生的字符串,其插入的位置可以也是随意而定。如果这个散列结果在将来需要进行验证(例如:验证用户输入的密码),则需要将已使用的盐记录下来。
八、哈希链(Hash Chain)
Avoid password reuse.
哈希链 是将密码学中的哈希函数循环地用于一个字符串。(即将所得哈希值再次传递给哈希函数得至其哈希值)
例:
一个长度为4哈希链,通常记



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】