8.1 考试总结
考试背景：
放假18个小时后，回到学校，随即迎来8月第一场考试，考试时间从下午一点五十到五点十分，但可能由于刚放了假，同学们身心疲倦（逻辑上似乎说不通。。），都来的有些晚，考试时间推迟了五分钟。天气很热，机房里空调开到十七度，吹出阵阵白气，山大附中的同学没有来，机房里非常安静，只有零零星星敲击键盘的声音（其中有我敲快读的声音，可能会被旁边那位大佬打一顿。。）。
考试过程：
开始考试后，阅读题目，惊奇的发现，第一题近乎原题，但心里有些发虚，因为那道原题是我用桶排序水过的，正解是线段树二分建树统计贡献，然而我并没有打，于是两分钟先码了一个暴力，拿到了40分，去看下面的题，于是乎，我进入了深深的绝望。。发现除了暴力dfs，我一点思路都没有，于是又回到第一题，硬着头皮打我并不是特别熟悉的线段树，果不其然，一颗线段树，硬生生调了一个半小时。。不过，最后还是调对了，T1最终得分90，T了一个点，后来经多方考察，发现用一个精（du）妙（liu）的技巧——循环展开，可以迅速A掉，hzoi-cbx大佬更是用暴力，跑出我正解七分之一的时间。。码完第一题，我浑身是汗（调不出来急得。。），脱下了校服，开始打下面的题，我旁边那位大佬却冷得缩成了一团。。并没有理他，继续我的骗分之路。T2的思路，那是一点也没有。。打了个暴搜瞬间过样例，于是手模了一个大点，跑了20分钟。。于是乎，T2最终得分20，和期望得分一样，这实际上是一道神DP，旁边那位成为全场唯一一个AC的%%%%%%%%%。T3实际上也差不多，由于我的位运算掌握的不好，并没有看出所给式子的实际含义，于是只能码一个暴力模拟，加上一些卡常技巧，本以为能拿到40分，结果却只有30分，尴尬至极。全都码完后，考试还剩半个多小时，反反复复检查了好几遍，给T1优化了一下码风，T2加了一个剪枝，T3。。没啥变化。。考试结束，最终得分90+20+30=140分，rank 3/52，rank1是外校的国赛铜牌选手，跟我们一个年级，拿到了200分，深感惭愧，rank2当然是旁边的大佬，180分，也是碾压全场，在日后的学习中，要多加借鉴，考出水平，考出素质，考出状态。
考试题解：
T1：
同 [Tjoi2016&Heoi2016]排序 一题，把数串换做字符串，最后一次查询换做全部输出，但这丝毫不影响桶排的O(n)复杂度对于sort O(nlogn) 本身的优越性，加上我对桶排的熟悉度（用它水了好多题。。），于是我决定使用桶排来完成题目的要求，但观察数据范围，发现桶排的复杂度并不足以支撑这个题目，所以我们采用线段树优化桶排的方式，来使我们的期望复杂度尽可能低。复杂度O(mlogn*26)，m为操作数，每次区间修改logn，修改26次。由于线段树自身的大常数，我们需要用一些卡常技巧（循环展开）来优化我们26倍的常数。
那么整体思路是，线段树动态维护每一个区间内，a-z各自出现的个数，利用区间覆盖，来修改区间排序后的值，利用懒标记下传，来维护整个序列的整体性，与赋值的正确性，利用桶排思想进行区间覆盖。
例如一串字母 ababcd ，其中 a出现2次，tr[x].a[a]=2，同理，tr[x].a[b]=2，tr[x].a[c]=1，tr[x].a[d]=1;那么我们按序输出，也就是按序覆盖，得到区间为aabbcd，完成了一次区间覆盖操作，具体操作是要将操作区间所对应的线段树序列上的节点信息合并为一个桶，递归统计答案。
其中懒标记维护的是一个区间内，出现的都是同一个字母的个数，所以是以懒标记为下标，维护一段区间长度即可。
最后统计答案时可以深搜遍历一边线段树，将节点信息合并，完成答案统计。
代码如下：
#include<bits/stdc++.h> #define re register using namespace std; int n,m,ans[30],tot=0; char s[200010]; struct node{int l,r,lz,a[30];}tr[800010]; inline int read(){ re int a=0,b=1; re char ch=getchar(); while(ch<'0'||ch>'9') b=(ch=='-')?-1:1,ch=getchar(); while(ch>='0'&&ch<='9') a=(a<<3)+(a<<1)+(ch^48),ch=getchar(); return a*b; } inline void pushdown(re int x){ if(tr[x].lz){ tr[x<<1].a[1]=tr[x<<1].a[2]=tr[x<<1].a[3]=tr[x<<1].a[4]=tr[x<<1].a[5]=tr[x<<1].a[6]=tr[x<<1].a[7]=tr[x<<1].a[8]=tr[x<<1].a[9]=tr[x<<1].a[10]= tr[x<<1].a[11]=tr[x<<1].a[12]=tr[x<<1].a[13]=tr[x<<1].a[14]=tr[x<<1].a[15]=tr[x<<1].a[16]=tr[x<<1].a[17]=tr[x<<1].a[18]=tr[x<<1].a[19]= tr[x<<1].a[20]=tr[x<<1].a[21]=tr[x<<1].a[22]=tr[x<<1].a[23]=tr[x<<1].a[24]=tr[x<<1].a[25]=tr[x<<1].a[26]=tr[x<<1|1].a[1]=tr[x<<1|1].a[2]= tr[x<<1|1].a[3]=tr[x<<1|1].a[4]=tr[x<<1|1].a[5]=tr[x<<1|1].a[6]=tr[x<<1|1].a[7]=tr[x<<1|1].a[8]=tr[x<<1|1].a[9]=tr[x<<1|1].a[10]= tr[x<<1|1].a[11]=tr[x<<1|1].a[12]=tr[x<<1|1].a[13]=tr[x<<1|1].a[14]=tr[x<<1|1].a[15]=tr[x<<1|1].a[16]=tr[x<<1|1].a[17]=tr[x<<1|1].a[18]=tr[x<<1|1].a[19]= tr[x<<1|1].a[20]=tr[x<<1|1].a[21]=tr[x<<1|1].a[22]=tr[x<<1|1].a[23]=tr[x<<1|1].a[24]=tr[x<<1|1].a[25]=tr[x<<1|1].a[26]=0; re int lazy=tr[x].lz; tr[x].lz=0; tr[x<<1].a[lazy]=tr[x<<1].r-tr[x<<1].l+1; tr[x<<1|1].a[lazy]=tr[x<<1|1].r-tr[x<<1|1].l+1; tr[x<<1].lz=tr[x<<1|1].lz=lazy; } } inline void pushup(re int x){ for(re int i=1;i<=26;i++) tr[x].a[i]=tr[x<<1].a[i]+tr[x<<1|1].a[i]; } inline void build(re int x,re int l,re int r){ tr[x].l=l;tr[x].r=r;tr[x].lz=0; if(l==r){tr[x].a[s[l]-'a'+1]=1;return;} re int mid=(l+r)>>1; build(x<<1,l,mid),build(x<<1|1,mid+1,r); pushup(x); } inline void query(re int x,re int l,re int r){ if(tr[x].l>=l&&tr[x].r<=r){ for(re int i=1;i<=26;i++) ans[i]+=tr[x].a[i]; return ; } pushdown(x); re int mid=(tr[x].l+tr[x].r)>>1; if(l<=mid) query(x<<1,l,r); if(r>mid) query(x<<1|1,l,r); } inline void change(re int x,re int l,re int r,re int k){ if(tr[x].l>=l&&tr[x].r<=r){ tr[x].a[1]=tr[x].a[2]=tr[x].a[3]=tr[x].a[4]=tr[x].a[5]=tr[x].a[6]=tr[x].a[7]=tr[x].a[8]=tr[x].a[9]=tr[x].a[10]= tr[x].a[11]=tr[x].a[12]=tr[x].a[13]=tr[x].a[14]=tr[x].a[15]=tr[x].a[16]=tr[x].a[17]=tr[x].a[18]=tr[x].a[19]= tr[x].a[20]=tr[x].a[21]=tr[x].a[22]=tr[x].a[23]=tr[x].a[24]=tr[x].a[25]=tr[x].a[26]=0; tr[x].a[k]=tr[x].r-tr[x].l+1; tr[x].lz=k; return ; } pushdown(x); re int mid=(tr[x].l+tr[x].r)>>1; if(l<=mid) change(x<<1,l,r,k); if(r>mid) change(x<<1|1,l,r,k); pushup(x); } inline void search(re int x) { if(tr[x].l==tr[x].r) for(re int i=1;i<=26;i++) if(tr[x].a[i]){s[++tot]=i+'a'-1;return;} pushdown(x); search(x<<1); search(x<<1|1); } signed main(){ n=read(),m=read(); scanf("%s",s+1); build(1,1,n); while(m--){ re int l=read(),r=read(),x=read(); ans[1]=ans[2]=ans[3]=ans[4]=ans[5]=ans[6]=ans[7]=ans[8]=ans[9]=ans[10]= ans[11]=ans[12]=ans[13]=ans[14]=ans[15]=ans[16]=ans[17]=ans[18]=ans[19]= ans[20]=ans[21]=ans[22]=ans[23]=ans[24]=ans[25]=ans[26]=0; query(1,l,r); if(x==1){ for(re int i=1;i<=26;i++) if(ans[i]){ change(1,l,l+ans[i]-1,i); l+=ans[i]; } continue; } if(x==0){ for(re int i=26;i;i--) if(ans[i]){ change(1,l,l+ans[i]-1,i); l+=ans[i]; } continue; } } search(1); printf("%s",s+1); return 0; }
T2：
可以利用奇袭一题的思路思考，将一个矩阵，拍做一列，发现一定恰好有n个点，遍布抽象序列，于是可以使用dp横向转移，真的是神思路。
设l[i]为到i列时结束了的左区间的个数，r[i]到i列开始的右区间个数
思路一：
1.有j个1放在右区间，那么也就有i-j放在了左区间。又因为在这一列之前结束的左区间在之前已经放上，所以就剩了i-j-l[i-1]个1，可以放在在第i列结束的左区间里，当然这些个1可以放在之前某一列里，那么对答案的贡献就要乘上A(i-j-l[i-1],l[i]-l[i-1])了。
2.到i列时不放新的1，f[i][j]=f[i-1][j];如果放了一个：f[i][j+1]+=f[i-1][j]*(r[i]-j)；解释一下，新放的那个1，能放在i列已开始的右区间里，但要去掉已经放了的j个区间。
思路二：
我们发现题目除了对哪一行的一个区间内的1的个数有要求外，主要的大前提是每列不能出现多于1个的1，所以我们发现，其实主要是对列有要求，所以dp思路是对列进行。我们枚举每一列，对右边排了几个1进行一一地枚举，然后算出方案数，再对左边枚举，再算出方案数，（记得取%）
如此转移即可，但注意，1转移一定要在2转移完成后再进行，保证不会有区间重复运算。
以下为思路二的实现：
#include<bits/stdc++.h> #define re register #define mod 998244353 #define int long long using namespace std; int n,m,sl[3001],sr[3001],f[3001][3001]; signed main(){ scanf("%lld%lld",&n,&m);f[0][0]=1; for(re int i=1,l,r;i<=n;i++) scanf("%lld%lld",&l,&r),++sl[l],++sr[r]; for(re int i=2;i<=m;i++) sl[i]+=sl[i-1],sr[i]+=sr[i-1]; for(re int i=1;i<=m;i++){ f[i][0]=f[i-1][0]; for(re int j=1;j<=i;j++) (f[i][j]=f[i-1][j-1]*(sr[i]-j+1)%mod+f[i-1][j])%=mod; for(re int j=sl[i-1];j<sl[i];j++) for(re int k=0;k<i;k++) (f[i][k]*=(i-k-j))%=mod; } printf("%lld\n",f[m][n]%mod); return 0; }
T3:
此题运用了01trie树的思路，01字典树主要用于解决求异或最值的问题。
01字典树和普通的字典树原理类似，只不过把插入字符改成了插入二进制串的每一位（0或1）。
1 int tol; //节点个数 2 LL val[32*MAXN]; //点的值 3 int ch[32*MAXN][2]; //边的值 4 void init() 5 { //初始化 6 tol=1; 7 ch[0][0]=ch[0][1]=0; 8 } 9 void insert(LL x) 10 { //往 01字典树中插入 x 11 int u=0; 12 for(int i=32;i>=0;i--) 13 { 14 int v=(x>>i)&1; 15 if(!ch[u][v]) 16 { //如果节点未被访问过 17 ch[tol][0]=ch[tol][1]=0; //将当前节点的边值初始化 18 val[tol]=0; //节点值为0，表示到此不是一个数 19 ch[u][v]=tol++; //边指向的节点编号 20 } 21 u=ch[u][v]; //下一节点 22 } 23 val[u]=x; //节点值为 x，即到此是一个数 24 } 25 LL query(LL x) 26 { //查询所有数中和 x异或结果最大的数 27 int u=0; 28 for(int i=32;i>=0;i--) 29 { 30 int v=(x>>i)&1; 31 //利用贪心策略，优先寻找和当前位不同的数 32 if(ch[u][v^1]) u=ch[u][v^1]; 33 else u=ch[u][v]; 34 } 35 return val[u]; //返回结果 36 }
1. 01字典树是一棵最多 32层的二叉树，其每个节点的两条边分别表示二进制的某一位的值为 0 还是为 1. 将某个路径上边的值连起来就得到一个二进制串。
2.节点个数为 1 的层（最高层）节点的边对应着二进制串的最高位。
3.以上代码中，ch[i] 表示一个节点，ch[i][0] 和 ch[i][1] 表示节点的两条边指向的节点，val[i] 表示节点的值。
4.每个节点主要有 4个属性：节点值、节点编号、两条边指向的下一节点的编号。
5.节点值 val为 0时表示到当前节点为止不能形成一个数，否则 val[i]=数值。
6.可通过贪心的策略来寻找与 x异或结果最大的数，即优先找和 x二进制的未处理的最高位值不同的边对应的点，这样保证结果最大。
对于此题我们发现，最多有2^30种不同的初始值。但是，对于确定的m+1种结果，我们可以确定每一位异或0还是1使得结果最大，而且对手会根据我选的更改答案。观察式子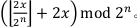
对手做的是将 x 在二进制下左移一位。假设在异或 i 个数后左移,等价于开始时先左移,然后把前 i 个数左移一位。问题转化为选一个数,使它左移一位后,与 m+1 个给定数分别异或的最小值最大。将 m+1 个数建立一棵字典树,从上到下遍历来最大化结果:走到一个点时,如果往下只有 0,说明我们这一位取 1异或后只能是 1,累计结果中加上这一位的值,只有 1 也一样;如果既有 0 又有 1,说明这一位无论怎么取最后都是 0,分别往下走即可。时间复杂度 O(nm)。
#include<bits/stdc++.h> #define re register #define ll long long using namespace std; ll n,m,lim,sum[1000010],a[1000010],cnt,dat[1000010]; ll t[1000010],ch[3000010][2],id ,tot=0,ans[1000010]; inline int read(){ re int a=0,b=1; re char ch=getchar(); while(ch<'0'||ch>'9') b=(ch=='-')?-1:1,ch=getchar(); while(ch>='0'&&ch<='9') a=(a<<3)+(a<<1)+(ch^48),ch=getchar(); return a*b; } inline ll calc(re ll x){ return ((x<<1)/lim+(x<<1))%lim; } inline void insert(re ll x){ for(re int i=0;i<n;i++) t[i]=((x>>(n-i-1))&1); re int u=0; for(re int i=0;i<n;i++){ if(!ch[u][t[i]]) ch[u][t[i]]=++id; u=ch[u][t[i]]; } } inline void dfs(re ll x,re ll now,re ll k){ if(k<0){ans[++cnt]=now;return;} if(ch[x][0]&&!ch[x][1]) dfs(ch[x][0],now^(1<<k),k-1); if(ch[x][1]&&!ch[x][0]) dfs(ch[x][1],now^(1<<k),k-1); if(ch[x][0]&& ch[x][1]) dfs(ch[x][0],now,k-1),dfs(ch[x][1],now,k-1); } signed main(){ n=read(),m=read();lim=(1<<n); for(re ll i=1;i<=m;i++) a[i]=read(); for(re ll i=m;i>=1;i--) sum[i]=sum[i+1]^a[i]; for(re ll i=0;i<=m;i++){ cnt^=a[i]; dat[i]=calc(cnt)^sum[i+1]; insert(dat[i]); } cnt=0; dfs(0,0,n-1); sort(ans,ans+cnt+1); for(re ll i=cnt;i>=1;i--) if(ans[i]==ans[cnt]) tot++; printf("%lld\n%lld\n", ans[cnt],tot); return 0; }
考试反思：
这场考试中，虽然拿到了rank3，但还有很多不足之处，T2，T3两题都是好题，却一点思路也没有，我还有很大的进步空间，还有很多知识需要去巩固加强，还有很多能力需要去培养加固。模板一定要熟悉，思路一定要清晰，一定要有耐心去码，去调试，不到考试结束，绝不放弃。在时间安排上，也要尽可能趋于合理，学习考试技巧，向他人学习。
