算法题：剑指 Offer 11. 旋转数组的最小数字（题目+思路+代码+注释）时空O(logN) O(1) 0ms击败100%、99.5%用户

方法1提交结果

改进后方法提交结果

题目

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为1。

示例 1：

输入：[3,4,5,1,2]
输出：1
示例 2：

输入：[2,2,2,0,1]
输出：0
注意：本题与主站 154 题相同：https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

• 你不是一开始有序，然后从左边拿了一部分往右边放了，我直接从右边往左走，一旦发现这个数字比左边数字小，那就是他了！
• 提交后时间0ms空间超过97%也还行
• 深入思考，假设长度一亿，从左边只挪了一个去右边，那岂不是按照这个算法要遍历一亿个？
• 因此在此基础上我们需要引入二分查找来搜索这个（比左边小的数）
• 二分法思路改进后的代码 时空复杂度：O(logN) O(1)
  
  当mid大于right证明最小值还在右边区间，那么left = mid +1（因为mid既然比右边的那那么mid一定不是最小值）
  当mid等于right还不能确定，让right往左移一个位置（或者向左移动到不等于之前right的位置）
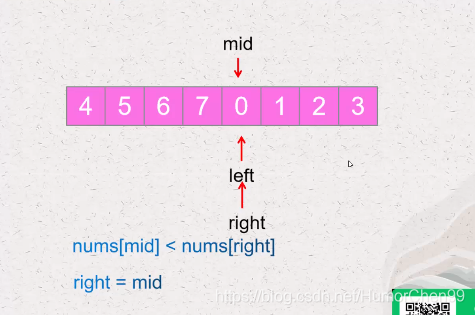
  当mid小于right证明最小值在左边区间，那么right = mid（为什么不减一呢是因为mid这个值有可能就是最小值）;
  不断移动直到最后
  
  按照之前的我们的mid小于right，往左移的时候 right = mid，这个时候我们即可退出循环
  

代码

• 初始版本 时间复杂度最好 O(1) 最坏 O(n) 空间复杂度 O(1) 时间复杂度不太稳定

public int minArray(int[] numbers) {
        for (int i = numbers.length - 1; i > 0; i--) {
            if (numbers[i] < numbers[i - 1]) {
                return numbers[i];
            }
        }
        return numbers[0];
    }

• 改进版本（更稳定，尤其是对于大量数据） 时间复杂度 O(logN) 空间复杂度 O(1)

public int minArray(int[] numbers) {
        int left = 0,right = numbers.length-1,mid;
        while (left < right){
            mid = left + (right-left)/2;
            if (numbers[mid] > numbers[right]){
                left = mid + 1;
            }else if (numbers[mid] == numbers[right]){
                right--;
            }else {
                right = mid;
            }
        }
        return numbers[left];
    }