算法题：42. 接雨水（困难）一次AC 1ms（题目+思路+代码+注释）

题目

42. 接雨水
    给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

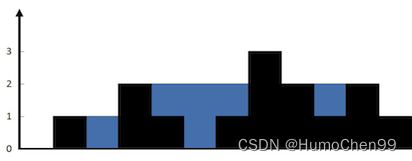
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/trapping-rain-water
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

解题第一步，观察。我们首先要考虑下有没有什么办法能快速计算出，于是我开始思考雨水是怎么盛起来的，于是可知，是从天上掉下来的，那么我们可以在脑海中模拟雨水从最上面往下灌，而能接住多少呢？根据木桶理论，竖着放的木桶能接多少水肯定取决于左右两边最高的木板高度，而在这个二维图中整个能接多少水我们可以拆解为求第i个列最多能接多少水，把每一列能接多少水加起来就是总共能接多少水了！
那么如何求第i个列能接多少雨水呢？首先页面高度取决于左右最高的高度，然后自己列可能也有石块，因此还需要减去自己列石块高度，而自己列石块高度又可能更高，因此需要和0取最大值。
那么这个问题就可以拆分为这么几个问题了
总共能接多少水 = 遍历求第i列能接多少水并求和
第i列能接多少水 = Math.max(Math.min(第i列左边最高的高度,第i列右边最高的高度) - 当前列高度 , 0)

后续优化
由于每次都需要往左边遍历找最左边多高、最右边多高，其实这个是可以提前遍历一次计算好的。

代码

第一版代码先实现，第二版再优化

class Solution {
     public int trap(int[] height) {
        int sum = 0;
        for (int i = 0; i < height.length; i++) {
            sum += pushWater(i, height);
        }
        return sum;
    }


    /**
     * 放水进去
     *
     * @param i
     * @param height
     * @return 返回这个列能装多少水
     */
    int pushWater(int i, int[] height) {
        // 左右两边最高的和减去这个上面的石块,并且必须大于0
        return Math.max(Math.min(getLeftMaxContinueHeight(i, height), getRightMaxContinueHeight(i, height)) - height[i], 0);
    }

    /**
     * 获取左边连续最高的
     *
     * @param i
     * @param height
     * @return
     */
    int getLeftMaxContinueHeight(int i, int[] height) {/*  */
        if (i == 0) {
            return 0;
        }
        int leftMaxHeight = 0, currentHeight = height[i];
        for (int j = i - 1; j >= 0; j--) {
            int leftHeight = height[j];
            if (leftHeight > currentHeight && leftHeight > leftMaxHeight) {
                leftMaxHeight = leftHeight;
            }
        }
        return leftMaxHeight;
    }

    /**
     * 获取右边连续最高的
     *
     * @param i
     * @param height
     * @return
     */
    int getRightMaxContinueHeight(int i, int[] height) {
        if (i == height.length - 1) {
            return 0;
        }
        int rightMaxHeight = 0, currentHeight = height[i];
        for (int j = i + 1; j < height.length; j++) {
            int rightHeight = height[j];
            if (rightHeight > currentHeight && rightHeight > rightMaxHeight) {
                rightMaxHeight = rightHeight;
            }
        }
        return rightMaxHeight;
    }
}

优化后代码 很美妙

这样就计算量非常少了，只需要O（n）时间复杂度即可计算n列的接雨水！

public class Solution {
    @Test
    public void test() {
        int[] ints = {0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
        System.out.println(trap(ints));
//        getLeftMaxContinueHeight(5, ints);
    }

    public int trap(int[] height) {
        // 计算第i项左边最高的高度
        int[] leftMax = new int[height.length];
        leftMax[0] = height[0];
        for (int i = 1; i < height.length; i++) {
            leftMax[i] = leftMax[i - 1];
            if (i - 2 >= 0 && height[i - 1] > leftMax[i]) {
                leftMax[i] = height[i - 1];
            }
        }
        // 第0个左边是0
        leftMax[0] = 0;

        // 计算第i项右边最高的高度
        int[] rightMax = new int[height.length];
        rightMax[height.length - 1] = height[height.length - 1];
        for (int i = height.length - 2; i >= 0; i--) {
            rightMax[i] = rightMax[i + 1];
            if (i + 2 < height.length && height[i + 1] > rightMax[i]) {
                rightMax[i] = height[i + 1];
            }
        }
        // 第0个左边是0
        rightMax[height.length - 1] = 0;

        // 遍历计算第i项雨水个数求和
        int sum = 0;
        for (int i = 0; i < height.length; i++) {
            sum += pushWater(i, height, leftMax[i], rightMax[i]);
        }
        return sum;
    }


    /**
     * 放水进去
     *
     * @param i
     * @param height
     * @return 返回这个列能装多少水
     */
    int pushWater(int i, int[] height, int maxLeft, int maxRight) {
        // 左右两边最高的和减去这个上面的石块,并且必须大于0
        return Math.max(Math.min(maxLeft, maxRight) - height[i], 0);
    }

}