论文笔记1 Learning Common and Specific Features for RGB-D Semantic Segmentation with Deconvolutional Networks
论文发表于ECCV2016
最近一直在做室内语义分割的东西,所以读了这篇文章,之后的实验也准备在这个架构上进行。
Title
Learning Common and Specific Features for RGB-D Semantic Segmentation with Deconvolutional Networks
使用反卷积网络学习rgb-d语义分割的通用和特定特征
Abstract
In this paper, we tackle the problem of RGB-D semantic segmentation of indoor images. We take advantage of deconvolutional networks which can predict pixel-wise class labels, and develop a new structure for deconvolution of multiple modalities. We propose a novel feature transformation network to bridge the convolutional networks and deconvolutional networks. In the feature transformation network, we correlate the two modalities by discovering common features between them, as well as characterize each modality by discovering modality specific features. With the common features, we not only closely correlate the two modalities, but also allow them to borrow features from cach other to enhance the representation of shared information. With specific features, we capture the visual patterns that are only visible in one modality. The proposed network achieves competitive segmentation accuracy on NYU depth dataset V1 and V2.
简而言之,通过反卷积网络,针对RGB与D两种模态的数据分别构建反卷积结构,以及构建为两种数据的共同特征与特定特征所构建的变换层(transformation network)。通过变换层,可以使两种模态的数据相互借鉴增强,提高了真正意义上RGB-D图像的融合处理。
1
简单介绍了室内语义分割的一些问题与难点。

室内物体的无序分布问题,弱光照问题以及遮挡问题。
同时通过一组图例来说明了RGB图像与深度图像在处理过程中各自的关注点所在。
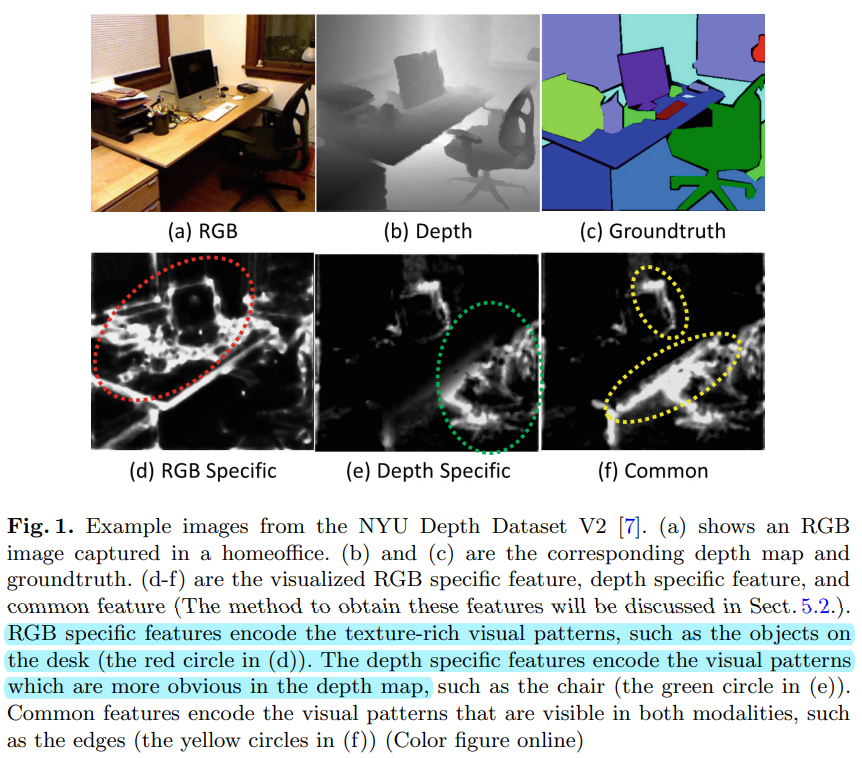
RGB图像在解码中更关注纹理丰富的区域,深度图像更关注深度图像中明显的区域。
2
文章的一个主要核心其实都在讲一件事,就是怎么融合图像和深度的信息,以及如何在融合的基础上,也能提取出图像和深度各自特有的特征以及共有的特征,并被运用到语义分割上。

这里提到了两种数据之间的信息共享,可以增强一定的鲁棒性,解决某些数据获取不全的问题。

需要提取两种数据的共同特征。同时RGB数据更注重外观表达,深度数据更注重深度表达,如何提取两种数据不同的特征。
3
网络架构
这个我也就不细讲,看图就很明白。主要架构也是一个Encoder-decoder,前期的特征提取也是在VGG16的基础上。中间的FC层就是为了提取相似、独自特征,以及融合特征信息交互。
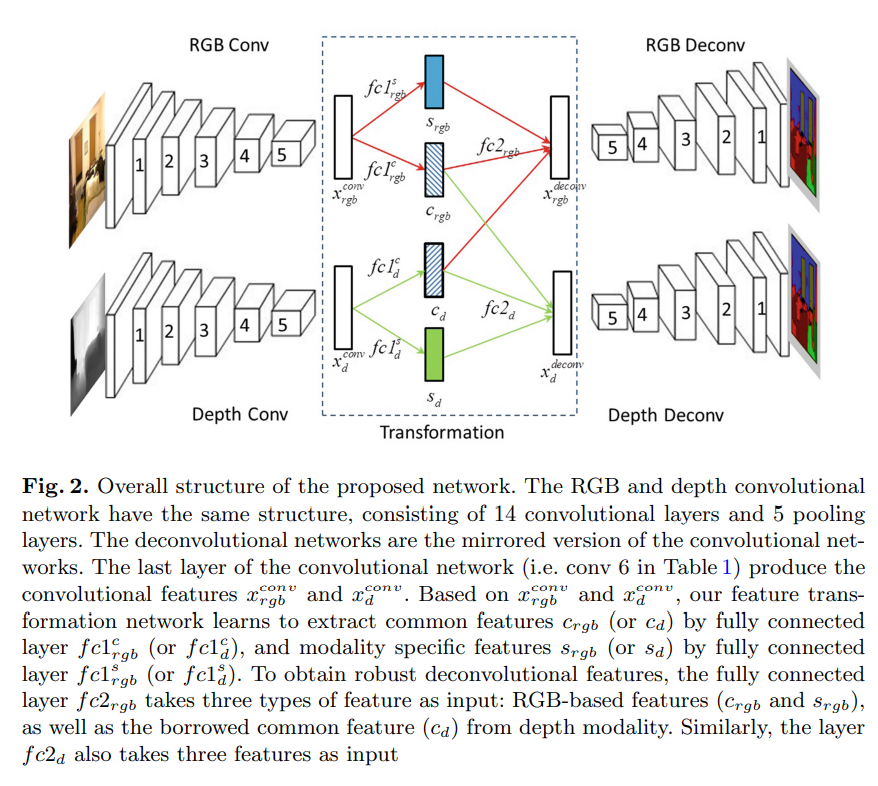
以及卷积核的类型与数量

4
损失函数
这个确实是给了我不少启发。
文章主要使用了MK MMD方法,这个我之后还要接着学习,之后再写吧。这个主要是为了衡量张量之间的距离,以此在变换层中来提取相似特征与独自特征。张量间距离越小,说明越接近相似特征。反之越接近独自特征

其实我当时比较疑惑的就是,有很多方法可以用来判断张量间距离。比如最常用的KL散度、交叉熵、余弦相似度等等,为什么要用MK MMD。文章给出了解释

有许多现有技术可以计算分布之间的相似性,例如熵、互信息或KL散度。然而,这些信息论方法依赖于密度估计,或复杂的空间划分/偏差校正策略,这些策略通常不适用于高维数据。
恍然大悟!


