哈希表(散列表)原理学习
1.定义:
哈希表(Hash table,也叫散列表),是根据关键码值(Key value)而直接进行访问的数据结构。
也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。
这个映射函数叫做散列函数,存放记录的数组叫做散列表。
重要知识点:
1.记录的存储位置=f(关键字)
这里的对应关系f称为散列函数,又称为哈希(Hash函数),
采用散列技术将记录存储在一块连续的存储空间中,
这块连续存储空间称为散列表或哈希表(Hash table)。
2.哈希表的存储方式和查询方式
哈希表hashtable(key,value) 就是把Key通过
一个固定的算法函数既所谓的哈希函数转换成一个整型数字,
然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,
将value存储在以该数字为下标的数组空间里。
(或者:把任意长度的输入(又叫做预映射, pre-image),
通过散列算法,变换成固定长度的输出,该输出就是散列值。
这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,
不同的输入可能会散列成相同的输出,而不可能从散列值来唯一的确定输入值。
简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。)
而当使用哈希表进行查询的时候,就是再次使用哈希函数将key转换为对应的数组下标,
并定位到该空间获取value,如此一来,就可以充分利用到数组的定位性能进行数据定位。
3.哈希表的特点
数组的特点是:寻址容易,插入和删除困难;
而链表的特点是:寻址困难,插入和删除容易。
那么我们能不能综合两者的特性,做出一种寻址容易,插入删除也容易的数据结构?
答案是肯定的,这就是我们要提起的哈希表,哈希表有多种不同的实现方法,
我接下来解释的是最常用的一种方法——拉链法,我们可以理解为“链表的数组”,如图:
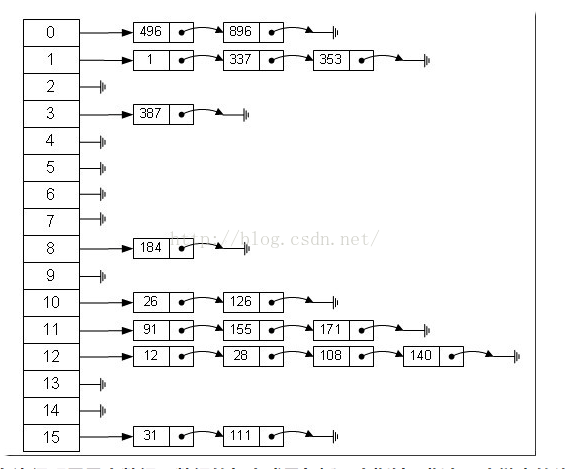
左边很明显是个数组,数组的每个成员包括一个指针,
指向一个链表的头,当然这个链表可能为空,也可能元素很多。
我们根据元素的一些特征把元素分配到不同的链表中去,
也是根据这些特征,找到正确的链表,再从链表中找出这个元素。
2.Hash的应用:
场景一:
Hash主要用于信息安全领域中加密算法,它把一些不同长度的信息转化成杂乱的128位的编码,
这些编码值叫做Hash值. 也可以说,Hash就是找到一种数据内容和数据存放地址之间的映射关系。
场景二:
查找:哈希表,又称为散列,是一种更加快捷的查找技术。
我们之前的查找,都是这样一种思路:集合中拿出来一个元素,
看看是否与我们要找的相等,如果不等,缩小范围,继续查找。
而哈希表是完全另外一种思路:当我知道key值以后,
我就可以直接计算出这个元素在集合中的位置,根本不需要一次又一次的查找!
举一个例子,假如我的数组A中,第i个元素里面装的key就是i,
那么数字3肯定是在第3个位置,数字10肯定是在第10个位置。
哈希表就是利用利用这种基本的思想,建立一个从key到位置的函数,然后进行直接计算查找。
场景三:Hash表在海量数据处理中有着广泛应用。
3.Hash Table特点:
Hash Table的查询速度非常的快,几乎是O(1)的时间复杂度。
hash就是找到一种数据内容和数据存放地址之间的映射关系。
4.散列法:
定义:元素特征转变为数组下标的方法。
问题:我想大家都在想一个很严重的问题:“如果两个字符串在哈希表中对应的位置相同怎么办?”,
毕竟一个数组容量是有限的,这种可能性很大。
解决该问题的方法很多,我首先想到的就是用“链表”。
我遇到的很多算法都可以转化成链表来解决,
只要在哈希表的每个入口挂一个链表,保存所有对应的字符串就OK了。
5.散列表的查找步骤:
当存储记录时,通过散列函数计算出记录的散列地址
当查找记录时,我们通过同样的是散列函数计算记录的散列地址,并按此散列地址访问该记录
ps:
关键字——散列函数(哈希函数)——散列地址
优点:一对一的查找效率很高;
缺点:一个关键字可能对应多个散列地址;需要查找一个范围时,效果不好。
散列冲突:不同的关键字经过散列函数的计算得到了相同的散列地址。
好的散列函数=计算简单+分布均匀(计算得到的散列地址分布均匀)
哈希表是种数据结构,它可以提供快速的插入操作和查找操作。
6.哈希表的优缺点:
优点:
不论哈希表中有多少数据,查找、插入、删除(有时包括删除)只需要接近常量的时间即0(1)的时间级。
实际上,这只需要几条机器指令。
哈希表运算得非常快,在计算机程序中,如果需要在一秒种内查找上千条记录通常使用哈希表
(例如拼写检查器)哈希表的速度明显比树快,树的操作通常需要O(N)的时间级。
哈希表不仅速度快,编程实现也相对容易。
如果不需要有序遍历数据,并且可以提前预测数据量的大小。
那么哈希表在速度和易用性方面是无与伦比的。
缺点:
它是基于数组的,数组创建后难于扩展,某些哈希表被基本填满时,
性能下降得非常严重,所以程序员必须要清楚表中将要存储多少数据
(或者准备好定期地把数据转移到更大的哈希表中,这是个费时的过程)。
7.其他方式的散列法:
定义:
元素特征转变为数组下标的方法就是散列法。
散列法当然不止一种,下面列出三种比较常用的:
第一种:除法散列法
最直观的一种,上面使用的就是这种散列法,公式:
index = value % 16
ps:学过汇编的都知道,求模数其实是通过一个除法运算得到的,所以叫“除法散列法”。
第二种:平方散列法
求index是非常频繁的操作,而乘法的运算要比除法来得省时
(对现在的CPU来说,估计我们感觉不出来),
所以我们考虑把除法换成乘法和一个位移操作。公式:
index = (value * value) >> 28 (右移,除以2^28。记法:左移变大,是乘。右移变小,是除。)
ps:如果数值分配比较均匀的话这种方法能得到不错的结果,
但我上面画的那个图的各个元素的值算出来的index都是0——非常失败。
也许你还有个问题,value如果很大,value * value不会溢出吗?
答案是会的,但我们这个乘法不关心溢出,因为我们根本不是为了获取相乘结果,而是为了获取index。
第三种:斐波那契(Fibonacci)散列法
平方散列法的缺点是显而易见的,所以我们能不能找出一个理想的乘数,而不是拿value本身当作乘数呢?答案是肯定的。如下:
对于16位整数而言,这个乘数是40503
对于32位整数而言,这个乘数是2654435769
对于64位整数而言,这个乘数是11400714819323198485
乘数的获取原理:
这几个“理想乘数”是如何得出来的呢?
这跟一个法则有关,叫黄金分割法则,而描述黄金分割法则的最经典表达式无疑就是著名的斐波那契数列,
即如此形式的序列:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377, 610, 987, 1597, 2584, 4181, 6765, 10946,…。
另外,斐波那契数列的值和太阳系八大行星的轨道半径的比例出奇吻合。
对我们常见的32位整数而言,公式:
index = (value * 2654435769) >> 28
如果用这种斐波那契散列法的话,那上面的图就变成这样了:
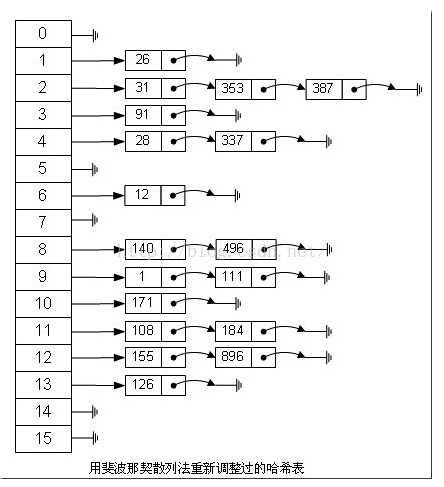
注:用斐波那契散列法调整之后会比原来的取摸散列法好很多。
适用范围:
快速查找,删除的基本数据结构,通常需要总数据量可以放入内存。
基本原理及要点:
hash函数选择,针对字符串,整数,排列,具体相应的hash方法。
碰撞处理,一种是open hashing,也称为拉链法;另一种就是closed hashing,也称开地址法,opened addressing。
8.散列冲突的解决方案:
一.建立一个缓冲区,把凡是拼音重复的人放到缓冲区中。当我通过名字查找人时,发现找的不对,就在缓冲区里找。
二.进行再探测。就是在其他地方查找。探测的方法也可以有很多种。
1.在找到查找位置的index的index-1,index+1位置查找,index-2,index+2查找,依次类推。这种方法称为线性再探测。
2.在查找位置index周围随机的查找。称为随机在探测。
3.再哈希。就是当冲突时,采用另外一种映射方式来查找。
总结:
这个程序中是通过取模来模拟查找到重复元素的过程。
对待重复元素的方法就是再哈希:对当前key的位置+7。
最后,可以通过全局变量来判断需要查找多少次。
我这里通过依次查找26个英文字母的小写计算的出了总的查找次数。
显然,当总的查找次数/查找的总元素数越接近1时,哈希表更接近于一一映射的函数,查找的效率更高。
9.扩展
d-left hashing中的d是多个的意思,我们先简化这个问题,看一看2-left hashing。
2-left hashing指的是将一个哈希表分成长度相等的两半,分别叫做T1和T2,给T1和T2分别配备一个哈希函数,h1和h2。
在存储一个新的key时,同时用两个哈希函数进行计算,得出两个地址h1[key]和h2[key]。
这时需要检查T1中的h1[key]位置和T2中的h2[key]位置,哪一个 位置已经存储的(有碰撞的)key比较多,然后将新key存储在负载少的位置。
如果两边一样多,比如两个位置都为空或者都存储了一个key,就把新key 存储在左边的T1子表中,2-left也由此而来。
在查找一个key时,必须进行两次hash,同时查找两个位置。
10.问题实例(海量数据处理)
我们知道hash 表在海量数据处理中有着广泛的应用,下面,请看另一道百度面试题:
题目:海量日志数据,提取出某日访问百度次数最多的那个IP。
方案:IP的数目还是有限的,最多2^32个,所以可以考虑使用hash将ip直接存入内存,然后进行统计。
11.示例(思路)
再看一遍原理:
理解哈希表的原理,其核心是理解所谓的哈希函数(散列函数)。
即如何构建一个确定的映射,它能把关键字映射到一个唯一的存储位置。
这种映射应该是我们可以进行计算的。
已知关键字,我们应该能算出其地址;反之,已知地址,我们可以检索到对应的关键字。
一旦建立起这种关系,那么给定关键字,我就能直接利用这个映射(即所谓的哈希函数)直接算出其地址并寻址。
这可大大缩减确定关键字存储位置所花的时间。
思路;
设要存储对象的个数为num, 那么我们就用len个内存单元来存储它们(len>=num);
以每个对象ki的关键字为自变量,用一个函数h(ki)来映射出ki的内存地址,也就是ki的下标,将ki对象的元素内容全部存入这个地址中就行了。
问题:Hash为什么这么想呢?换言之,为什么要用一个函数来映射出它们的地址单元呢?
回答:
示例描述:
现在我要你存储4个元素 13 7 14 11
显然,我们可以用数组来存。也就是:a[1] = 13; a[2] = 7; a[3] = 14; a[4] = 11;
当然,我们也可以用Hash来存。
下面给出一个简单的Hash存储:
第一步:
先来确定那个函数。
我们就用h(ki) = ki%5;(这个函数不用纠结,我们现在的目的是了解为什么要有这么一个函数)。
那么
对于第一个元素 h(13) = 13%5 = 3; 也就是说13的下标为3;即Hash[3] = 13;
对于第二个元素 h(7) = 7 % 5 = 2; 也就是说7的下标为2; 即Hash[2] = 7;
同理,Hash[4] = 14; Hash[1] = 11;
ps:好了,存现在是存好了。
但是,这并没有体现出Hash的妙处,也没有回答刚才的问题。
下面就让我来揭开它神秘的面纱吧。
第二步:现在我要你查找11这个元素是否存在。你会怎么做呢?
当然,对于数组来说,那是相当的简单,一个for循环就可以了。
也就是说我们要找4次。这是很笨的办法,因为为了找一个数需要把整个序列循环一遍才行,太慢!
下面我们来用Hash找一下。
首先,我们将要找的元素11代入刚才的函数中来映射出它所在的地址单元。
也就是h(11) = 11%5 = 1 了。
下面我们来比较一下Hash[1]?=11, 这个问题就很简单了。
也就是说我们就找了1次。我咧个去, 这个就是Hash的妙处了。
至此,刚才的问题也就得到了解答。至此,你也就彻底的明白了Hash了。
C++的LeetCode上的例子:
问题描述:
给定一个整数数组和一个目标值,找出数组中和为目标值的两个数。
你可以假设每个输入只对应一种答案,且同样的元素不能被重复利用。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
代码:
vector<int> twoSum(vector<int>& nums, int target) { vector<int> result; unordered_map<int, int> map; //the keys are nums's elements' values; map to subscripts. for(int i=0; i<nums.size(); i++) map[nums[i]] = i; //here you should think the i on the right side as a memory address. for(int i=0; i<nums.size(); i++){ //for example: nums ={3, 3}, target =6 int rest = target - nums[i]; if(map.find(rest) != map.end()){ int index = map[rest]; if(index == i) continue; if(index < i){ result = {index, i}; return result; }else{ result = {i, index}; return result; } } } }
补充:
1. 漏洞太多了,根本不是数据内容和存储地址的映射,是key(键值)和存储地址的映射,然后把value(值)也就是你说的数据内容存放到该存储地址上
学习来源:
https://blog.csdn.net/duan19920101/article/details/51579136
https://blog.csdn.net/qq_41230365/article/details/81058217




