BZOJ2815 拓扑排序 + LCA

https://www.lydsy.com/JudgeOnline/problem.php?id=2815

 

作为一个DAG图，结点之间又有这么明显的等级之分，很容易想到的是拓扑排序。

但是不管是正向的拓扑排序还是逆向的拓扑排序感觉都不是特别容易的能解决这个问题。

但事实上只要知道一个十分关键的点：一个物种会灭绝的必要条件是当且仅当另一个物种灭绝。

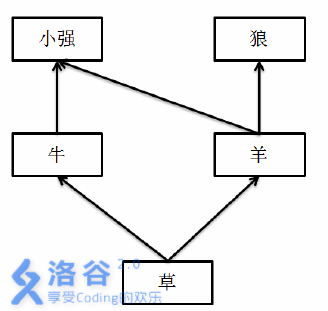例如样例给的图片当中，小强的灭绝仅和草是否灭绝有关，和牛羊无关。

因此事实上这个图的关系可以变为一棵树的关系，一个点会灭绝当且仅当他的祖先灭绝。

怎么确定一个点的父亲结点？考虑动态建树，以最底层的食物为起点开始拓扑排序，一个结点被访问意味着它所有的食物已经被加入树中，那么他的父亲就是他所有食物的LCA

最后求一个树的前缀和就可以了

一个小细节是倍增LCA需要一边建树一边维护稀疏表。

#include <map>
#include <set>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;
#define For(i, x, y) for(int i=x;i<=y;i++)  
#define _For(i, x, y) for(int i=x;i>=y;i--)
#define Mem(f, x) memset(f,x,sizeof(f))  
#define Sca(x) scanf("%d", &x)
#define Sca2(x,y) scanf("%d%d",&x,&y)
#define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define Scl(x) scanf("%lld",&x);  
#define Pri(x) printf("%d\n", x)
#define Prl(x) printf("%lld\n",x);  
#define CLR(u) for(int i=0;i<=N;i++)u[i].clear();
#define LL long long
#define ULL unsigned long long  
#define mp make_pair
#define PII pair<int,int>
#define PIL pair<int,long long>
#define PLL pair<long long,long long>
#define pb push_back
#define fi first
#define se second 
typedef vector<int> VI;
int read(){int x = 0,f = 1;char c = getchar();while (c<'0' || c>'9'){if (c == '-') f = -1;c = getchar();}
while (c >= '0'&&c <= '9'){x = x * 10 + c - '0';c = getchar();}return x*f;}
const double eps = 1e-9;
const int maxn = 1e5 + 10;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7; 
int N,M,K;
struct Edge{
    int to,next;
}edge[1000000],redge[maxn],tedge[maxn];
int head[maxn],tot;
int rhead[maxn],rtot;
int thead[maxn],ttot;
int pre[maxn];
void init(){
    for(int i = 0 ; i <= N ; i ++) rhead[i] = thead[i] = head[i] = -1;
    tot = rtot = ttot = 0;
}
void add(int u,int v){
    edge[tot].to = v;
    edge[tot].next = head[u];
    head[u] = tot++;
    redge[rtot].to = u;
    redge[rtot].next = rhead[v];
    rhead[v] = rtot++;
}
void tadd(int u,int v){
    tedge[ttot].to = v;
    tedge[ttot].next = thead[u];
    thead[u] = ttot++;
}
const int SP = 20;
int ind[maxn];
int pa[maxn][SP],dep[maxn];
void dfs(int u,int la){
    pre[u] = 0;
    for(int i = thead[u]; ~i ; i = tedge[i].next){
        int v = tedge[i].to;
        if(v == la) continue;
        dfs(v,u);
        pre[u] += pre[v] + 1;
    }
}
int lca(int u,int v){
    if(dep[u] < dep[v]) swap(u,v);
    int t = dep[u] - dep[v];
    for(int i = 0 ; i < SP; i ++) if(t & (1 << i)) u = pa[u][i];
    for(int i = SP - 1; i >= 0; i --){
        int uu = pa[u][i], vv = pa[v][i];
        if(uu != vv){
            u = uu;
            v = vv;
        }
    }
    return u == v ? u : pa[u][0];
}
int main(){
    Sca(N); init();
    for(int i = 1; i <= N ; i ++){
        int x;
        while(~scanf("%d",&x) && x){
            add(i,x);
            ind[i]++;
        }
    }
    int root = 0;
    pa[root][0] = 0; dep[root] = 1;
    for(int i = 1; i < SP; i ++) pa[root][i] = pa[pa[root][i - 1]][i - 1];
    queue<int>Q;
    for(int i = 1; i <= N ; i ++){
        if(!ind[i]){
            add(i,root);
            Q.push(i);
        }
    }
    while(!Q.empty()){
        int u = Q.front(); Q.pop();
        int fa = -1;
        for(int i = head[u]; ~i ; i = edge[i].next){
            int v = edge[i].to;
            if(~fa) fa = lca(fa,v);
            else fa = v;
        }
        tadd(fa,u);
        pa[u][0] = fa; dep[u] = dep[fa] + 1;
        for(int i = 1; i < SP ; i ++) pa[u][i] = pa[pa[u][i - 1]][i - 1];
        for(int i = rhead[u]; ~i ; i = redge[i].next){
            int v = redge[i].to;
            ind[v]--;
            if(!ind[v]) Q.push(v);
        }
    }
    dfs(root,-1);
    for(int i = 1; i <= N ; i ++) Pri(pre[i]);
    return 0;
}