LeetCode416. 分割等和子集

☆☆☆☆☆思路：转化为0-1背包问题。 即，是否可以从输入数组中挑出一些正整数，使得这些数的和 等于 整个数组和的一半。

　　本题与传统0-1背包问题的不同在于，传统0-1 背包问题要求 选取的物品的重量之和 不能超过 背包的容量；而本题选取的数字之和需要 恰好等于 规定的和的一半。

　　这一点的区别，决定了初始化时，所有值应为False。因此，本题状态转移方程为 F(i, c) = F(i - 1, c) || F(i - 1, c - w(i) )， 其中F(n , c)表示 考虑将n个物品填满容量为C的背包。时间复杂度为 O(n * sum/2) = O(n * sum)

 

　　Step1.状态定义：dp[i][j] 表示从数组的[0,i]下标范围内，选取若干正整数，是否存在一种选取方案使得被选取的正整数的和等于j， 初始时均为false。

　　Step2.考虑边界情况：

　　　　1. 如果不选取任何正整数，则被选取的正整数为0.因此，dp[i][0] = true

　　　　2.当i==0时，只有一个正整数nums[0]可以选取，因此，dp[0][nums(0)] = true。

　　Step3.状态转移：

　　

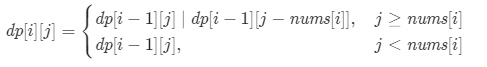
0-1背包，即数组中的元素不可重复使用。技巧为 nums放在外循环，target在内循环，且内循环倒序。

class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length;
        if (n < 2) return false;
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        // 如果和是奇数，则不能被平分
        if ((sum & 1) == 1) {
            return false;
        }
        /*
        int target = sum / 2;
        // dp[i][j] 表示从数组的[0,i]下标范围内，选取若干正整数，
        //          是否存在一种选取方案使得被选取的正整数的和等于j
        boolean[][] dp = new boolean[n][target + 1]; // 背包容量 0 ~ target
        for (int i = 0; i < n; i++) {
            dp[i][0] = true; // 不选取任何正整数，则被选取的正整数和为0
        }
        if (nums[0] <= target) {
            dp[0][nums[0]] = true;
        }
        for (int i = 1; i < n; i++) {
            for (int j = 1; j <= target; j++) {
                dp[i][j] = dp[i-1][j];
                if (j >= nums[i]) {
                    dp[i][j] |= dp[i-1][j-nums[i]];
                }
            }
        }
        return dp[n-1][target];
        */
        /**
         *  空间优化
         */
        int target = sum / 2;
        boolean[] dp = new boolean[target + 1];
        dp[0] = true;
        // 只考虑第一个num，看是否能填满对应的背包。
        if (nums[0] <= target) {
            dp[nums[0]] = true;
        }
//        for (int i = 0; i <= target; i++) {
//            dp[i] = (nums[0] == i);
//        }
        for (int i = 1; i < n; i++) {
            for (int j = target; j >= nums[i]; j--) { // 注意要倒序计算
                dp[j] = dp[j] || (dp[j-nums[i]]);
            }
        }
        return dp[target];
    }
}