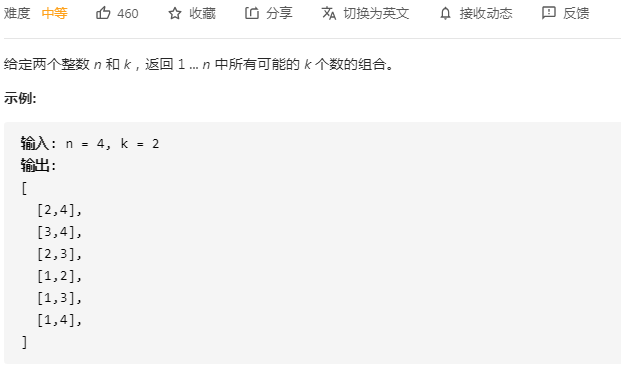
LeetCode77. 组合

☆☆☆思路：与排列问题不同，组合问题只需要从当前位置往后搜索。而排列问题每次都需要从头寻找，需要用vis数组记录访问过的元素。

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (n <= 0 || k <= 0 || k > n) return res;
        // 从1开始是题目的设定
        dfs(n, k, 1, new ArrayList<>(), res);
        return res;
    }
    // 求解C(n,k)，当前已经找到的组合存储在list中，需要从start开始搜索新元素。
    private void dfs(int n, int k, int start, List<Integer> list, List<List<Integer>> res) {
        if (list.size() == k) {
            res.add(new ArrayList<>(list));
            return;
        }
        /* 耗时：22ms
        for (int i = start; i <= n; i++) {
            list.add(i);
            // 下一轮搜索，设置的搜索起点要加 1，因为组合不允许出现重复的元素
            dfs(n, k, i + 1, list, res);
            list.remove(list.size() - 1);
        }
        */
        // 剪枝操作，只需要修改循环条件即可。 耗时：2ms
        // 优化：搜索起点有上界，如果n为7，k为4，从5开始搜已经没意义了
        // 进入循环前，当前还有k-list.size()个空位，所以，[i...n]中至少要有k-list.size()个元素
        // eg. 如果 k-list.size()-1等于1，那么i最大为n，如果等于2，那么i最大为n-1
        // 因此，i 最大为   n - (k - list.size()) + 1 ，不能超过它，否则后面没有足够的空位。
        for (int i = start; i <= n - (k-list.size()) + 1; i++) {
            list.add(i);
            dfs(n, k, i + 1, list, res);
            list.remove(list.size() - 1);
        }
    }
}