剑指07.斐波那契数列
题目描述
大家都知道斐波那契(Fibonacci)数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0,第1项是1)。
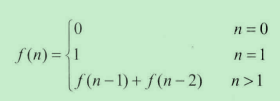 要求使用递归和非递归两种方法
要求使用递归和非递归两种方法
1.递归实现 时间复杂度:O(2n) ,空间复杂度:O(1)
public class Solution { public int Fibonacci(int n) { if(n<=0) return 0; if(n==1) return 1; return Fibonacci(n-1) + Fibonacci(n-2); } }
上述代码效率低,这样是拿不到Offer的(ㄒoㄒ)~~!! 上述递归代码之所以慢,是因为会大量重复计算相同的数。
2.非递归实现
2.1 版本1 时间复杂度:O(n),空间复杂度:O(1)
分析:如果自底向上使用动态规划的话,我们可以当前状态只和之前的两个状态有关,所以并不需要一个DP数组来存所有的状态,只需存储最近的两个数
- sum 存储第 n 项的值
- one 存储第 n-1 项的值
- two 存储第 n-2 项的值
public class Solution { public int Fibonacci(int n) { if(n<=0) return 0; if(n==1) return 1; int sum = 0; int one = 1; int two = 0; for(int i = 2; i <= n; i++){ sum = one + two; two = one; one = sum; } return sum; } }
2.2 版本2 时间复杂度:O(n),空间复杂度:O(1)
分析:观察2.1节版本1可以发现,其实还可以利用 sum 存储第 n-1 项
public class Solution { public int Fibonacci(int n) { if(n == 0){ return 0; }else if(n == 1){ return 1; } int sum = 1; int one = 0; for(int i=2;i<=n;i++){ sum = sum + one; one = sum - one; } return sum; } }
3.终极版本 时间复杂度为O(logn)
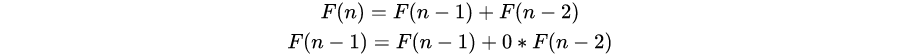
转化为矩阵运算可得
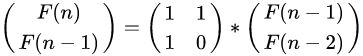
而右边的2*1矩阵又可以进一步分解为
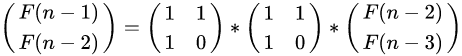
一直分解下去,直到右边的2*1矩阵位F(2),F(1),即
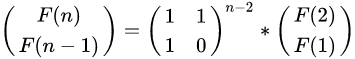
现在的问题转化为如何求矩阵的乘方,利用乘方的幂次奇偶性质,比如相求n次方,只需要求n/2平方,然后再平方以下即可。
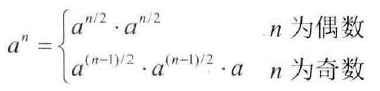
快速幂解法见【40讲系列6】递归、分治


