多元线性回归—波士顿房价预测(版本一)
背景:波士顿房价数据集包括506个样本,每个样本包括12个特征变量和该地区的平均房价。房价(单价)显然和多个特征变量相关,不是单变量线性回归(一元线性回归)问题;选择多个特征变量来建立线性方程,这就是多变量线性回归(多元线性回归)问题。
房价和多个特征变量相关,本案例尝试使用多元线性回归建模 Y=X1*W1+X2*W2+..+X12*W12+b
结果可以由不同特征的输入值和对应的权重相乘求和,加上偏置项计算求解,多变量线性方程可用矩阵运算表示。
一、数据读取
CRIM:城镇人均犯罪率 AGE:1940年之前建成的自用房屋比例
ZN:住宅用地超过25000sq.ft.的比例 DIS:到波士顿5个中心区域的加权距离
INDUS:城镇非零售商用土地的比例 RAD:辐射性公路的靠近指数
CHAS:边界是河流为1,否则0 TAX:每10000美元的全值财产税率
NOX:一氧化氮浓度 PTRATIO:城镇师生比例
RM:住宅平均房间数 LSTAT:人口中地位低下者的比例
标签数据 MEDV:自住房的平均房价,单位:干美元
1.1通过pandas读取数据文件,列出统计概述(分析用)

import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import pandas as pd from sklearn.utils import shuffle #打乱样本 df = pd.read_csv("data/boston.csv", header=0) print(df.describe()) #线束数据摘要描述信息
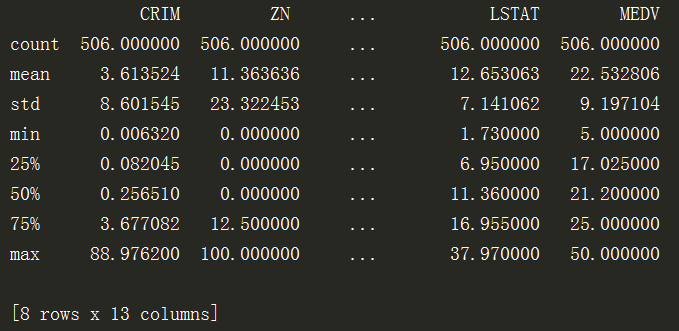
pandas是python提供的非常好用的数据分析模块,但是在使用pandas进行数据分析时,有时候需要查看打印的结果,当dataframe行数或者列数比较多的时候,打印结果总是有一些省略号,不能完整的看到数据的大致分布,比如最大值,最小值,等等,了解数据分布的区间有助于进行可视化和进一步分析。查看pandas的文档,这个问题可以通过pandas内置的set_option()方法解决,从文档的属性设置中可以看到,与显示的行数列数有关的选项主要是【display】中的【max_columns,max_rows,max_colwidth,line_width】等这几项,只需要将这几项属性值设置得大一些就可以解决。
修改后的程序为:

import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import pandas as pd from sklearn.utils import shuffle #打乱样本 pd.set_option('display.max_columns',1000) pd.set_option('display.width',1000) pd.set_option('display.max_colwidth',1000) df = pd.read_csv("data/boston.csv", header=0) print(df.describe()) #线束数据摘要描述信息(数量、平均值、标准值、最大最小值等)

从上到下分别为,每一列的数目、平均值、标准值、最小值、25%位置的值、50%位置的值、75%位置的值、最大值。
1.2载入本例所需数据
df = df.values #获取df的值
df = np.array(df) #把df转换为np的数组格式
# print(df)
x_data = df[:,:12] #x_data为前12列特征数据
y_data = df[:,12] #y_data为第12列标签数据
# print(x_data,'\n shape=',x_data.shape)
# print(y_data,'\n shape=',y_data.shape)
二、模型定义
2.1定义特征数据和标签数据的占位符
x = tf.placeholder(tf.float32,[None,12],name ="X") #12个特征数据(12列)
y = tf.placeholder(tf.float32,[None,1],name ="Y") #1个标签数据(1列)
Note:shape中None表示行的数量未知,在实际训练时决定一次代入多少行样本,从一个样本的随机SDG到批量SDG都可以.
2.2定义模型结构
#定义了一个命名空间,对以下语句的节点打包在一起,使计算图看上去更简洁 with tf.name_scope("Model"): # w 初始化值为shape=(12,1)的随机数,标准差为0.01 w = tf.Variable(tf.random_normal([12,1],stddev=0.01),name="W") b = tf.Variable(1.0, name="b") # b 初始化值为1.0 def model(x, w, b): # w 和 b 四矩阵相乘,用matmul,不能用mutiply或者* return tf.matmul(x,w) + b pred = model(x, w, b) #预测计算操作,前向计算节点
三、训练模型
3.1设置训练参数(超参数)
train_epochs = 50 #迭代次数(训练轮数)
learning_rate = 0.01 #学习率,设置为经验值。
3.2定义均方差损失函数
with tf.name_scope("LossFunction"):
loss_function = tf.reduce_mean(tf.pow(y-pred, 2)) #均方误差
3.3选择优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function) #创建优化器
Note:常用优化器包括
tf.train.MomentumOptimizer tf.train.AdamOptimizer
tf.train.GradientDescentOptimizer tf.train.FtrlOptimizer
tf.train.AdadeltaOptimizer tf.train.ProximalGradientDescentOptimizer
tf.train.AdagradOptimizer tf.train.ProximalAdagradOptimizer
tf.train.AdagradDAOptimizer tf.train.RMSPropOptimizer
3.4声明并启动会话
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
3.5迭代训练
1 for epoch in range (train_epochs): 2 loss_sum = 0.0 3 for xs, ys in zip(x_data,y_data): # 每次各取一行数据(一维) 4 xs = xs.reshape(1,12) # feed数据必须和placeholder的shape一致 5 ys = ys.reshape(1,1) 6 _, loss = sess.run([optimizer,loss_function],feed_dict={x: xs, y: ys}) 7 loss_sum= loss_sum+ loss 8 xvalues,yvalues = shuffle(x_data,y_data) #打乱数据顺序 9 bOtemp=b.eval(session=sess) 10 wOtemp=w.eval(session=sess) 11 loss_average =loss_sum/len(y_data) 12 print("epoch=",epoch+1,"loss=",loss_average,"b=",betemp,"w=",wOtemp)
Note:第四行和第五行的解释,一维变为二维,如把[x1,x2,...x12]变成[[x1,x2,...x12]] 进而满足之前定义的[None,12] ; 18 变为[[18]]进而满足之前定义的[None,1]
以上完整程序,运行后结果为:

可以发现,训练结果出现了异常!
四、探究训练结果异常的原因
要考虑不同特征值取值范围大小的影响,机器学习过程中需要避免特征的绝对值取值范围大小,造成权值过大的影响,需要进行归一化。
归一化[0~1]:特征值 /(特征值max - 特征值min)
4.1特征数据归一化
对1.2节代码进行修改,其余代码不变
#对特证数据【0-11】列归一化 for i in range(12): df[:,i]=df[:,i]/(df[:,i].max() - df[:,i].min()) x_data = df[:,:12] #xdata为归一化后的前12列特征数据 y_data = df[:,12] #ydata 为最后1列标签数据
运行后,取最后一轮训练结果显示为:

Note:权重绝对值越大说明该特征值影响越大。
五、模型应用
模型一般应该用来预测新的样本的值,本例506条数据都用来训练了,暂时没有新的数据。
n=348 #指定一条来看看效果 # n=np.random.randint(506) #随机确定一条来看看效果 # print(n) x_test = x_data[n] x_test = x_test.reshape(1,12) predict = sess.run(pred, feed_dict={x:x_test}) print("预测值:%f" % predict) target = y_data[n] print("标签值:%f" % target)
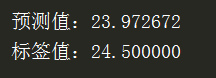
完整代码为:

#Created by:Huang #Time:2019/10/8 0007. import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import pandas as pd from sklearn.utils import shuffle #打乱样本 # pd.set_option('display.max_columns',1000) # pd.set_option('display.width',1000) # pd.set_option('display.max_colwidth',1000) df = pd.read_csv("data/boston.csv", header=0) # print(df.describe()) #线束数据摘要描述信息(数量、平均值、标准值、最大最小值等) df = df.values #获取df的值 df = np.array(df) #把df转换为np的数组格式 # print(df) #对特证数据【0-11】列归一化 for i in range(12): df[:,i]=df[:,i]/(df[:,i].max() - df[:,i].min()) x_data = df[:,:12] #xdata为归一化后的前12列特征数据 y_data = df[:,12] #ydata 为最后1列标签数据 # print(x_data,'\n shape=',x_data.shape) # print(y_data,'\n shape=',y_data.shape) x = tf.placeholder(tf.float32,[None,12],name ="X") #12个特征数据(12列) y = tf.placeholder(tf.float32,[None,1],name ="Y") #1个标签数据(1列) #定义了一个命名空间,对以下语句的节点打包在一起,使计算图看上去更简洁 with tf.name_scope("Model"): # w 初始化值为shape=(12,1)的随机数,标准差为0.01 w = tf.Variable(tf.random_normal([12,1],stddev=0.01),name="W") b = tf.Variable(1.0, name="b") # b 初始化值为1.0 def model(x, w, b): # w 和 b 四矩阵相乘,用matmul,不能用mutiply或者* return tf.matmul(x,w) + b pred = model(x, w, b) #预测计算操作,前向计算节点 train_epochs = 50 #迭代次数(训练轮数) learning_rate = 0.01 #学习率,设置为经验值。 with tf.name_scope("LossFunction"): loss_function = tf.reduce_mean(tf.pow(y-pred,2)) #均方误差 optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function) #创建优化器 sess = tf.Session() init = tf.global_variables_initializer() sess.run(init) for epoch in range (train_epochs): loss_sum = 0.0 for xs, ys in zip(x_data,y_data): # 每次各取一行数据(一维) xs = xs.reshape(1,12) # feed数据必须和placeholder的shape一致 ys = ys.reshape(1,1) _, loss = sess.run([optimizer,loss_function],feed_dict={x: xs, y: ys}) #下划线表示只接收但之后并不会去用,返回值对我们没有用 loss_sum= loss_sum+ loss xvalues,yvalues = shuffle(x_data,y_data) #每训练一轮(506个数据),打乱数据顺序 b0temp = b.eval(session=sess) wOtemp = w.eval(session=sess) loss_average =loss_sum/len(y_data) print("epoch=",epoch+1,"loss=",loss_average,"b=",b0temp,"w=",wOtemp) # n=348 #指定一条来看看效果 n=np.random.randint(506) #随机确定一条来看看效果 print(n) x_test = x_data[n] x_test = x_test.reshape(1,12) predict = sess.run(pred, feed_dict={x:x_test}) print("预测值:%f" % predict) target = y_data[n] print("标签值:%f" % target)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号