单纯形表的简单方法。

线性规划常用的方法是单纯形表法，下面用一个简单的例子告诉大家如何用最简单的方法求取目标函数Z值。

用单纯形方法求解线性规划问题 ：

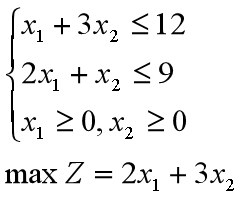
首先引入松弛变量 ，把原问题化为 标准形式：

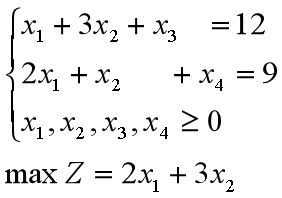
具体步骤如下： 第1步，确定初始单纯形表

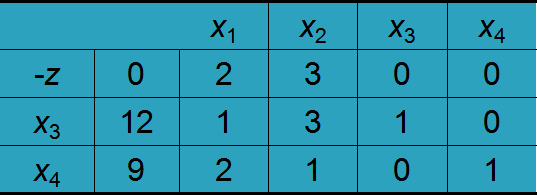
第2步：

判别检验所有的检验系数 （1）如果所有的检验系数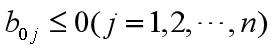

, 则由最优性判定定理知，已获最优解，即此时的基本可行解就是最优解。 （2）若检验系数中，有些为正数，但其中某一正的检验系数所对应的列向量的各分量均非正，则线性规划问题无解。 （3）若检验系数中，有些为正数，且它们所对应的列向量中有正的分量，则需要换基、进行迭代运算。

  而在此可以看出b01=2, b02=3，所以b1不是最优基，进行换基迭代。

第3步，选主元。 根据选主元法则，首先选择检验系数最大的是X2列，其次用0列即系数列比上X2列，数值小的即为主元，在这里很明显可以知道主元是。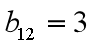

第4步，进行初等变换，让主元b12值变为1，主元所在列的其他数值为0。得到

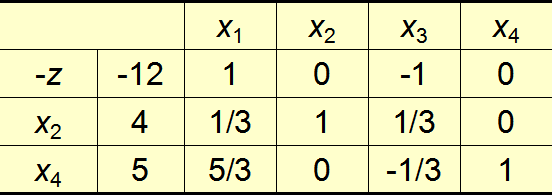
此时发现b01=1>0,重复上面步骤，(此时主元是b21=5/3) :

 

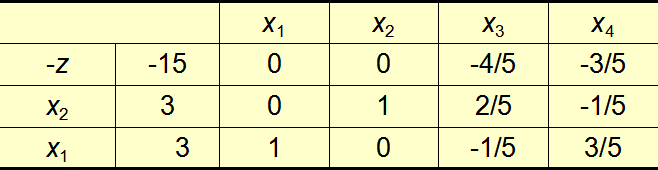
这时检验系数为负数，

检验各检验数可知得最优解X1=3,X2=3, X3=0, X4=0:目标函数最大值为 Z=15。