三角恒等变换
三角恒等变换
三角函数和单位圆关系
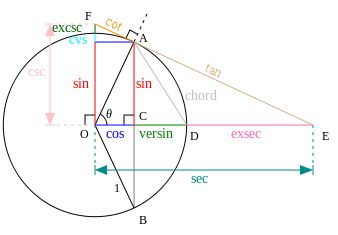
同角三角函数的关系
解释:同角即终边相同的角。
-
平方关系
\[sin^2(\alpha) + cos^2(\alpha) = 1 \] -
商数关系
\[tan(\alpha) = \frac{sin(\alpha)}{cos(\alpha)} \]
三角函数诱导公式
下列公式中,字母\(k\)满足\(k \in z\)的条件。
公式一
\[sin(\alpha + 2k\pi) = sin(\alpha)
\]
\[cos(\alpha + 2k\pi) = cos(\alpha)
\]
\[tan(\alpha + 2k\pi) = tan(\alpha)
\]
公式二
\[sin(\alpha + \pi) = -sin(\alpha)
\]
\[cos(\alpha + \pi) = -cos(\alpha)
\]
\[tan(\alpha + \pi) = \tan(\alpha)
\]
公式三
\[sin(-\alpha) = -sin(\alpha)
\]
\[cos(-\alpha) = cos(\alpha)
\]
\[tan(-\alpha) = -tan(\alpha)
\]
公式四
\[sin(\pi - \alpha) = sin(\alpha)
\]
\[cos(\pi - \alpha) = -cos(\alpha)
\]
\[tan(\pi - \alpha) = -tan(\alpha)
\]
公式五
\[sin(2\pi - \alpha) = -sin(\alpha)
\]
\[cos(2\pi - \alpha) = cos(\alpha)
\]
\[tan(2\pi - \alpha) = -tan(\alpha)
\]
公式六
\[sin(\frac{\pi}{2} - \alpha) = cos(\alpha)
\]
\[cos(\frac{\pi}{2}) = sin(\alpha)
\]
公式七
\[sin(\alpha + \frac{\pi}{2}) = cos(\alpha)
\]
\[cos(\alpha + \frac{\pi}{2}) = -sin(\alpha)
\]
三角函数和(差)角公式
sin公式
\[sin(\alpha + \beta) = sin(\alpha)cos(\beta) + cos(\alpha)sin(\beta)
\]
\[sin(\alpha - \beta) = sin(\alpha)cos(\beta) - cos(\alpha)sin(\beta)
\]
\[sin(2\alpha) = 2sin(\alpha)cos(\alpha) = 2sin(\alpha)\sqrt{1 - sin^2(\alpha)}
\]
cos公式
\[cos(\alpha + \beta) = cos(\alpha)cos(\beta) - sin(\alpha)sin(\beta)
\]
\[cos(\alpha - \beta) = cos(\alpha)cos(\beta) + sin(\alpha)sin(\beta)
\]
对于\(cos\)而言,\(cos(\alpha - \beta)\)和\(cos(\beta - \alpha)\)是一样的,因为根据诱导公式有\(-cos(\alpha) = cos(\alpha)\)。
\[cos(2\alpha) = cos^2(\alpha) - sin^2(\alpha) = 1 - 2cos^2(\alpha) = 1 - 2sin^2(\alpha)
\]
tan公式
\[tan(\alpha + \beta) = \frac{tan(\alpha) + tan(\beta)}{1 - tan(\alpha)tan(\beta)}
\]
\[tan(\alpha - \beta) = \frac{tan(\alpha) - tan(\beta)}{1 + tan(\alpha)tan(\beta)}
\]
\[tan(2\alpha) = \frac{2tan(\alpha)}{1 - tan^2(\alpha)}
\]
半角公式(降幂公式)
根据\(cos\)的二倍角公式,可以得到半角公式。
sin公式
\[sin^2(\alpha) = \frac{1 - cos(2\alpha)}{2}
\]
cos公式
\[sin^2(\alpha) = \frac{1 + cos(2\alpha)}{2}
\]
tan公式
根据商数关系以及以上两条公式可得:
\[tan^2(\alpha) = \frac{1 - cos(2\alpha)}{1 + cos(2\alpha)}
\]
换一种写法
以上的公式又经常写为半角的形式。
\[sin(\frac{\alpha}{2}) = \frac{1 - cos(\alpha)}{2}
\]
\[cos(\frac{\alpha}{2}) = \frac{1 + cos(\alpha)}{2}
\]
\[tan(\frac{\alpha}{2}) = \frac{1 - cos(\alpha)}{1 + cos(\alpha)}
\]
积化和差与和差化积
通过对三角函数的和(差)公式可以得到三角函数的积化和差与和差化积公式。
\[sin(\alpha)cos(\beta) = \frac{1}{2}(sin(\alpha + \beta) - sin(\alpha - \beta))
\]
\[cos(\alpha)sin(\beta) = \frac{1}{2}(sin(\alpha + \beta) + sin(\alpha - \beta))
\]
\[cos(\alpha)cos(\beta) = \frac{1}{2}(cos(\alpha + \beta) - cos(\alpha - \beta))
\]
\[sin(\alpha)sin(\beta) = \frac{1}{2}(cos(\alpha + \beta) + cos(\alpha - \beta))
\]
同理,若令\(x = \alpha + \beta\)、\(y = \alpha - \beta\),则可以推到得到:
\[\beta = \alpha - y = x - \alpha \\
\alpha = \frac{x + y}{2} \\
\beta = \frac{x - y}{2}
\]
将\(x\)和\(y\)取代上述公式中的\(\alpha\)和\(\beta\),可得和差化积公式:
\[sin(x) - sin(y) = 2sin(\frac{x + y}{2})cos(\frac{x - y}{2})
\]
\[sin(x) + sin(y) = 2cos(\frac{x + y}{2})sin(\frac{x - y}{2})
\]
\[cos(x) - cos(y) = 2cos(\frac{x + y}{2})cos(\frac{x - y}{2})
\]
\[cos(x) + cos(y) = 2sin(\frac{x + y}{2})sin(\frac{x - y}{2})
\]
万能公式
下列公式中,\(t\)为:
\[t(\alpha) = tan(\frac{\alpha}{2})
\]
函数\(t\)值域为整个实数域,万能公式把三角函数转换为只含有\(t\)的代数式,建立起了代数和三角函数的关系。
sin公式
\[sin(\alpha) = \frac{2t(\alpha)}{1 + t^2(\alpha)}
\]
cos公式
\[cos(\alpha) = \frac{1 - t^2(\alpha)}{1 + t^2(\alpha)}
\]
tan公式
\[tan(\alpha) = \frac{2t(\alpha)}{1 - t^2(\alpha)}
\]


