机器学习---逻辑回归（一）（Machine Learning Logistic Regression I）
逻辑回归（Logistic Regression）是一种经典的线性分类算法。逻辑回归虽然叫回归，但是其模型是用来分类的。
让我们先从最简单的二分类问题开始。给定特征向量x=([x1,x2,...,xn])T以及每个特征的权重w=([w1,w2,...,wn])T，阈值为b，目标y是两个分类标签---1和-1。为了便于叙述，把b并入权重向量w，记作
，特征向量则扩充为
。（为了简便的缘故，下面还是都写成w和x）
事实上，我们已经学习过一种分类算法了。在《机器学习---感知机（Machine Learning Perceptron）》一文中，我们知道感知机是将线性方程式嵌套入符号函数，其对目标y的估计是：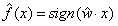
。如果样本的wx>0，那么估计其目标是1 ，如果样本的wx<0，那么估计其目标是-1。如下图所示，可以看出sign函数其实是一种单位阶跃函数。这样的分类是比较粗糙的，因为你不知道分类阈值0附近的情况。比如说如果训练集的类别不均衡，那么分类平面肯定会向类别多的那一边靠拢，如果我们想要结果比较“公正”，就需要根据情况设定不同的分类阈值。此外，感知机解决的是“硬分类”问题，即分类结果就是目标函数的决策结果，而另外一类称为“软分类”问题，即目标函数输出的是不同类别对应的概率，最后的分类结果为概率最大的类。显然，我们需要不同的算法来解决“软分类”问题。因此，最好能把阶跃函数变成连续函数，把线性方程映射到这个函数上，并且能让这个函数上的每个点代表分类概率。
（注：wx是特征向量和权重向量的点积/内积，wx=w1x1+w2x2+...+wnxn）
阶跃函数（step function）：
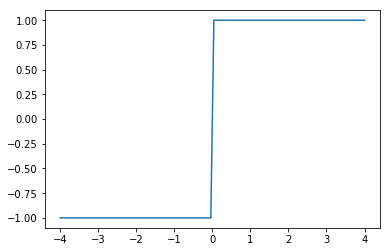
有人想到正态分布的累积分布函数符合这个要求，其函数上的点代表累积概率，比如P(y=1|x<value)，其对应的模型被称之为probit回归模型。但是由于这个函数比较复杂（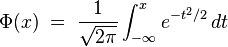
），而且不是太容易解释，这限制了它的应用。
因此，我们最好能找到和正态分布的累积分布函数近似的函数。又有人发现逻辑分布的累积分布函数和正态分布的累积分布函数几乎一样，并且逻辑分布的累积分布函数比较简单（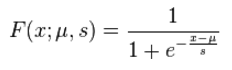
），而且函数上的点可以用来表示概率。
正态分布的累积分布函数和最佳逻辑分布的累积分布函数：
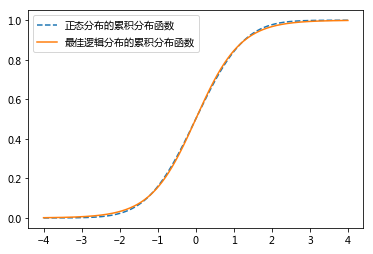
人们选择使用标准逻辑分布的累积分布函数作为映射函数，其在学术上被称为sigmoid函数。
sigmoid函数：
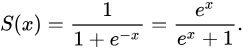
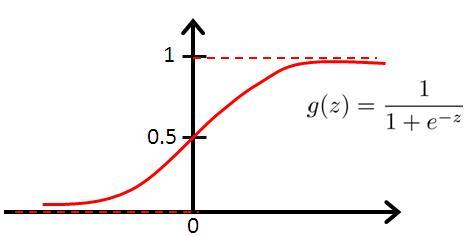
把线性组合wx代入sigmoid函数就得到逻辑函数（logistic fuction），其对应的模型叫logit回归模型，也叫logistic回归模型：
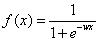
逻辑函数上的点对应的就是给定特征x，目标为1的条件概率：
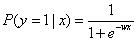
分类阈值可以根据实际情况选择。假如我们选择0.5作为分类阈值来划分，那么如果样本f(x)>0.5，我们估计其目标为1，如果样本f(x)<0.5，我们估计其目标为-1。如果把对y的估计写成和感应机一样的形式，那就是
。
在接下去之前我们先思考几个问题：
1. sigmoid函数是怎么得来的？
因为目标y是两个分类标签，因此我们假设y服从伯努利分布（y不是0就是1），y=1的概率为p，那么目标y的概率质量函数就是：
，将其写成条件概率表达式就是：
。
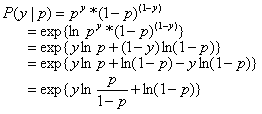
而指数分布族的一般表达式为：
。
如果令：θ=p，h(x)=1，T(x)=x，η(θ)=lnp/(1−p)，A(θ)=−ln(1−p)。那么，伯努利分布就属于指数分布族。
从上面可知：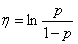
，因此：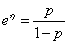
。
最后可以推导出：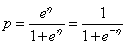
。
此外，sigmoid函数很自然地出现在贝叶斯法的后验概率（二分类问题）表达式里：
2. 为什么逻辑回归称作回归？
除去历史的原因，是因为逻辑回归本质上是一个线性回归模型，其线性组合表示分类为1的对数几率。
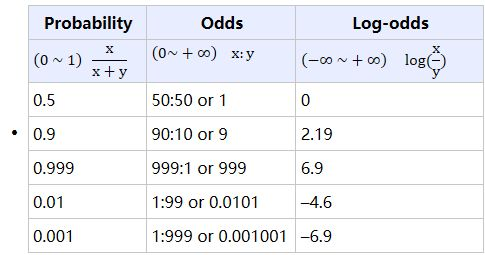
什么是几率？人们用事件发生与不发生的比值来表示事件发生的几率（odds）。假设事件发生的概率是 p ，那么事件发生的几率（odds）就是 p/(1-p) 。 odds 的值域从 0 到正无穷，几率越大，表示事件发生的可能性越大。
假设给定样本的特征值，该样本属于类别1的概率为：P(y=1|x)。因为只有两种可能的分类，因此样本属于另一类的概率为：1-P(y=1|x)。
代入几率计算公式后得到样本属于类别1的几率：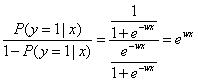
两边取自然对数：
上述变换称为logit变换。此时等式的左边我们称之为对数几率（Log Odds），而等式的右边就是线性回归方程。因此，周志华老师在其西瓜书中称逻辑回归算法为对数几率回归，因为他觉得对数几率回归这个名称更能反映算法的本质。
3. 为什么逻辑函数上的点可以用来表示分类概率？
因为wx的值域从负无穷大到正无穷大，正好对应对数几率的值域（见下图），而我们想要把wx映射到某种函数上，使得函数上的点可以代表概率，值域在0~1之间。因此，我们让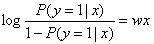
，然后逐渐变换，最后可以得到
，这个函数就是逻辑函数，因此逻辑函数上的点可以用来代表分类概率。（上述变换过程实际上就是logit变换的逆过程）
现在我们已经搞清了逻辑回归的本质，接下来就要对参数进行估计。估计出参数w，我们就可以得到逻辑回归模型。
因为目标y是两个分类标签，因此我们假设y服从伯努利分布（y不是0就是1），那么目标y的概率质量函数就是：
，将其写成条件概率表达式就是：
。
假设有m个独立样本，那么m个y之间也是相互独立的。因此，目标y的联合概率为：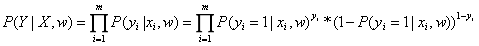
。然后我们可以用极大似然估计法来求解。
先来回忆一下什么是极大似然估计法：极大似然估计法就是去找到能使模型产生出样本数据的概率最大的参数θ，也就是找到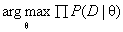
。由于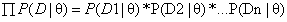
有连乘运算，通常对似然函数取对数计算，就可以把连乘变成求和，然后求导，取导数为0的极值点，就是想找的参数值。
因此，参数w的估计值就是：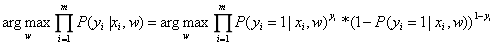
。
对似然函数取自然对数：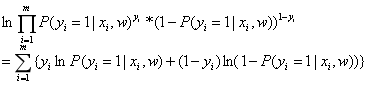
；
参数w的估计值可以写成：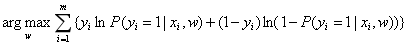
。
因为我们一般用梯度下降法求解，因此给上式加上负号，参数w的估计值也就是：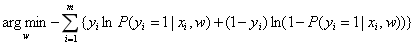
。
这个损失函数也被称为交叉熵（cross entropy）：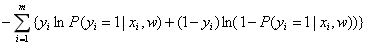
，可以把它看成两个概率分布之间的相似度，为了使估计的概率分布离真实的概率分布最接近，也就相当于让这个损失函数达到最小值。
接着我们把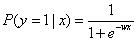代入损失函数：
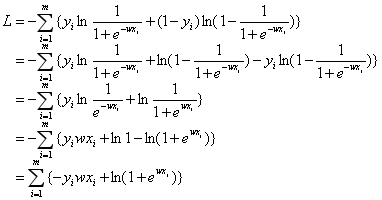
根据求导规则：
，
以及链式法则，对损失函数L求偏导可以得到：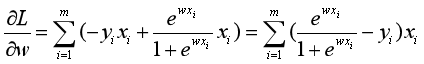
。
只有当数据线性可分时，上式等于0才有解析解。否则，我们只能用梯度下降法等迭代算法对参数进行优化。批量梯度下降法参数更新公式为：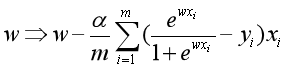
。
此外，用另一种方法可以推导得到损失函数的另一种形式，但是其本质都是一样的。假设目标y分为1和-1两类，那么我们可以得知：
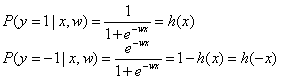
目标y的概率密度函数就是：h(yx)，将其写成条件概率表达式就是：
。
然后还是用极大似然估计法，对似然函数取自然对数及负号，那么损失函数L就是：
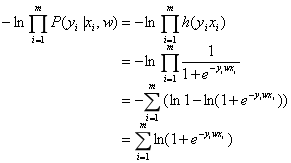
对损失函数L求偏导可以得到：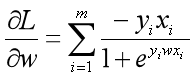
。
批量梯度下降法参数更新公式为：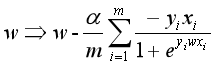
。
逻辑回归的优点：（摘自周志华西瓜书）
- 直接对分类的可能性进行建模，无需事先假设数据的分布，这样就避免了假设分布不准确所带来的问题
- 不仅能预测出类别，还能给出近似的概率预测值，这对许多需要利用概率辅助决策的任务很有用
- 逻辑函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解
逻辑回归的缺点：对数据特征间的独立性要求较高；不适用于特征和目标为非线性关系的数据中；当特征空间很大、特征有缺失时，逻辑回归的性能不是很好
