如何计算假设检验的功效（power）和效应量（effect size）？

做完一个假设检验之后，如果结果具有统计显著性，那么还需要继续计算其效应量，如果结果不具有统计显著性，并且还需要继续进行决策的话，那么需要计算功效。

 

功效（power）：正确拒绝原假设的概率，记作1-β。

假设检验的功效受以下三个因素影响：

• 样本量 (n)：其他条件保持不变，样本量越大，功效就越大。
• 显著性水平 (α)： 其他条件保持不变，显著性水平越低，功效就越小。
• 两总体之间的差异：其他条件保持不变，总体参数的真实值和估计值之间的差异越大，功效就越大。也可以说，效应量（effect size）越大，功效就越大。

 

应用：根据显著性水平α，效应量和样本容量n，计算功效。

（可用G*Power或Statsmodels计算）

单样本t检验：statsmodels.stats.power.tt_solve_power(effect_size=None, nobs=None, alpha=None, power=None, alternative='two-sided')

独立样本t检验：statsmodels.stats.power.tt_ind_solve_power(effect_size=None, nobs1=None, alpha=None, power=None, ratio=1.0, alternative='two-sided')

卡方检验：statsmodels.stats.power.GofChisquarePower.solve_power(effect_size=None, nobs=None, alpha=None, power=None, n_bins=2)

F检验：statsmodels.stats.power.FTestPower.solve_power(effect_size=None, df_num=None, df_denom=None, nobs=None, alpha=None, power=None, ncc=1)

方差分析：statsmodels.stats.power.FTestAnovaPower.solve_power(effect_size=None, nobs=None, alpha=None, power=None, k_groups=2)

 

效应量（effect size）： 样本间差异或相关程度的量化指标。

效应量通常用三种方式来衡量：(1) 标准均差（standardized mean difference），(2) 几率（odd ratio），(3) 相关系数（correlation coefficient）。

 

这里说一下第一种：标准均差（standardized mean difference）。主要有以下几种指标：

 

Cohen’s d : 两总体均值之间的标准差异。适用于两组样本的样本量和方差相似的情况。

计算公式：

其中：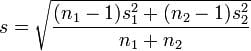

 

 

Hedges’ g: 是cohen的方法的改进，适用于两组样本的样本量不同的情况。

计算公式：

其中：

 

Glass’s Δ （delta）: 和cohen的方法类似，但是只除以控制组的标准差。适用于两组样本的方差不同的情况。

计算公式：

 

Cramer’s φ (Phi) or Cramer’s V: 用于测算类别型数据的效应量。当类别型变量包含2个类别时，使用Cramer’s phi，如果超过2个类别，那么使用Cramer’s V。

 

Cohen’s f2: 用于测算方差分析，多元回归之类的效应量。

计算公式：

 

应用：根据显著性水平α，功效和样本容量n，计算效应量。

（可用G*Power或Statsmodels计算）

单样本t检验：statsmodels.stats.power.tt_solve_power(effect_size=None, nobs=None, alpha=None, power=None, alternative='two-sided')

独立样本t检验：statsmodels.stats.power.tt_ind_solve_power(effect_size=None, nobs1=None, alpha=None, power=None, ratio=1.0, alternative='two-sided')

卡方检验：statsmodels.stats.power.GofChisquarePower.solve_power(effect_size=None, nobs=None, alpha=None, power=None, n_bins=2)

F方差齐性检验：statsmodels.stats.power.FTestPower.solve_power(effect_size=None, df_num=None, df_denom=None, nobs=None, alpha=None, power=None, ncc=1)

方差分析：statsmodels.stats.power.FTestAnovaPower.solve_power(effect_size=None, nobs=None, alpha=None, power=None, k_groups=2)

 

以上两种应用都属于事后检验（post hoc）。除此之外，还有一个应用就是：根据显著性水平α，功效和效应量，计算样本容量n。这属于事前检验（prior）。具体请见：《如何确定假设检验的样本量？》。

 

参考：

https://wenku.baidu.com/view/d78a82ecb9d528ea80c7792c.html

https://www.statisticssolutions.com/statistical-analyses-effect-size/