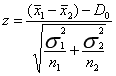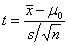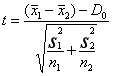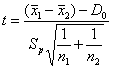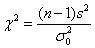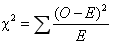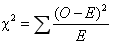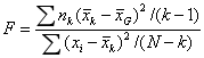假设检验总结以及如何用python进行假设检验(scipy)
几种常见的假设检验总结如下:
|
假设检验名称 |
Z检验 |
t检验 |
χ2检验 |
F检验 |
|
原假设 |
H0: μ≥μ0 H0: μ≤μ0 H0: μ=μ0 (比较样本和总体均值) H0: μ1-μ2≥0 H0: μ1-μ2≤0 H0: μ1-μ2=0 (比较两样本均值) H0: μd≥0 H0: μd≤0 H0: μd=0 (比较两样本差值均值和假设差值) |
H0: σ2≥σ02 H0: σ2≤σ02 H0: σ2=σ02 (比较样本和总体方差) H0: σ12≤σ22 H0: σ12=σ22 (比较两样本方差,即方差齐性) H0: 两类别型变量相互独立 (独立性检验) H0: 总体服从某个概率分布 (拟合优度检验) H0: 总体均值都相等 (方差分析)--- 通常用于三个及以上的样本 |
||
|
备择假设 |
Ha: μ<μ0 Ha: μ>μ0 Ha: μ≠μ0 (比较样本和总体均值) Ha: μ1-μ2<0 Ha: μ1-μ2>0 Ha: μ1-μ2≠0 (比较两样本均值) Ha: μd<0 Ha: μd>0 Ha: μd≠0 (比较两样本差值均值和假设差值) |
Ha: σ2<σ02 Ha: σ2>σ02 Ha: σ2≠σ02 (比较样本和总体方差) Ha: σ12>σ22 Ha: σ12≠σ22 (比较两样本方差) Ha: 两类别型变量不独立 (独立性检验) Ha: 总体不服从某个概率分布 (拟合优度检验) Ha: 总体均值不全相等 (方差分析)--- 通常用于三个及以上的样本 |
||
|
检验类型 |
左尾 右尾 双尾 |
左尾 右尾 双尾 |
||
|
检验先决条件 |
σ已知,总体服从正态分布,若总体分布不服从正态分布,那么样本量需大于等于30 |
σ未知,样本量可以小于30(当总体服从正态分布时),样本量大于等于30(总体分布不服从正态分布) |
各期望频数大于5(独立性检验,拟合优度检验) |
独立样本,总体近似正态分布(比较两样本方差,即方差齐性) 独立样本,总体近似正态分布,总体方差相似(方差分析) |
|
检验统计量 |
|
独立样本,两样本方差不相等)
独立样本,两样本方差相等)
配对样本) |
|
|
|
决策方法 |
临界值法:如果z ≤ -zα,则拒绝原假设(左尾) 如果z ≥ zα,则拒绝原假设(右尾) 如果z ≤ -zα/2 或 z ≥ zα/2,则拒绝原假设(双尾) (如果置信区间不包含μ0,则拒绝原假设) p值法:如果p值≤α,则拒绝原假设 |
临界值法:如果t ≤ -tα,则拒绝原假设(左尾) 如果t ≥ tα,则拒绝原假设(右尾) 如果t ≤ -tα/2 或 t ≥ tα/2,则拒绝原假设(双尾) (如果置信区间不包含μ0,则拒绝原假设) p值法:如果p值≤α,则拒绝原假设 |
临界值法:如果χ2 ≤ χ2(1-α),则拒绝原假设(左尾) 如果χ2 ≥ χ2α,则拒绝原假设(右尾) 如果χ2 ≤ χ2(1-α) 或 χ2 ≥ χ2α,则拒绝原假设(双尾) (如果置信区间不包含σ02,则拒绝原假设) p值法:如果p值≤α,则拒绝原假设 |
临界值法:如果F ≥ Fα,则拒绝原假设(右尾) 如果F ≥ Fα/2,则拒绝原假设(双尾) p值法:如果p值≤α,则拒绝原假设 |
|
|
注:p值法可以显示犯第一类错误的实际概率,而临界值法不能。 |
|||
|
python命令 |
|
1,单样本t检验:scipy.stats.ttest_1samp (a, popmean) 返回:t检验统计量的具体值和相应的p值(双尾) 2,配对t检验:scipy.stats.ttest_rel(a,b) 返回:t检验统计量的具体值和相应的p值(双尾) 3,独立样本t检验: scipy.stats.ttest_ind (a, b, equal_var=True) 或 scipy.stats.ttest_ind_from_stats (mean1, std1,nobs1,mean2, std2,nobs2, equal_var=True) --- 方差相等 scipy.stats.ttest_ind(a, b, equal_var=False) 或 scipy.stats.ttest_ind_from_stats (mean1, std1,nobs1,mean2,std2,nobs2, equal_var=False)--- 方差不相等 返回:t检验统计量的具体值和相应的p值(双尾) |
1,卡方拟合优度检验:scipy.stats.chisquare (f_obs, f_exp=None, ddof=0) 返回:卡方统计量的具体值和相应的p值 2,卡方独立性检验:scipy.stats.chi2_contingency (observed, correction=True) 返回:卡方统计量的具体值,相应的p值,自由度, 期望频率 3,卡方分布检验(比较样本和总体方差): 计算统计量:
|
1,Levene检验:scipy.stats.levene (sample1,sample2,...) 返回:F统计量的具体值和相应的p值 2,单因素方差分析:scipy.stats.f_oneway (sample1,sample2,...) 返回:F统计量的具体值和相应的p值 |