Numpy的基本用法
NumPy(Numerical Python) 是使用python进行机器学习不可或缺的第三方库,它支持数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。ndarray对象是numpy中的基本对象之一,和python列表不同之处在于:python列表可以存放任何类型的元素,而ndarray对象则只能存放相同类型的元素。
python列表中的元素其实是一个指针,指向包含这个python对象所有信息的某个内存位置。由于这里面包含了大量的额外信息,因此python可以自由、动态地编码。但是这些额外信息也会成为负担。当python列表中的元素都是同一类型时,此时如果将数据存储在固定类型的数组中会更高效。python的数组对象提供了数组型数据的有效存储,而numpy则加上了高效的操作。
一. 导入numpy库
import numpy as np
二. 创建numpy数组(numpy array)
1. 从python列表创建(from python lists)
list=[4,5,6,7]
array=np.array(list)
[4 5 6 7]
注意:当使用乘号(*)时,python list做的是复制(replicate),而numpy array做的是乘法(multiply)。
print("list replication:", list*4) print("array multiplication:", array*4)
list replication: [4, 5, 6, 7, 4, 5, 6, 7, 4, 5, 6, 7, 4, 5, 6, 7]
array multiplication: [16 20 24 28]
2. 从python元组创建(from python tuples)
tuple=(1,2,3,4)
array=np.array(tuple)
[1 2 3 4]
3. np.arange([start, ]stop, [step])
array=np.arange(7)
[0 1 2 3 4 5 6]
array=np.arange(7,12)
[ 7 8 9 10 11]
array=np.arange(7,12,2)
[ 7 9 11]
4. np.linspace(start, stop, num_of_elements, endpoint=True)
array=np.linspace(5,15,9)
[ 5. 6.25 7.5 8.75 10. 11.25 12.5 13.75 15. ]
5. np.zeros(shape),np.ones(shape),np.full(shape, num)
array=np.zeros(5)
[0. 0. 0. 0. 0.]
array=np.ones((4,5))
[[1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.]]
array=np.full((3,2),4.4)
[[4.4 4.4] [4.4 4.4] [4.4 4.4]]
6. np.asarray(data) --- 把数据转变成numpy数组格式
7. 使用随机数创建:具体请见下面随机数
三. 查看numpy数组的属性(attributes)
1. size --- 查看numpy array的元素个数
2. shape --- 查看numpy array的形状(每个维度的大小)
3. ndim --- 查看numpy array的维度
4. dtype --- 查看numpy array的元素的数据类型
四. 视图和拷贝(view©)
1. view() --- 仅复制值(a shallow copy: same location, same value, different shape)
2. copy() --- 产生独立拷贝(deep copy: different location)
array=np.arange(12).reshape((3,4))
x=array[:2,::2].copy()
五. 索引(Indexing)和切片(Slicing)
1. array[num] --- 对于一维数组,返回该数组的某个元素;对于多维数组,返回该数组的某一行
2. array[num:] --- 对于一维数组,返回该数组的某个元素以及其之后所有的元素;对于多维数组,返回该数组的某一行以及其之后的所有行
3. array[:num] --- 对于一维数组,返回该数组的某个元素之前的所有元素;对于多维数组,返回该数组的某一行之前的所有行
4. array[row_num, col_num] --- 对于多维数组,返回该数组某一行某一列的元素
5. array[row_num][col_num] --- 对于多维数组,返回该数组某一行某一列的元素
6. array[start:stop:step] --- 对于一维数组,返回该数组中从某一个元素到某一个元素,步长为step
7. array[::-1] --- 返回逆序的数组
8. array[::2] --- 返回数组中每隔一个元素的元素
9. array[row_num:row_num, col_num:col_num] --- 对于多维数组,返回该数组从某一行到某一行,以及从某一列到某一列的元素
注意:索引操作返回的是copy,而切片操作返回的是view(如果此view的数组的值发生改变,那么原数组的值也随之改变)
五. 使用掩码过滤((Mask Arrays)
1. array[mask]
一般在mask里写一些条件,例如:array[array>0],array[array%7==0]。一些条件表示方法:&(和) ,|(或),^(异或),~(非),>(大于),<(小于),==(等于),>=(大于等于),<=(小于等于),!=(不等于)。
(注:and和or用于比较整个对象是否相同,而&和|用于比较每个对象中的内容的比特位是否相同)
六. 广播(Broadcassting)
用于操作不同大小和形状的数组
a1=np.arange(4).reshape((2,2)) a2=np.array([6,7]) array=a1+a2
a1: [[0 1] [2 3]] a2: [6 7] array: [[ 6 8] [ 8 10]]
七. 改变numpy数组的形状
1. reshape(new_shape)
array=np.arange(6).reshape((2,3))
[[0 1 2]
[3 4 5]]
2. ravel() --- 把原数组变成一维数组,返回的是变形后的数组
array=np.arange(6).reshape((2,3)).ravel()
[0 1 2 3 4 5]
3. flatten() --- 把原数组变成一维数组,返回的是数组的拷贝
4. flat --- 把原数组变成一维数组,返回的是数组的迭代器(iterator)
5. array[:, np.newaxis] --- 在原来的数组上增加一个维度(等价于array.reshape((-1,1)))
array=np.arange(4)
x=array[:,np.newaxis]
[[0] [1] [2] [3]]
八. 随机数
1. np.random.randn(dimensions) --- 生成服从标准正态分布的随机数(平均值为0,标准差为1)
array=np.random.randn(4,5)
[[ 2.21603303 -1.64664239 2.45001994 -1.37329856 -0.69289112] [-0.125158 -0.88744257 0.39569274 0.82625695 -1.08780716] [ 0.69045662 -0.37110748 -1.23273598 0.0291697 -1.85835357] [-0.02345338 0.10072476 0.3590989 -0.0499124 -0.46932103]]
2. np.random.uniform(low,high,size) --- 生成服从均匀分布的随机数
array=np.random.uniform(4,5,10)
[4.98608384 4.70541334 4.50306141 4.44011335 4.21199919 4.32929091 4.94769774 4.75963238 4.86165138 4.39888279]
3. np.random.binomial(n trials,p probability of success,size) --- 生成服从二项分布的随机数
array=np.random.binomial(10,0.7,10)
[6 8 9 7 4 7 6 8 9 8]
4. np.random.normal(mean,std,size) --- 生成服从正态分布的随机数
array=np.random.normal(2,4,(4,5))
[[-2.16965713 7.9465455 6.47141735 6.22990766 0.4211604 ] [-6.09374231 6.55291348 3.72097759 1.97147291 -7.87745844] [ 3.52418805 -9.37185049 5.6932117 0.35741766 1.5608389 ] [ 3.98630581 0.30948976 -2.24940441 3.19326126 -8.51553261]]
5. np.random.randint(low,high,size) --- 生成从low(inclusive)到high(exclusive)的随机整数
array=np.random.randint(2,4,10)
[3 3 2 2 2 2 2 2 3 3]
6. np.random.rand(size) --- 生成[0, 1)区间内的随机数
array=np.random.rand(10)
[0.06581389 0.65264403 0.97450565 0.08616934 0.55040952 0.69840924 0.40490815 0.12367222 0.88993262 0.77037247]
7. np.random.choice(array) --- 从一维数组中生成随机样本
array=np.random.rand(10)
num=np.random.choice(array)
0.95955024664668
8. np.random.seed(num) --- 设置随机数种子
9. np.random.RandomState(num) --- 设置随机数种子,是随机数种子的容器
rng=np.random.RandomState(4)
array=rng.rand(10)
[0.96702984 0.54723225 0.97268436 0.71481599 0.69772882 0.2160895 0.97627445 0.00623026 0.25298236 0.43479153]
九. 数学运算
1. +, -, *, / --- 加,减,乘,除
2. // --- 地板除法(取整)
3. % --- 模运算(取余)
4. ** --- 指数运算
5. np.abs() --- 返回绝对值
6. np.exp() --- 返回e的幂次方
7. np.sqrt() --- 返回平方根
8. np.log() --- 返回自然对数(以e为底)
9. np.log2() --- 返回以2为底对数
10. np.log10() --- 返回以10为底对数
11. np.sin() --- 返回正弦
12. np.cos() --- 返回余弦
13. np.std() --- 返回标准差
14. np.var() --- 返回方差
15. np.prod() --- 返回乘积
16. np.sum() --- 返回总和
17. np.mean() --- 返回平均值
18. np.min() --- 返回最小值
19. np.max() --- 返回最大值
20. np.median() --- 返回中位数
十. 合并numpy数组
1. np.concatenate((array1,array2,...), axis=0) --- 按行或列合并数组(数组在合并方向的维度需一致),axis=0表示按行合并,axis=1表示按列合并
a1=np.arange(4).reshape((2,2)) a2=np.array([[6,7]]) array=np.concatenate((a1,a2),axis=0)
[[0 1] [2 3] [6 7]]
2. np.stack((array1,array2,...), axis=0) --- 堆叠数组,增加一个维度
3. np.hstack((array1,array2,...)) --- 相当于按列合并数组
4. np.vstack((array1,array2,...)) --- 相当于按行合并数组
十一. 分隔numpy数组
1. np.split(array, n, axis=0) --- 按行或列将数组均匀分隔成n份,axis=0表示按行分隔,axis=1表示按列分隔
a1=np.array([[6,7],[8,9]])
array=np.split(a1,2)
[array([[6, 7]]), array([[8, 9]])]
2. np.hsplit(array, n) --- 相当于按列分隔数组
3. np.vsplit(array, n) --- 相当于按行分隔数组
十二. 线性代数相关(linear algebra)
1. np.mat(array) --- 将数组转换成矩阵
2. np.dot(a,b) --- 对于一维数组(向量),计算这两个数组的点积,对于多维数组(矩阵),运行矩阵乘法
3. np.outer(a,b) --- 计算两个向量的外积
4. np.eye(num) --- 创建一个num*num的单位矩阵(identity matrix)
5. np.linalg.solve(“Coefficient” matrix, y) --- 求解线性方程组
6. np.linalg.eig(matrix) --- 求矩阵的特征值,特征向量
7. np.linalg.lstsq(“Coefficient” matrix, y) --- 返回线性矩阵用最小二乘法获得的解
8. np.linalg.det(matrix) ---矩阵求行列式
9. np.linalg.inv(matrix) --- 矩阵求逆
10. np.linalg.norm(array) --- 求范数
11. np.trace(array) --- 求矩阵的迹(对角线元素的和)
12. np.diag(matrix) --- 返回矩阵的对角线元素
13. np.linalg.svd(array) --- 奇异值分解
十三. 其他
1. np.argmax(array) --- 返回最大值的索引
2. np.argmin(array) --- 返回最小值的索引
3. np.any(array, axis=None) --- 测试数组(按行或按列)中的任意一个元素是否为真
4. np.all(array, axis=None) --- 测试数组(按行或按列)中的所有元素是否都为真
5. np.meshgrid(x,y) --- 生成网格点坐标矩阵
x=np.arange(4) y=np.arange(4,7) X,Y=np.meshgrid(x,y)
x: [0 1 2 3]
y: [4 5 6]
X: [[0 1 2 3] [0 1 2 3] [0 1 2 3]] Y: [[4 4 4 4] [5 5 5 5] [6 6 6 6]]
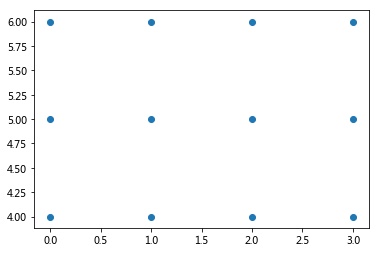
X,Y = meshgrid(x,y) :将向量x和y定义的区域转换成矩阵X和Y,其中矩阵X的行向量是向量x的简单复制,而矩阵Y的列向量是向量y的简单复制。假设x是长度为m的向量,y是长度为n的向量,则最终生成的矩阵X和Y的维度都是 n*m 。
6. astype(dtype) --- 转换数据类型
7. np.where(condition, x, y) --- 如果满足条件(condition),输出x,不满足则输出y
8. np.count_nonzero(array) --- 统计数组中非零值的个数
9. np.sort(array) --- 返回排好序的数组,默认的排序算法为快速排序
10. np.argsort(array) --- 返回原始数组排好序的索引值
11. np.partition(array, k) --- 找出数组中第k小的值,输出一个新数组,最左边是第k小的值,往右是任意顺序的其他值
12. np.argpartition(array, k) --- 找出数组中第k小的值的索引,输出一个新数组,最左边是第k小的值的索引,往右是任意顺序的其他值的索引
13. np.percentitle(array, percentile, axis=None) --- 返回数组百分比分位数
array=np.array([[6,7],[8,9]])
x=np.percentile(array,60,axis=0)
[7.2 8.2]



