皮尔逊相关系数（Pearson Correlation Coefficient，Pearson's r）
Pearson's r，称为皮尔逊相关系数（Pearson correlation coefficient），用来反映两个随机变量之间的线性相关程度。
用于总体（population）时记作ρ (rho)（population correlation coefficient）：
给定两个随机变量X,Y，ρ的公式为：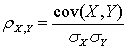 
其中： cov(X,Y)是X，Y的协方差
σX是X的标准差
σY是Y的标准差
用于样本（sample）时记作r（sample correlation coefficient）：
给定两个随机变量X,Y，r的公式为：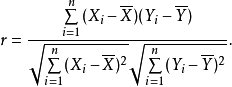
其中： n是样本数量
Xi, Yi是变量X，Y对应的i点观测值
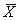是X样本平均数，
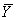是Y样本平均数
r的取值在-1与1之间。取值为1时，表示两个随机变量之间呈完全正相关关系；取值为-1时，表示两个随机变量之间呈完全负相关关系；取值为0时，表示两个随机变量之间线性无关。
那么r值需要多大才说明两变量之间有显著关联呢？我们用样本相关系数r作为总体相关系数ρ的估计值，要判断r值确实显著，而不是由于抽样误差或偶然因素导致其显著，需要进行假设检验。可以用scipy来计算r并做假设检验：
scipy.stats.pearsonr(x, y)
那么皮尔逊相关系数是怎么得来的呢？（参考：https://blog.csdn.net/ichuzhen/article/details/79535226）
要理解皮尔逊相关系数，首先要理解协方差（Covariance）
。协方差可以反映两个随机变量之间的关系，如果一个变量跟随着另一个变量一起变大或者变小，那么这两个变量的协方差就是正值，就表示这两个变量之间呈正相关关系，反之相反。样本协方差的公式如下：
。
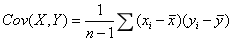如果协方差的值是个很大的正数，我们可以得到两个可能的结论：
（1） 两个变量之间呈很强的正相关性
（2） 两个变量之间并没有很强的正相关性，协方差的值很大是因为X或Y的标准差很大
那么到底哪个结论正确呢？只要把X和Y变量的标准差，从协方差中剔除不就知道了吗？协方差能告诉我们两个随机变量之间的关系，但是却没法衡量变量之间相关性的强弱。因此，为了更好地度量两个随机变量之间的相关程度，引入了皮尔逊相关系数。可以看到，皮尔逊相关系数就是用协方差除以两个变量的标准差得到的。
