ZROI 白银御行

ZROI 白银御行

本题的男点大概在如何批量的计算两个矩阵有交。

设一个矩阵的四个端点为 \(A,B,C,D\)，↖，↗，↙，\(↘\)

对于一个矩阵 X，另一个矩阵 Y 和它有交，首先要满足 Y 的 A 在 X 的 D 左上方，

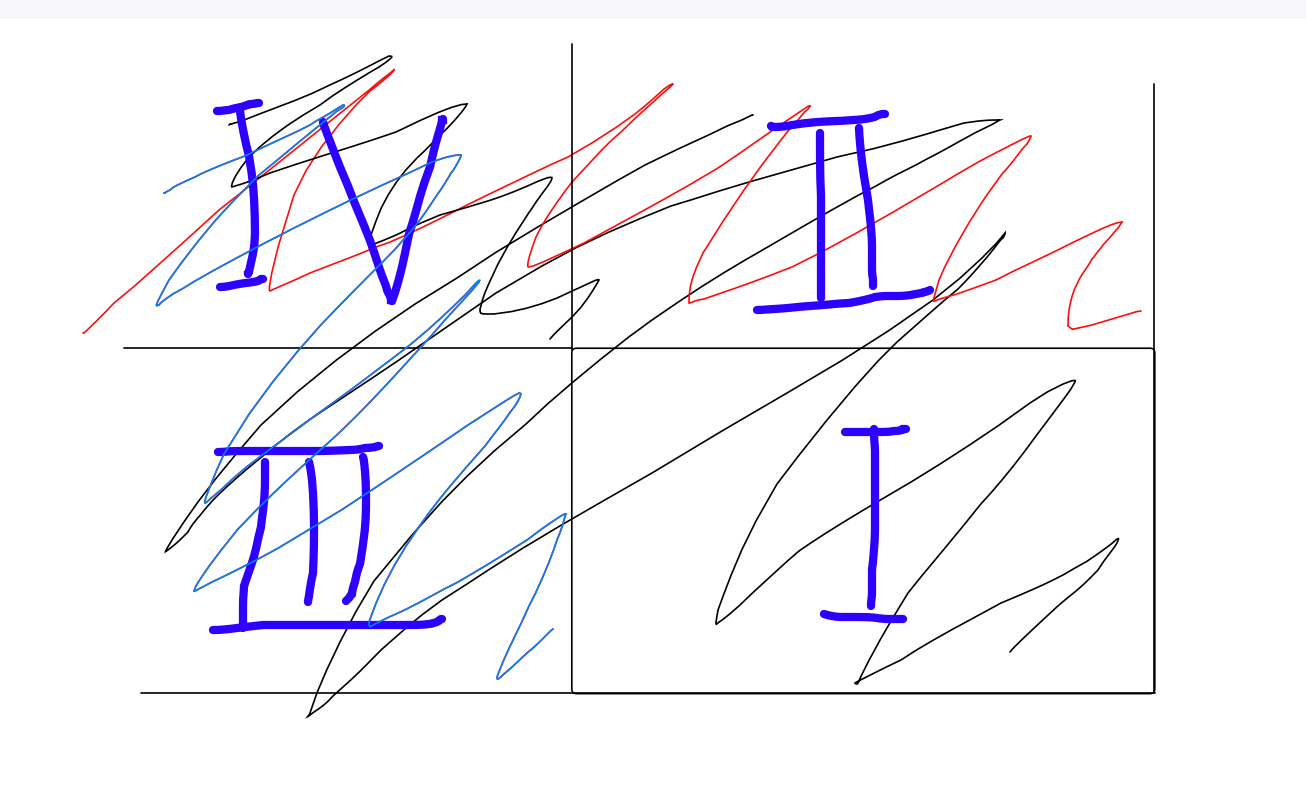
如图所示的四个区域，对于第 1 个区域已无问题。第二区发现如果 C 点在 1 内则有，否则无，无的情况正好是 \(Y_C < X_B\)，第三个区域同理，这时候在四区域内的被减了两遍，再加上这种情况即可。

细节可以手玩一下。更一般的想，Y 这个矩形的上边界一定要比 X 下边界高，左边界要比 X 右边界靠左。

所以式子就是

\[[Ry_1 \le Rx_2][Cy_1 \le Cx_2][Ry_2 \ge Rx_1][Cy_2 \ge Cx_1]\\ = [Ry_1 \le Rx_2][Cy_1 \le Cx_2] - [Ry_1 \le Rx_2][Cy_1 \le Cx_2][Ry_2 < Rx_1]\\ - [Ry_1 \le Rx_2][Cy_1 \le Cx_2][Cy_2 < Cx_1] + [Ry_1 \le Rx_2][Cy_1 \le Cx_2][Ry_2 < Rx_1][Cy_2 < Cx_1]\\ = [Ry_1 \le Rx_2][Cy_1 \le Cx_2] - [Cy_1 \le Cx_2][Ry_2 < Rx_1]\\ - [Ry_1 \le Rx_2][Cy_2 < Cx_1] + [Ry_2 < Rx_1][Cy_2 < Cx_1] \]

这样也可以很方便的拓展到高维上。