后缀自动机感性理解
后缀自动机感性理解
Update on 2020/9/16: 修复和部分排版问题和内容
后缀自动机实是不是很好理解,尤其是直接看大段的证明,不知道它在干什么,可能会有点懵
那我先介绍一下我的感性理解好了,大家看这篇文章可能会更好的理解其他人的博客 QAQ
前置芝士:trie 树
先来讲一下假后缀树 ($ n^2 $) ,由于它是假的所以很容易理解, 不用怕
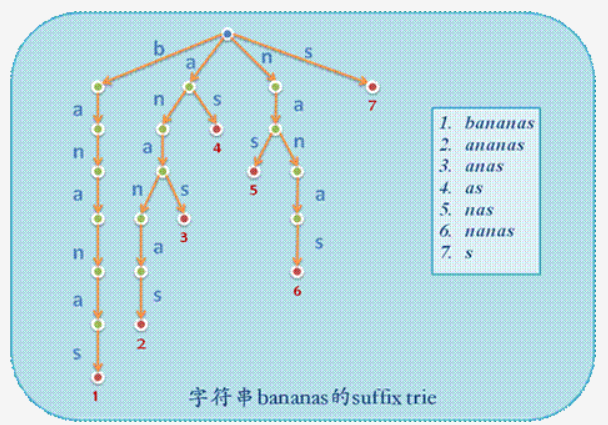
对于一个字符串(例: \(bananas\))来说, 把它的所有后缀($bananas, ananas, nanas, anas, nas, as, s $) 一个一个的插入 \(trie\) 树,并在末尾打上 \(end\) 标记, 就是暴力的后缀 \(trie\) 了,显然时空复杂度均为 \(O(n^2)\)
那么可以说后缀自动机是对它很大程度上的优化了,也就是对重复出现的子串和后缀进行压缩等操作,使时空复杂度骤降为 \(O(n)\),并具有后缀树的一些性质
关于子串的理解: 对于字符串 \(S\) 的一个子串, 你可以理解它为((\(S\) 的一个后缀)的前缀)
也就是如果 \(S\) 的一个子串在 \(trie\) 上一定是一条从根节点开始的路径
有啥用呢
- 找一个子串的出现次数:在 \(trie\)上找到它的路径,在它下方的 \(end\) 标记个数,也就是它是多少个后缀的前缀
- 找一个子串第一次(最后一次)出现位置,就是向下走到深度最大(深度最小)的 \(end\) 标记
- 统计本质不同子串的个数, 即 \(trie\) 树上节点的个数
开始切入后缀自动机
后缀自动机神奇的连了一大堆边,成功的压缩了空间与时间
他有一个小性质:从始节点开始,走任意路径,到终止节点的路径均是原字符串的一个后缀,终止节点可能不止一个
先贴一张图,来自 zjp大佬的博客,方便理解性质:
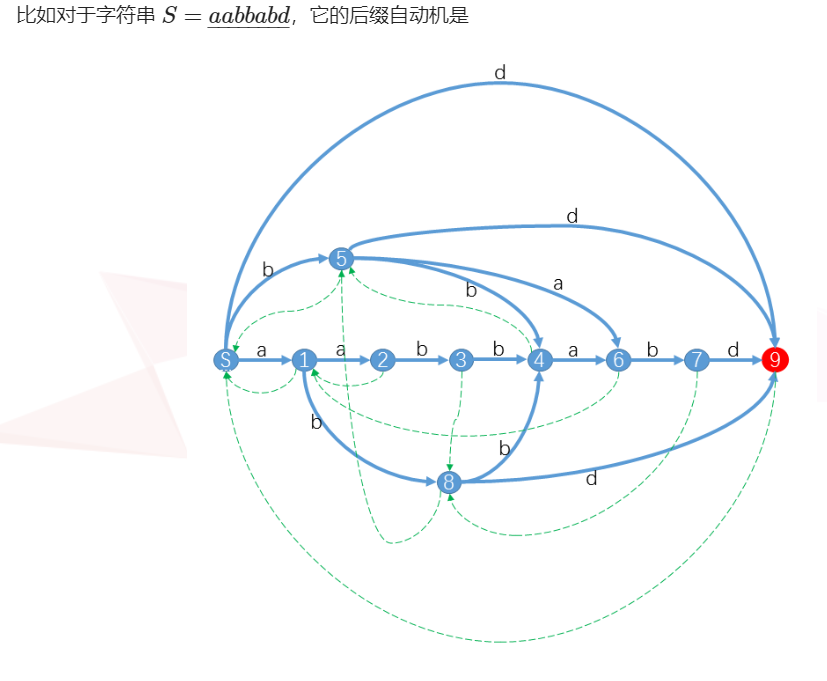
几个必备要素:
endpos(x):它是一个集合, 表示一个子串的所有结束位置(可能有许多结束位置,因为会有本质相同子串),如果两个子串的 \(endpos\) 相同, 那么这两个子串属于一个“状态” ,同时他俩一个是另一个的后缀
len(x):对于一个状态所表示的一堆字符串,他们最长的那个的长度称为 \(len(x)\),同时这些字符串按长度排个序,容易发现长度是连续的整数
后缀 \(link\):
设一个 \(A\) 状态如 ("abab", "bab", "ab") 那么 "b" 就是状态中没有的最长后缀,即 "abab","bab", "ab" (在 \(endpos\) 集合里的串)的最长的且没有在该状态出现的后缀
那么我将 \(A\) 状态向 "b" 状态所在的 \(B\) 状态连有向边,叫做 \(link\) , 如果从一个状态不断的跳 \(link\) ,那么就会遍历一个字符串的所有后缀
转移函数:
在一个状态内所有字符串的末尾加一个字符使它变成另一个状态,如 ("aba","caba",ccaba")+ 'c' = (“abac","cabac","ccabac")
设 \(ch[s]['a'-'z']\) 为转移函数, 如 \(ch[s]['a']\) 表示从 \(s\) 状态加一个 'a' 字符转移到哪个状态
下面来讲构造:
考虑从前往后一个一个加入字符,即增量法,这样就保证了每加一个字符都满足后缀自动机的性质
设当前最长串为 \(S[1\dots i-1]\), 现在加一个字符 \(S[i]\),我们要干的事就是让它的所有后缀都能用一条从起点到终止节点的路径表示出来,那么假设 \(S[1\dots i-1]\) 的后缀自动机已经构造好了,满足所有的后缀都可以表出,那么让我们让原先所有的路径(所有的后缀)末尾加一个字符不就行了?上面介绍了 转移函数,用转移函数不就行了?当然用转移函数是必要的,但还有些细节要考虑,比如集合里的串出现次数不一样了怎么办和一个 \(endpos\) 集合 \(A\) 已经有了转移函数 \(ch[A][c]\),再要设定一个指向 \(c\) 的函数又该怎么办呢,覆盖肯定是不行的。下面我们来讨论如何解决这些问题。
首先 \(S[1...i]\) 肯定是一个新状态,因为它是所有子串中最长的串,设这个状态为 \(np\)
因为前面 \(S[1...i-1]\) 已经构造好了,我们从状态 \(p = {s[1...i-1]}\) 开始跳 后缀 \(link\),如果没有 转移函数 \(ch[p][c]\),这说明 \(S[1\dots i-1]\) 没有 \(p\) 集合中子串加上 \(c\) 形成的新子串,那么直接让 \(ch[p][c]=np\) 即可,因为 \(np\) 集合中的子串都只出现一次。
for (; p && !ch[p][c]; p = f[p]) ch[p][c] = np;
if (!p) f[np] = 1;
那如果碰到了 \(ch[A][c] = q(q \not= 0\)) 怎么办呢,我们分两种情况
如果 \(len(q) = len(p) + 1\),这时你发现 \(q\) 集合和其 后缀 link 中的所有字符串正好是 \(np\) 剩下要组成的全部后缀,所以我们直接利用 \(q\),让 \(q\) 成为下一个终止状态,\(np\) 向 \(q\) \(link\) 一下即可。
否则,原先 \(q\) 中的字符串集就不再有相同的 \(endpos\),因为从 \(np\) 转移过来的串也是 \(S[1...n]\) 的后缀,所以这部分\(endpos\) 会多一个 \((i)\),这个状态就会分裂,因此我们新建一个状态 \(nq\),原先的 \(q\) 变为了 \(q\) 和 \(nq\),\(nq\) 要保证 \(len(nq) = len(p) + 1\),可以感性的想象为把字符串集合横着劈开了,这样我们就又转化为上一种情况了,具体来说还要改变 \(q\) 的 后缀 link 为 \(nq\),\(nq\) 的 转移函数 继承于 \(q\),所有指向 \(q\) 的 转移函数 要改到 \(nq\) 上。
可以看看图理解一下,来源于神仙 \(zjp\)
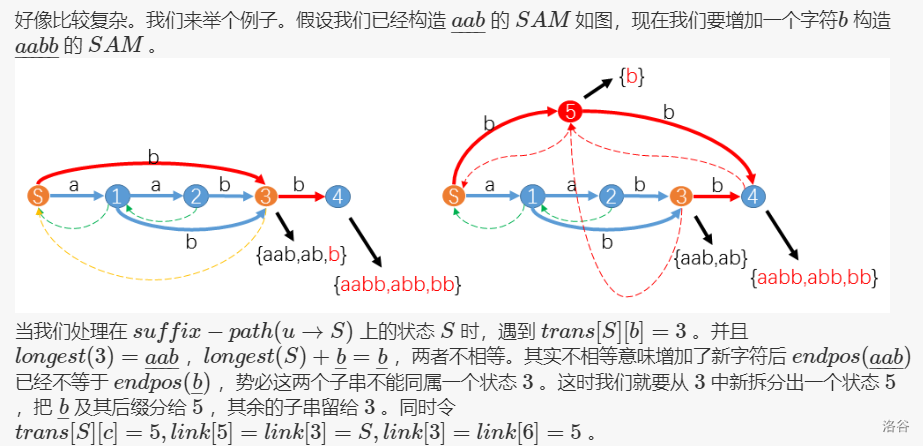
代码:
void add(int c) {
int p = las, np = las = ++cnt; zhi[cnt] = 1;
len[np] = len[p] + 1;
for (; p && !ch[p][c]; p = f[p]) ch[p][c] = np;
if (!p) f[np] = 1;
else {
int q = ch[p][c];
if (len[q] == len[p] + 1) f[np] = q;
else {
int nq = ++cnt;
for (int i = 0;i < 26; i++)
ch[nq][i] = ch[q][i];
len[nq] = len[p] + 1, f[nq] = f[q];
f[q] = f[np] = nq;
for (; p && ch[p][c] == q;p = f[p]) ch[p][c] = nq;
}
}
}

