CRC校验
CRC校验原理：
在k位信息码后再拼接r位的校验码，报文编码长度为n位，因此，这种编码又叫（n，k）码。
定理：对于一个给定的（n，k）码，可以证明,存在一个最高次幂为n=k+r的多项式G(x)，存在且仅存在一个R次多项式G(x)，使得
。
其中:
m(x) ：k次信息多项式，
r(x) ：r-1次校验多项式，
g(x)：生成多项式：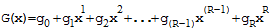
。
发送方通过指定的G(x)产生r位的CRC校验码，接收方则通过该G(x)来验证收到的报文码的CRC校验码是否为0。
假设发送信息用信息多项式C(X)表示，将C(x)左移r位，则可表示成C(x)*2r，这样C(x)的右边就会空出r位校验码的位置，做除法（模2除）
，得到的余数R就是校验码。发送的CRC编码是
,验证接收到的报文编码是否至正确，依然是做模2除：
。
CRC校验手算示例：
生成多项式:G(X)=X4+X3+1，要求出二进制序列10110011的CRC校验码。
（1）G(X)=X4+X3+1,二进制比特串为11001;(有X的几次方，对应的2的几次方的位就是1)
（2）因为校验码4位，所以10110011后面再加4个0，得到101100110000，用“模2除法”(其实就是亦或^)即可得出结果；
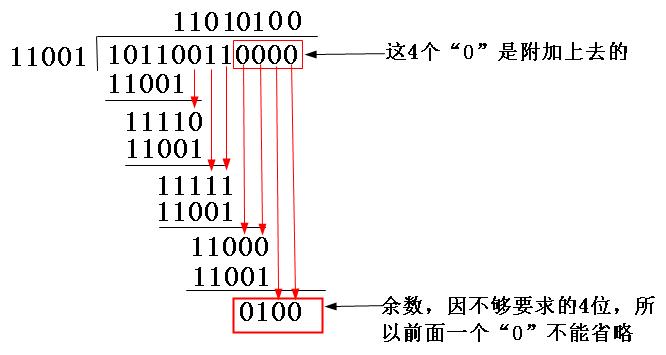
图5-10 CRC校验码计算示例
（3）CRC^101100110000得到101100110100。发送到接收端；
（4）接收端收到101100110100后除以11001(以“模2除法”方式去除),余数为0则无差错；
