二分图最大匹配,匈牙利算法
关于二分图匹配的一些知识:
匹配:选取一些边,使得任意两条边没有公共点(每个点至
多属于一条边)
最大匹配:选取边数尽可能多
完美匹配:所有点都在匹配中(每个点恰好属于一条边)
匹配边:选中的边
非匹配边:没有选中的边
匹配点:和选中边相连的点
非匹配点:和选中边不相连的点
匈牙利算法:
匈牙利算法的算法核心是寻找增广路径,每找到一条增广路径都能使答案加一。
增广路径:
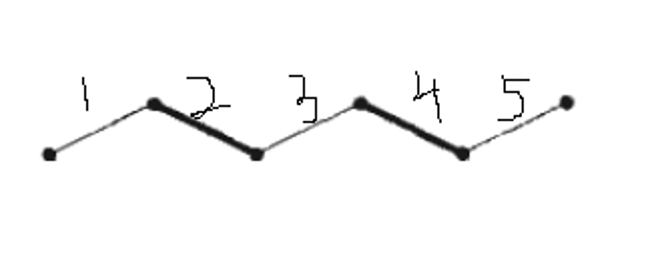
可以用1,3,5代替2,4,这样的路径称为增广路径。
算法流程:
从左侧集合中的第一个点开始寻找匹配
如果某条边的中点没有被匹配过就匹配上,否则就寻找是否存在增广路径。
寻找增广路径的过程其实是一个再匹配的过程,让已经配对的左集合端点暂时取消匹配而去找下一个能匹配的右集合端点
如果能找到就存在增广路径,否则不存在。
匹配部分代码
1 inline bool dfs(int pos) 2 { 3 for(int i=first[pos];i;i=edge[i].nxt) 4 { 5 int e=edge[i].ed; 6 if(!used[e]) 7 { 8 used[e]=true; 9 if(!match[e]||dfs(e)) 10 { 11 match[e]=pos; 12 return true; 13 } 14 } 15 } 16 }
匈牙利算法代码
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 #define maxn 2005 6 7 using namespace std; 8 9 struct node 10 { 11 int ed,nxt; 12 }; 13 node edge[maxn*maxn]; 14 int n,m,e,first[maxn],ans,cnt; 15 bool used[maxn]; 16 int match[maxn]; 17 18 inline void add_edge(int st,int ed) 19 { 20 cnt++; 21 edge[cnt].ed=ed; 22 edge[cnt].nxt=first[st]; 23 first[st]=cnt; 24 return; 25 } 26 27 inline bool dfs(int k) 28 { 29 for(int i=first[k];i!=0;i=edge[i].nxt) 30 { 31 int e=edge[i].ed; 32 if(!used[e]) 33 { 34 used[e]=true; 35 if(!match[e]||dfs(match[e])) 36 { 37 match[e]=k; 38 return true; 39 } 40 } 41 } 42 return false; 43 } 44 45 int main() 46 { 47 scanf("%d%d%d",&n,&m,&e); 48 for(int i=1;i<=e;i++) 49 { 50 int st,ed; 51 scanf("%d%d",&st,&ed); 52 if(st<=n&&ed<=m) add_edge(st,ed); 53 } 54 for(int i=1;i<=n;i++) 55 { 56 memset(used,false,sizeof(used)); 57 if(dfs(i)) ans++; 58 } 59 printf("%d",ans); 60 return 0; 61 }

