哈夫曼编码
离开了校园,连手机流量都要省着用,然后突发奇想的思考如何才能节省传输大小
1. 哈夫曼树
构建最短带权路径长度的二叉树,叫做哈夫曼树,也叫最优树(权重越大的结点离树根越近)
1.1 基本定义
- 路径:树中的一个节点到另一个节点之间的通路
- 路径长度:某路径中所经过的节点数量
- 节点的权:给节点赋值,这个值称为节点的权
- 节点的带权路径长度:根节点到某节点的路径长度 * 该节点的权
- 树的带权路径长度:树中所有叶子节点的带权路径长度之和,记作 "WPL"
1.2 构建步骤
- 选出两个最小权值作为左右子树,新建其父节点(虚线),权值为左右子树权值之和
- 从权值队列中删除第一步的左右子树的权值,添加第一步新增的二叉树到权值队列
- 重复第一、二步,直到构建完权值队列中所有节点
1.3 构建图示

WPL:9 * 1 + 6 * 2 + 4 * 3 + 1 * 3 = 36
2. 哈夫曼编码
哈夫曼编码是一种编码方式,其可以对信息进行压缩,而从提高存储,传输的效率
2.1 基本定义
- 等长编码:任何字符的编码长度都相同,比如ASCII。虽读写方便,但浪费资源,且有前缀码问题
- 无前缀编码:任一个编码都不是其他任何编码的前缀。[01,10,11,100,101]中10是100的前缀,因此不是无前缀编码
2.2 构建步骤
- 根据权值构建哈夫曼树
- 将哈夫曼树的左树标 0,右树标记1,根节点不计算
- 将权值替换为对应的字符
- 列出字符对应的二进制
2.3 构建图示
假设字符A、B、C、D对应的权值为1、9、4、6
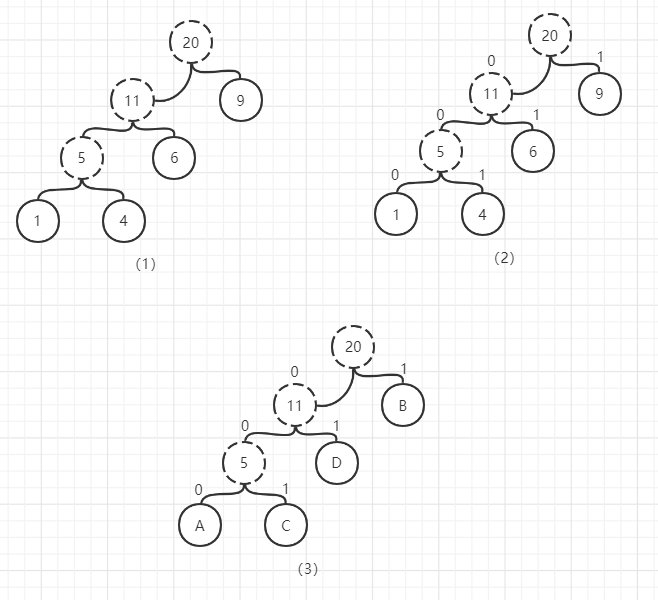
(4)
| 字符 | 编码 |
|---|---|
| A | 000 |
| B | 1 |
| C | 001 |
| D | 01 |
2.4 哈夫曼编码应用
通过哈夫曼编码传输文本、图片,查看前后对比
2.4.1 哈夫曼编码 java 实现
/**
* @author Howl
* 哈夫曼编码
*/
public class HuffmanCode {
/**
* 哈夫曼树结点结构
*/
private static class Node implements Comparable<Node> {
/**
* 权值、二进制编码0、1、左右孩子
*/
int weight;
String code;
Node left;
Node right;
Node(int weight) {
this.weight = weight;
}
Node(int weight, Node left, Node right) {
this.weight = weight;
this.left = left;
this.right = right;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.weight, o.weight);
}
}
/**
* 根节点、存储全部节点
*/
private Node root;
private static Node[] nodes;
/**
* 构建哈夫曼树
* 建树是从最小权值开始的,所以借助小根堆
*/
public void createHuffman(int[] weights) {
// 构建小根堆,弹出是最小的元素
Queue<Node> nodeQueue = new PriorityQueue<>();
nodes = new Node[weights.length];
for (int i = 0; i < weights.length; i++) {
nodes[i] = new Node(weights[i]);
nodeQueue.add(nodes[i]);
}
// 节点队列只剩一个节点结束,即根节点构建完成
while (nodeQueue.size() > 1) {
// 弹出权值最小的两个结点
Node left = nodeQueue.poll();
Node right = nodeQueue.poll();
// 创建新节点作为两结点的父节点
Node parent = new Node(left.weight + right.weight, left, right);
nodeQueue.add(parent);
}
// 哈夫曼树根,遍历要用,优先级队列GC
root = nodeQueue.poll();
// 实现编码
encode();
}
/**
* 输入字符下标,输出对应的哈夫曼编码
*/
public String convertHuffmanCode(int index) {
return nodes[index].code;
}
/**
* 递归填充二进制编码
*/
private void encode() {
encode(root, "");
}
private void encode(Node node, String code) {
if (node == null) {
return;
}
node.code = code;
encode(node.left, node.code + "0");
encode(node.right, node.code + "1");
}
/**
* 测试
*/
public static void main(String[] args) {
// 字符及其对应权值
char[] chars = {'A', 'B', 'C', 'D', 'E', 'F'};
int[] weights = {2, 3, 7, 9, 18, 25};
HuffmanCode huffManCode = new HuffmanCode();
huffManCode.createHuffman(weights);
for (int i = 0; i < chars.length; i++) {
System.out.println(chars[i] + ":" + huffManCode.convertHuffmanCode(i));
}
}
}
2.4.2 传输实现
- 将原文进行哈夫曼编码,记录字符及其对应的编码,保存文件为 HuffmanCode
- 将原文的字符用哈夫曼编码代替,保存文件为 HuffmanText
- 将上面两个文件发送给对方
- 对方根据这两份文件就可以解码出原文
3. 开源压缩框架
3.1 图片
Thumbnailator是专门压缩图片的,使用非常简洁
// 图片压缩
Thumbnails.of("C:\\Users\\Howl\\Desktop\\InPic.png") // 输入图片地址
.scale(1) // 和原尺寸大小,即长度,1是原大小
.outputQuality(0.5) // 和原图的质量
.outputFormat("jpg") // 输出格式,png为高保真不会压缩
.toFile("C:\\Users\\Howl\\Desktop\\OutPic"); // 输出地址
}
参考:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号



