B-+树
B-树
B树是二叉平衡树的升级版,可以多路自平衡,而且属于外查找,即数据是放在外存之中的,这时候就要考虑 IO 操作优化了,相比二叉查找树他们的时间复杂度都是O(log N),优势在于B树的深度相比小很多,在数据很大的情况下从磁盘读取次数小了,加快了查找速度,所以B树及其同类经常用在文件系统或数据库中,下面先来说一下B树
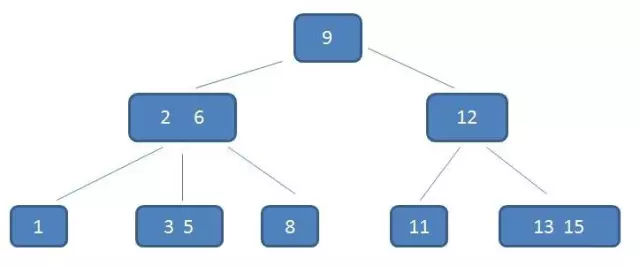
- B树的节点中含有孩子的最大值称为该树的阶,通常用m表示,
(m >= 2) - 若根节点不是叶子结点,则根节点最少有两颗子树
- 树中每个中间结点都包含k-1个元素和k个孩子,
ceil(m/2) <= k <= m - 树中叶子节点都包含k-1个元素,
ceil(m/2) <= k <= m - 所有的叶子结点都位于同一层
B+树
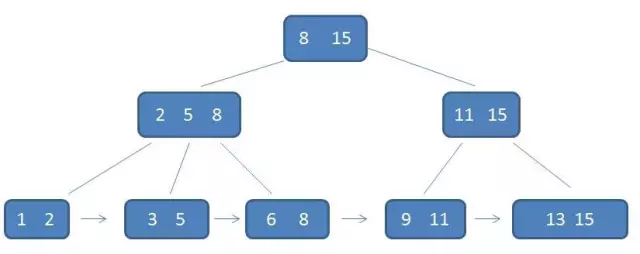
B+树又是B-树的升级版,一颗m阶的B+树,在B-树的前提下又有下面的区别:
-
根节点的最大元素是整棵树的最大元素
-
中间节点有多少个孩子,就有多少个元素(元素不保存数据了,只用于索引,所有数据都存在叶子节点中)
-
所有中间结点的元素都同时存在于子节点上,且在子节点元素中是最大(最小)元素
-
所有叶子节点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子节点按照关键字组成链表
二者区别
- B+树中只有叶子节点才有指向数据记录的存储地址,B-树的节点则都有
- B+树因为中间元素没有数据记录的存储地址,同样的磁盘页可以存储更多节点元素(即同样元素,B+树更矮,IO次数更少)
- B+树单查询必须查到叶子节点,因为叶子才有数据记录的存储地址,而B-树则查到就返回,不稳定
- B+树范围查询只需在叶子节点遍历链表即可,而B-树需要中序遍历才能确定范围




 浙公网安备 33010602011771号
浙公网安备 33010602011771号



